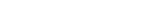bessel_Jx

Evaluates a sequence of Bessel functions of the first kind with real order and complex arguments.

Synopsis

#include <imsl.h>

f_complex *imsl_c_bessel_Jx (float xnu, f_complex z, int n, …, 0)

The type d_complex function is imsl_z_bessel_Jx.

Required Arguments

float xnu (Input)
The lowest order desired. The argument xnu must be greater than −1/2.

f_complex z (Input)
Argument for which the sequence of Bessel functions is to be evaluated.

int n (Input)
Number of elements in the sequence.

Return Value

A pointer to the n values of the function through the series. Element i contains the value of the Bessel function of order xnu + i for i = 0, …, n − 1.

Synopsis with Optional Arguments

#include <imsl.h>

f_complex *imsl_c_bessel_Jx (float xnu, f_complex z, int n,

IMSL_RETURN_USER, f_complex bessel[],

0)

Optional Arguments

IMSL_RETURN_USER, f_complex bessel[] (Output)
Store the sequence of Bessel functions in the user-provided array bessel[].

Description

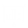
The Bessel function Jv(z) is defined to be

 

This function is based on the code BESSCC of Barnett (1981) and Thompson and Barnett (1987). This code computes Jv(z) from the modified Bessel function Iv(z), using the following relation, with ρ = eip/2:

 

Example

In this example, J0.3+n-1 (1.2 + 0.5i), ν = 1, …, 4 is computed and printed.

 

#include <imsl.h>

#include <stdio.h>

 

int main()

{

int n = 4;

int i;

float xnu = 0.3;

static f_complex z = {1.2, 0.5};

f_complex *sequence;

 

sequence = imsl_c_bessel_Jx(xnu, z, n, 0);

 

for (i = 0; i < n; i++)

printf("I sub %4.2f ((%4.2f,%4.2f)) = (%5.3f,%5.3f)\n",

xnu+i, z.re, z.im, sequence[i].re, sequence[i].im);

}

Output

 

I sub 0.30 ((1.20,0.50)) =(0.774,-0.107)

I sub 1.30 ((1.20,0.50)) =(0.400,0.159)

I sub 2.30 ((1.20,0.50)) =(0.087,0.092)

I sub 3.30 ((1.20,0.50)) =(0.008,0.024)

 

Fatal Errors

IMSL_BESSEL_CONT_FRAC

Continued fractions have failed to converge. The double precision version of this function provides the most accurate solution.