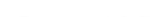bivariate_normal_cdf

Evaluates the bivariate normal distribution function.

Synopsis

#include <imsl.h>

float imsl_f_bivariate_normal_cdf (float x, float y, float rho)

The type double function is imsl_d_bivariate_normal_cdf.

Required Arguments

float x (Input)
The x-coordinate of the point for which the bivariate normal distribution function is to be evaluated.

float y (Input)
The y-coordinate of the point for which the bivariate normal distribution function is to be evaluated.

float rho (Input)
Correlation coefficient.

Return Value

The probability that a bivariate normal random variable with correlation rho takes a value less than or equal to x and less than or equal to y.

Description

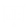
Function imsl_f_bivariate_normal_cdf evaluates the distribution function F of a bivariate normal distribution with means of zero, variances of one, and correlation of rho; that is, with ρ =rho, and ∣ρ∣ < 1,

 

To determine the probability that U ≤u0 and V ≤v0, where (U, V)T is a bivariate normal random variable with mean μ =(μU, μV)T and variance-covariance matrix

 

transform (U, V)T to a vector with zero means and unit variances. The input to imsl_f_bivariate_normal_cdf would be X =(u0 - μU)/σU, Y =(v0 - μV)/σV, and ρ =σUV/(σUσV).

Function imsl_f_bivariate_normal_cdf uses the method of Owen (1962, 1965). Computation of Owen’s T-function is based on code by M. Patefield and D. Tandy (2000). For ∣ρ∣ =1, the distribution function is computed based on the univariate statistic, Z =min(x, y), and on the normal distribution function imsl_f_normal_cdf, which can be found in Chapter 11 of the IMSL C Numerical Stat Library, “Probablility Distribution Functions and Inverses.”

Example

Suppose (X, Y) is a bivariate normal random variable with mean (0, 0) and variance-covariance matrix

 

This example finds the probability that X is less than −2.0 and Y is less than 0.0.

 

#include <imsl.h>

#include <stdio.h>

 

int main()

{

float p, rho, x, y;

 

x = -2.0;

y = 0.0;

rho = 0.9;

p = imsl_f_bivariate_normal_cdf(x, y, rho);

printf(" The probability that X is less than -2.0"

" and Y is less than 0.0 is %6.4f\n", p);

}

Output

 

The probability that X is less than -2.0 and Y is less than 0.0 is 0.0228