int_fcn_qmc
Integrates a function on a hyper-rectangle using a quasi-Monte Carlo method.
Synopsis
#include <imsl.h>
float imsl_f_int_fcn_qmc (float fcn(), int ndim, float a[], float b[], …, 0)
The type double function is imsl_d_int_fcn_qmc.
Required Arguments
float fcn (int ndim, float x[]) (Input)
User-supplied function to be integrated.
int ndim (Input)
The dimension of the hyper-rectangle.
float a[] (Input)
Lower limits of integration.
float b[] (Input)
Upper limits of integration.
Return Value
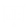
The value of
is returned. If no value can be computed, then NaN is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_int_fcn_qmc (float fcn(), int ndim, float a[], float b[],
IMSL_ERR_ABS, float err_abs,
IMSL_ERR_REL, float err_rel,
IMSL_ERR_EST, float *err_est,
IMSL_MAX_EVALS, int max_evals,
IMSL_BASE, int base,
IMSL_SKIP, int skip,
IMSL_FCN_W_DATA, float fcn(), void *data,
0)
Optional Arguments
IMSL_ERR_ABS, float err_abs (Input)
Absolute accuracy desired.
Default: err_abs = 1.0e-4.
IMSL_ERR_REL, float err_rel (Input)
Relative accuracy desired.
Default: err_rel = 1.0e-4.
IMSL_ERR_EST, float *err_est (Output)
Address to store an estimate of the absolute value of the error.
IMSL_MAX_EVALS, int max_evals (Input)
Number of evaluations allowed.
Default: No limit.
IMSL_BASE, int base (Input)
The value of IMSL_BASE used to compute the Faure sequence.
IMSL_SKIP, int skip (Input)
The value of IMSL_SKIP used to compute the Faure sequence.
IMSL_FCN_W_DATA, float fcn (int ndim, float x[], void *data), void *data (Input)
User supplied function to be integrated, which also accepts a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See Passing Data to User-Supplied Functions in the introduction to this manual for more details.
Description
Integration of functions over hypercubes by direct methods, such as imsl_f_fcn_hyper_rect, is practical only for fairly low dimensional hypercubes. This is because the amount of work required increases exponential as the dimension increases.
An alternative to direct methods is Monte Carlo, in which the integral is evaluated as the value of the function averaged over a sequence of randomly chosen points. Under mild assumptions on the function, this method will converge like 1/n1/2, where n is the number of points at which the function is evaluated.
It is possible to improve on the performance of Monte Carlo by carefully choosing the points at which the function is to be evaluated. Randomly distributed points tend to be non-uniformly distributed. The alternative to at sequence of random points is a low-discrepancy sequence. A low-discrepancy sequence is one that is highly uniform.
This function is based on the low-discrepancy Faure sequence as computed by imsl_f_faure_next_point (see Chapter 10, “Statistics and Random Number Generation”).
On some platforms, imsl_f_int_fcn_qmc can evaluate the user-supplied function fcn in parallel. This is done only if the function imsl_omp_options is called to flag user-defined functions as thread-safe. A function is thread-safe if there are no dependencies between calls. Such dependencies are usually the result of writing to global or static variables.
Example
#include <imsl.h>
#include <stdio.h>
#include <math.h>
float fcn(int ndim, float x[]);
int main()
{
int k, ndim = 10;
float q, a[10], b[10];
for (k = 0; k < ndim; k++) {
a[k] = 0.0;
b[k] = 1.0;
}
q = imsl_f_int_fcn_qmc (fcn, ndim, a, b,
0);
printf ("integral=%10.3f\n", q);
}
float fcn (int ndim, float x[])
{
int i, j;
float prod, sum = 0.0, sign = -1.0;
for (i = 0; i < ndim; i++) {
prod = 1.0;
for (j = 0; j <= i; j++) {
prod *= x[j];
}
sum += sign * prod;
sign = -sign;
}
return sum;
}
Output
q = -0.333
Fatal Errors
|
IMSL_NOT_CONVERGENT |
The maximum number of function evaluations has been reached, and convergence has not been attained |
|
IMSL_STOP_USER_FCN |
Request from user supplied function to stop algorithm. |