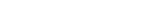int_fcn_trig
Integrates a function containing a sine or a cosine factor.
Synopsis
#include <imsl.h>
float imsl_f_int_fcn_trig (float fcn(), float a, float b, Imsl_quad weight, float omega, …, 0)
The type double function is imsl_d_int_fcn_trig.
Required Arguments
float fcn (float x) (Input)
User-supplied function to be integrated.
float a (Input)
Lower limit of integration.
float b (Input)
Upper limit of integration.
Imsl_quad weight and float omega (Input)
These two parameters are used to describe the trigonometric weight. The parameter weight can take on the two values described below, and the parameter omega = ω specifies the frequency of the trigonometric weighting function.
|
weight |
Integration Weight |
|
IMSL_COS |
cos (ωx) |
|
IMSL_SIN |
sin (ωx) |
Return Value
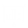
The value of
is returned if weight = IMSL_COS. If weight = IMSL_SIN, then the cosine factor is replaced with a sine factor. If no value can be computed, NaN is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float imsl_f_int_fcn_trig (float fcn(), float a, float b, Imsl_quad weight, float omega,
IMSL_ERR_ABS, float err_abs,
IMSL_ERR_REL, float err_rel,
IMSL_ERR_EST, float *err_est,
IMSL_MAX_SUBINTER, int max_subinter,
IMSL_N_SUBINTER, int *n_subinter,
IMSL_N_EVALS, int *n_evals,
IMSL_MAX_MOMENTS, int max_moments,
IMSL_FCN_W_DATA, float fcn(), void *data,
0)
Optional Arguments
IMSL_ERR_ABS, float err_abs (Input)
Absolute accuracy desired.
Default: where ɛ is the machine precision
IMSL_ERR_REL, float err_rel (Input)
Relative accuracy desired.
Default: where ɛ is the machine precision
IMSL_ERR_EST, float *err_est (Output)
Address to store an estimate of the absolute value of the error.
IMSL_MAX_SUBINTER, int max_subinter (Input)
Number of subintervals allowed.
Default: max_subinter = 500
IMSL_N_SUBINTER, int *n_subinter (Output)
Address to store the number of subintervals generated.
IMSL_N_EVALS, int *n_evals (Output)
Address to store the number of evaluations of fcn.
IMSL_MAX_MOMENTS, int max_moments (Input)
This is an upper bound on the number of Chebyshev moments that can be stored. Increasing (decreasing) this number may increase (decrease) execution speed and space used.
Default: max_moments = 21
IMSL_FCN_W_DATA, float fcn (float x, void *data), void *data (Input)
User supplied function to be integrated, which also accepts a pointer to data that is supplied by the user. data is a pointer to the data to be passed to the user-supplied function. See Passing Data to User-Supplied Functions in the introduction to this manual for more details.
Description
The function imsl_f_int_fcn_trig is a special-purpose integrator that uses a globally adaptive scheme to reduce the absolute error. It computes integrals whose integrands have the special form w(x)f(x) where w(x) is either cos(ωx) or sin(ωx). Depending on the length of the subinterval in relation to the size of ω, either a modified Clenshaw-Curtis procedure or a Gauss-Kronrod 7∕15 rule is employed to approximate the integral on a subinterval. This function uses the general strategy of the function imsl_f_int_fcn_sing.
On some platforms,imsl_f_int_fcn_trig can evaluate the user-supplied function fcn in parallel. This is done only if the function imsl_omp_options is called to flag user-defined functions as thread-safe. A function is thread-safe if there are no dependencies between calls. Such dependencies are usually the result of writing to global or static variables.
The function imsl_f_int_fcn_trig is based on the subroutine QAWO by Piessens et al. (1983).
Examples
Example 1
The value of
is computed. Notice that we have coded around the singularity at zero. This is necessary since this procedure evaluates the integrand at the two endpoints.
#include <imsl.h>
#include <stdio.h>
#include <math.h>
float fcn(float x);
int main()
{
float q, exact, omega;
omega = 10*imsl_f_constant("pi",
0);
imsl_omp_options(
IMSL_SET_FUNCTIONS_THREAD_SAFE, 1,
0);
/* Evaluate the integral */
q = imsl_f_int_fcn_trig (fcn, 0.0, 1.0,
IMSL_SIN, omega,
0);
/* Print the result and the */
/* exact answer */
exact = -.1281316;
printf("integral = %10.3f\nexact = %10.3f\n", q, exact);
}
float fcn(float x)
{
return (x==0.0) ? 0.0 : log(x);
}
Output
integral = -0.128
exact = -0.128
The value of
is again computed. The values of the actual and estimated error are printed as well. Note that these numbers are machine dependent. Furthermore, it is usually the case that the error estimate is pessimistic. That is, the actual error is usually smaller than the error estimate as is the case in this example. The number of function evaluations are also printed.
#include <imsl.h>
#include <stdio.h>
#include <math.h>
float fcn(float x);
int main()
{
int n_evals;
float q, exact, omega, err_est, exact_err;
omega = 10*imsl_f_constant("pi",
0);
imsl_omp_options(
IMSL_SET_FUNCTIONS_THREAD_SAFE, 1,
0);
/* Evaluate the integral */
q = imsl_f_int_fcn_trig (fcn, 0.0, 1.0,
IMSL_SIN, omega,
IMSL_ERR_EST, &err_est,
IMSL_N_EVALS, &n_evals,
0);
/* Print the result and the */
/* exact answer */
exact = -.1281316;
exact_err = fabs(exact - q);
printf("integral = %10.3f\nexact = %10.3f\n", q, exact);
printf("error estimate = %e\nexact error = %e\n", err_est,
exact_err);
printf("The number of function evaluations = %d\n", n_evals);
}
float fcn(float x)
{
return (x==0.0) ? 0.0 : log(x);
}
Output
integral = -0.128
exact = -0.128
error estimate = 7.504603e-05
exact error = 5.245209e-06
The number of function evaluations = 215
Warning Errors
|
IMSL_ROUNDOFF_CONTAMINATION |
Roundoff error, preventing the requested tolerance from being achieved, has been detected. |
|
IMSL_PRECISION_DEGRADATION |
A degradation in precision has been detected. |
|
IMSL_EXTRAPOLATION_ROUNDOFF |
Roundoff error in the extrapolation table, preventing the requested tolerance from being achieved, has been detected. |
Fatal Errors
|
IMSL_DIVERGENT |
Integral is probably divergent or slowly convergent. |
|
IMSL_MAX_SUBINTERVALS |
The maximum number of subintervals allowed has been reached. |
|
IMSL_STOP_USER_FCN |
Request from user supplied function to stop algorithm. User flag = "#". |