poisson_cdf

Evaluates the Poisson distribution function.

Synopsis

#include <imsl.h>

float imsl_f_poisson_cdf (int k, float theta)

The type double function is imsl_d_poisson_cdf.

Required Arguments

int k (Input)
Argument for which the Poisson distribution function is to be evaluated.

float theta (Input)
Mean of the Poisson distribution. Argument theta must be positive.

Return Value

The probability that a Poisson random variable takes a value less than or equal to k.

Description

The function imsl_f_poisson_cdf evaluates the distribution function of a Poisson random variable with parameter theta. The mean of the Poisson random variable, theta, must be positive. The probability function (with θ = theta) is

f(x) = e-q θx/x!, for x = 0, 1, 2, …

The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed. The function imsl_f_poisson_cdf uses the recursive relationship

f(x + 1) = f(x)q/(x + 1), for x = 0, 1, 2, …, k - 1

with f(0) = e-q.

 

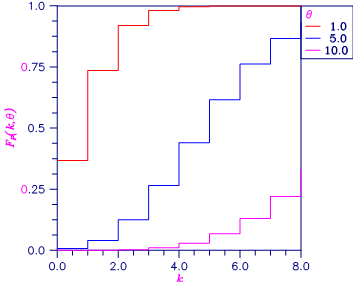
Figure 1,  Plot of Fp(k, θ)

Example

Suppose X is a Poisson random variable with θ = 10. This example evaluates the probability that X ≤ 7.

 

#include <imsl.h>

 

int main()

{

int k = 7;

float theta = 10.0;

float p;

 

p = imsl_f_poisson_cdf(k, theta);

printf("Pr(x <= 7) = %6.4f\n", p);

}

Output

 

Pr(x <= 7) = 0.2202

Informational Errors

IMSL_LESS_THAN_ZERO

The input argument, k, is less than zero.