Evaluates the real modified Bessel function of the second kind of order zero K0(x).
Synopsis
#include <imsl.h>
float imsl_f_bessel_K0 (float x)
The type double procedure is imsl_d_bessel_K0.
Required Arguments
float x
(Input)
Point at which the modified Bessel function is to be evaluated. It
must be positive.
Return Value
The value of the modified Bessel function
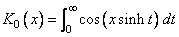
If no solution can be computed, then NaN is returned.
Description
Since K0(x) is complex for negative x and is undefined at x = 0, imsl_f_bessel_K0 is defined only for x > 0. For large x, imsl_f_bessel_K0 will underflow.
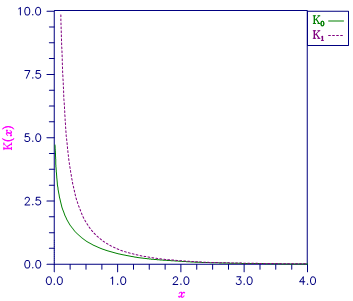
Figure 9- 12 Plot of K0(x) and K1(x)
Example
The Bessel function K0(1.5) is evaluated.
#include
<imsl.h>
main()
{
float x = 1.5;
float ans;
ans =
imsl_f_bessel_K0(x);
printf("K0(%f) = %f\n", x,
ans);
}
Output
K0(1.500000) = 0.213806
Alert Errors
IMSL_LARGE_ARG_UNDERFLOW The argument x must not be so large that the result (approximately equal to

underflows.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |