Evaluates the real Bessel function of the second kind of order one Y1(x).
Synopsis
#include <imsl.h>
float imsl_f_bessel_Y1 (float x)
The type double procedure is imsl_d_bessel_Y1.
Required Arguments
float x
(Input)
Point at which the Bessel function is to be evaluated.
Return Value
The value of the Bessel function
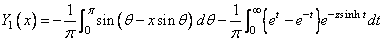
If no solution can be computed, then NaN is returned.
Description
This function is sometimes called the Neumann function, N1(x), or Weber’s function.
Since Y1(x) is complex for negative x and is undefined at x = 0, imsl_f_bessel_Y1 is defined only for x > 0. Because the Bessel function Y1(x) is oscillatory, its computation becomes inaccurate as x increases.
Example
The Bessel function Y1(1.5) is evaluated.
#include
<imsl.h>
main()
{
float x = 1.5;
float ans;
ans =
imsl_f_bessel_Y1(x);
printf("Y1(%f) = %f\n", x,
ans);
}
Output
Y1(1.500000) = -0.412309
Warning Errors
IMSL_LARGE_ABS_ARG_WARN
|x| should be less tha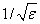n 
where ɛ
is the machine precision to prevent the answer from being less accurate than
half precision.
Fatal Errors
IMSL_SMALL_ARG_OVERFLOW The argument x must be large enough (x > max (1/b, s) where s is the smallest repesentable positive number and b is the largest repesentable number) that Y1(x) does not overflow.
IMSL_LARGE_ABS_ARG_FATAL |x| should be less than 1/ɛ where ɛ is the machine precision for the answer to have any precision.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |