.p>.CMCH6.DOC!CONVOLUTION;convolution
Computes the convolution, and optionally, the correlation of two real vectors.
Synopsis
#include <imsl.h>
float *imsl_f_convolution (int nx, float x[], int ny, float y[], int *nz, ¼, 0)
The type double function is imsl_d_convolution.
Required Arguments
int nx
(Input)
Length of the vector x.
float x[]
(Input)
Real vector of length nx.
int ny
(Input)
Length of the vector y.
float y[]
(Input)
Real vector of length ny.
int *nz
(Output)
Length of the output vector.
Return Value
A pointer to an array of length nz containing the convolution of x and y. To release this space, use free. If no zeros are computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_convolution (int
nx,
float
x[],
int
ny,
float
y[],
int *nz,
IMSL_PERIODIC,
IMSL_CORRELATION,
IMSL_FIRST_CALL,
IMSL_CONTINUE_CALL,
IMSL_LAST_CALL,
IMSL_RETURN_USER, float
z[],
IMSL_Z_TRANS, float
**zhat
IMSL_Z_TRANS_USER, float
*zhat,
0)
Optional Arguments
IMSL_PERIODIC
The
input is periodic.
IMSL_CORRELATION
Return
the correlation of x and y.
IMSL_FIRST_CALL
If
the function is called multiple times with the same nx and ny, select this option
on the first call.
IMSL_CONTINUE_CALL
If
the function is called multiple times with the same nx and ny, select this option
on intermediate calls.
IMSL_LAST_CALL
If
the function is called multiple times with the same nx and ny, select this option
on the final call.
IMSL_RETURN_USER, float z[]
(Output)
User-supplied array of length at least nz containing the
convolution or correlation of x and y.
IMSL_Z_TRANS, float **zhat[]
(Output)
Address of a pointer to an array of length at least nz containing on
output the discrete Fourier transform of z.
IMSL_Z_TRANS_USER, float zhat[]
(Output)
User-supplied array of length at least nz containing on
output the discrete Fourier transform of z.
Description
The function imsl_f_convolution, by default, computes the discrete convolution of two sequences x and y. More precisely, let nx be the length of x, and ny denote the length of y. If a circular convolution is desired, the optional argument IMSL_PERIODIC must be selected. We set
nz = max {ny, nx},
and we pad out the shorter vector with zeros. Then, we compute
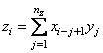
where the index on x is interpreted as a positive number between 1 and nz, modulo nz.
The technique used to compute the zi’s is based on the fact that the (complex discrete) Fourier transform maps convolution into multiplication. Thus, the Fourier transform of z is given by
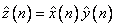
where the following equation is true.
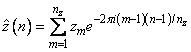
The technique used here to compute the convolution is to take the discrete Fourier transform of x and y, multiply the results together component-wise, and then take the inverse transform of this product. It is very important to make sure that nz is the product of small primes if option IMSL_PERIODIC is selected. If nz is a product of small primes, then the computational effort will be proportional to nzlog(nz). If option IMSL_PERIODIC is not selected, then a good value is chosen for nz so that the Fourier transforms are efficient and nz ³ nx + ny − 1. This will mean that both vectors will be padded with zeros.
We point out that no complex transforms of x or y are taken since both sequences are real, and real transforms can simulate the complex transform above. Such a strategy is six times faster and requires less space than when using the complex transform.
Optionally, the function imsl_f_convolution computes the discrete correlation of two sequences x and y. More precisely, let n be the length of x and y. If a circular correlation is desired, then option IMSL_PERIODIC must be selected. We set (on output)
nz = n if IMSL_PERIODIC is chosen
(nz = 2a3b5g ³ 2n − 1) if IMSL_PERIODIC is not chosen
where α, β, and γ are nonnegtive integers yielding the smallest number of the type 2a3b5g satisfying the inequality. Once nz is determined, we pad out the vectors with zeros. Then, we compute
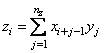
where the index on x is interpreted as a positive number between one and nz, modulo nz. Note that this means that
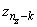
contains the correlation of x(k − 1) with y as
k = 0, 1, ¼,
nz∕2. Thus, if
x(k − 1) = y(k)
for all k, then we would expect
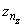
to be the largest component of z. The technique used to compute the zi’s is based on the fact that the (complex discrete) Fourier transform maps correlation into multiplication. Thus, the Fourier transform of z is given by
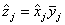
where the following equation is true.
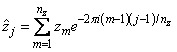
Thus, the technique used here to compute the correlation is to take the discrete Fourier transform of x and the conjugate of the discrete Fourier transform of y, multiply the results together component-wise, and then take the inverse transform of this product. It is very important to make sure that nz is the product of small primes if IMSL_PERIODIC is selected. If nz is the product of small primes, then the computational effort will be proportional to nzlog (nz). If IMSL_PERIODIC is not chosen, then a good value is chosen for nz so that the Fourier transforms are efficient and nz ³ 2n − 1. This will mean that both vectors will be padded with zeros.
We point out that no complex transforms of x or y are taken since both sequences are real, and real transforms can simulate the complex transform above. Such a strategy is six times faster and requires less space than when using the complex transform.
Examples
Example 1
This example computes a nonperiodic convolution. The idea here is that you can compute a moving average of the type found in digital filtering using this function. The averaging operator in this case is especially simple and is given by averaging five consecutive points in the sequence. We try to recover the values of an exponential function contaminated by noise. The large error for the last value has to do with the fact that the convolution is averaging the zeros in the “pad” rather than the function values. Notice that the signal size is 100, but only reports the errors at 10 points.
#include "imsl.h"
#include
<math.h>
#define NFLTR 5
#define
NY 100
/* Define function */
#define F1(A)
exp(A)
main()
{
int i, k,
nz;
float fltr[NFLTR],
fltrer, origer, total1, total2, twopi,
x, y[NY], *z, *noise;
/* Set
up the filter */
for (i = 0; i < NFLTR; i++) fltr[i] =
0.2;
/*
* Set up y-vector for the
nonperiodic casE.
*/
twopi = 2.0*imsl_f_constant ("Pi",
0);
imsl_random_seed_set(1234579);
noise = imsl_f_random_uniform(NY, 0);
for (i = 0; i
< NY; i++) {
x = (float)(i) /
(NY - 1);
y[i] = F1(x) + 0.5
*noise[i] - 0.25;
}
/*
* Call the convolution
routine for the nonperiodic
case.
*/
z = imsl_f_convolution(NFLTR, fltr, NY, y, &nz,
0);
/*
* Call test routines to
check z & zhat here. Print
results
*/
printf("\n Nonperiodic Case\n");
printf("
x
F1(x) Original
Error");
printf(" Filtered Error\n");
total1 = 0.0;
total2 =
0.0;
for (i = 0; i < NY; i++) {
if (i >=
NY-2)
k =
i - NY + 2;
else
k = i
+ 2;
x = (float)(i) / (float) (NY
- 1);
origer = fabs(y[i] -
F1(x));
fltrer = fabs(z[i+2] -
F1(x));
if ((i % 11) == 0)
{
printf("
%10.4f%13.4f%18.4f%18.4f\n",
x, F1(x), origer, fltrer);
}
total1 +=
origer;
total2 +=
fltrer;
}
printf(" Average absolute
error before
filter:%10.5f\n",
total1 / (NY));
printf(" Average absolute error
after
filter:%11.5f\n",
total2 / (NY));
}
Output
Nonperiodic
Case
x
F1(x) Original Error
Filtered Error
0.0000
1.0000
0.0811
0.3523
0.1111
1.1175
0.0226
0.0754
0.2222
1.2488
0.1526
0.0488
0.3333
1.3956
0.0959
0.0161
0.4444
1.5596
0.1747
0.0276
0.5556
1.7429
0.1035
0.0250
0.6667
1.9477
0.0402
0.0562
0.7778
2.1766
0.0673
0.0835
0.8889
2.4324
0.1044
0.0050
1.0000
2.7183
0.0154
1.1255
Average absolute error before filter: 0.12481
Average
absolute error after filter: 0.06785
Example 2
This example computes both a periodic correlation between two distinct signals x and y. There are 100 equally spaced points on the interval [0, 2π] and f1(x) = sin (x). Define x and y as follows:
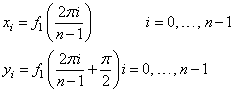
Note that the maximum value of z (the correlation of x with) occurs at i = 25, which corresponds to the offset.
#include "imsl.h"
#include
<math.h>
#define N
100
/* Define function
*/
#define F1(A)
sin(A)
main()
{
int i, k,
nz;
float pi,
max,
x[N], y[N], *z, xnorm, ynorm;
/*
* Set up y-vector for the
nonperiodic case.
*/
pi = imsl_f_constant ("Pi",
0);
for (i = 0; i < N; i++)
{
x[i] = F1(2.0*pi*(float)(i) /
(N-1));
y[i] =
F1(2.0*pi*(float)(i) / (N-1) + pi/2.0);
}
/*
* Call the correlation
function for the nonperiodic
case.
*/
z = imsl_f_convolution(N, x, N, y, &nz,
IMSL_CORRELATION, IMSL_PERIODIC,0);
xnorm =
imsl_f_vector_norm (N, x, 0);
ynorm = imsl_f_vector_norm
(N, y, 0);
for (i = 0; i < N; i++)
{
z[i] /=
xnorm*ynorm;
}
max =
z[0];
k = 0;
for (i = 1; i < N;
i++) {
if (max < z[i])
{
max =
z[i];
k =
i;
}
}
printf("The element of Z with the largest
normalized\n");
printf("value is Z(%2d).\n",
k);
printf("The normalized value of Z(%2d) is %6.3f\n", k,
z[k]);
}
Output
The element of Z with the largest normalized
value is
Z(25).
The normalized value of Z(25) is 1.000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |