Integrate a function on a hyper-rectangle,

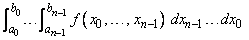
Synopsis

#include <imsl.h>

float imsl_f_int_fcn_hyper_rect (float fcn(), int ndim, float a[],
float b[], ¼, 0)

The type double function is imsl_d_int_fcn_hyper_rect.

Required Arguments

float fcn (int ndim, float x[])   (Input)
User-supplied function to be integrated.

int ndim   (Input)
The dimension of the hyper-rectangle.

float a[]   (Input)
Lower limits of integration.

float b[]   (Input)
Upper limits of integration.

Return Value

The value of

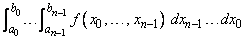
is returned. If no value can be computed, then NaN is returned.

Synopsis with Optional Arguments

#include <imsl.h>

float imsl_f_int_fcn_hyper_rect (float fcn(), int ndim, float a[], float b[], IMSL_ERR_ABS, float err_abs,
IMSL_ERR_REL, float err_rel,
IMSL_ERR_EST, float *err_est,
IMSL_MAX_EVALS, int max_evals,
IMSL_FCN_W_DATA, float fcn(), void *data,
0)

Optional Arguments

IMSL_ERR_ABS, float err_abs   (Input)
Absolute accuracy desired.
Default: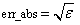

where ɛ is the machine precision

IMSL_ERR_REL, float err_rel   (Input)
Relative accuracy desired.
Default: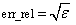

where ɛ is the machine precision

IMSL_ERR_EST, float *err_est   (Output)
Address to store an estimate of the absolute value of the error.

IMSL_MAX_EVALS, int max_evals   (Input)
Number of evaluations allowed.
Default: max_evals = 32n.

IMSL_FCN_W_DATA, float fcn (int ndim, float x[], void *data), void *data (Input)
User supplied function to be integrated, which also accepts a pointer to data that is supplied by the user.  data is a pointer to the data to be passed to the user-supplied function.  See the Introduction, Passing Data to User-Supplied Functions at the beginning of this manual for more details.

Description

The function imsl_f_int_fcn_hyper_rect approximates the n-dimensional iterated integral

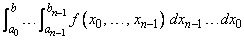
An estimate of the error is returned in the optional argument err_est. The approximation is achieved by iterated applications of product Gauss formulas. The integral is first estimated by a two-point tensor product formula in each direction. Then for i = 1, ¼, n, the function calculates a new estimate by doubling the number of points in the i-th direction, then halving the number immediately afterwards if the new estimate does not change appreciably. This process is repeated until either one complete sweep results in no increase in the number of sample points in any dimension; the number of Gauss points in one direction exceeds 256; or the number of function evaluations needed to complete a sweep exceeds max_evals.

Example

In this example, we compute the integral of

on an expanding cube. The values of the error estimates are machine dependent. The exact integral over R3 is π3/2.

#include <math.h>
#include <imsl.h>

float           fcn(int n, float x[]);
 
main()
{
    int         i, j, ndim = 3;
    float       q, limit, a[3], b[3];

    printf("       integral       limit \n");
    limit = pow(imsl_f_constant("pi",0), 1.5);
                                /* Evaluate the integral */
    for (i = 0;  i < 6;  i++) {
        for (j = 0; j < 3;  j++) {
            a[j] = -(i+1)/2.;
            b[j] = (i+1)/2.;
        }
        q = imsl_f_int_fcn_hyper_rect (fcn, ndim, a, b, 0);
                                /* Print the result and the */
                                /* limiting answer */
        printf("   %10.3f    %10.3f\n", q, limit);
    }
}

float fcn(int n, float x[])
{  
    float     s;
    s = x[0]*x[0] + x[1]*x[1] + x[2]*x[2];
    return  exp(-s);
}

 

 

Output

integral       limit
 0.785         5.568
 3.332         5.568
 5.021         5.568
 5.491         5.568
 5.561         5.568
 5.568         5.568

Warning Errors

IMSL_MAX_EVALS_TOO_LARGE                The argument max_evals was set greater than 28n.

Fatal Errors

IMSL_NOT_CONVERGENT                            The maximum number of function evaluations has been reached, and convergence has not been attained.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260