Solves a real symmetric nonnegative definite system of linear equations Ax = b. Using options, computes a Cholesky factorization of the matrix A, such that A = RTR = LLT. Computes the solution to Ax = b given the Cholesky factor.
Synopsis
#include <imsl.h>
float *imsl_f_lin_sol_nonnegdef (int n, float a[], float b[], …, 0)
The type double function is imsl_d_lin_sol_nonnegdef.
Required Arguments
int n
(Input)
Number of rows and columns in the matrix.
float a[]
(Input)
Array of size n × n containing the matrix.
float b[]
(Input)
Array of size n containing the right-hand side.
Return Value
Using required arguments, imsl_f_lin_sol_nonnegdef returns a pointer to a solution x of the linear system. To release this space, use free. If no value can be computed, NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_lin_sol_nonnegdef (int
n, float
a[],
float
b[],
IMSL_RETURN_USER, float
x[],
IMSL_A_COL_DIM, int
a_col_dim,
IMSL_FACTOR, float
**p_factor,
IMSL_FACTOR_USER, float
factor[],
IMSL_FAC_COL_DIM, int
fac_col_dim,
IMSL_INVERSE, float
**p_inva,
IMSL_INVERSE_USER, float
inva[],
IMSL_INV_COL_DIM, int
inv_col_dim,
IMSL_TOLERANCE, float
tol,
IMSL_FACTOR_ONLY,
IMSL_SOLVE_ONLY,
IMSL_INVERSE_ONLY,
0)
Optional Arguments
IMSL_RETURN_USER, float x[]
(Output)
A user-allocated array of length n containing the solution
x. When this option is specified, no storage is allocated for the
solution, and imsl_f_lin_sol_nonnegdef
returns a pointer to the array x.
IMSL_A_COL_DIM, int a_col_dim
(Input)
The column dimension of the array a.
Default: a_col_dim = n
IMSL_FACTOR, float
**p_factor (Output)
The address of a pointer to an array
of size n × n containing the LLT factorization
of A. When this option is specified, the space for the factor matrix is
allocated by imsl_f_lin_sol_nonnegdef.
The lower-triangular part of the factor array contains L, and the
upper-triangular part contains LTR. Typically, float *p_factor is declared,
and &p_factor is used
as an argument.
IMSL_FACTOR_USER, float factor[]
(Input/Output)
A user-allocated array of size n × n
containing the LLT factorization of A. The
lower-triangular part of factor contains
L, and the upper-triangular part contains LT. If a is not needed, a and factor can be the same
storage locations. If IMSL_SOLVE is
specified, this parameter is input; otherwise, it is output.
IMSL_FAC_COL_DIM, int
fac_col_dim (Input)
The column dimension of the array
containing the LLT factorization.
Default: fac_col_dim = n
IMSL_INVERSE, float **p_inva
(Output)
The address of a pointer to an array of size
n × n containing the inverse of A. The space for
this array is allocated by imsl_f_lin_sol_nonnegdef.
Typically, float *p_inva is declared,
and &p_inva
is used as an argument.
IMSL_INVERSE_USER, float inva[]
(Output)
A user-allocated array of size n × n
containing the inverse of A. If a is not needed, a and factor can be the same
storage locations. The storage locations for A cannot be the
factorization and the inverse of A at the same time.
IMSL_INV_COL_DIM, int
inva_col_dim (Input)
The column dimension of the array
containing the inverse of A.
Default: inva_col_dim = n
IMSL_TOLERANCE, float tol
(Input)
Tolerance used in determining linear dependence.
Default: tol = 100* imsl_f_machine(4)
See
the documentation for imsl_f_machine in
Chapter 12, “Utilities.”
IMSL_FACTOR_ONLY
Compute
the LLT factorization of A only. The
argument b is
ignored, and either the optional argument IMSL_FACTOR or IMSL_FACTOR_USER is
required.
IMSL_SOLVE_ONLY
Solve
Ax = b using the factorization previously computed by
this function. The argument a is ignored, and the
optional argument IMSL_FACTOR_USER is
required.
IMSL_INVERSE_ONLY
Compute
the inverse of A only. The argument b is ignored, and
either the optional argument IMSL_INVERSE or
IMSL_INVERSE_USER is
required.
Description
The function imsl_f_lin_sol_nonnegdef solves a system of linear algebraic equations having a symmetric nonnegative definite (positive semidefinite) coefficient matrix. It first computes a Cholesky (LLT or RTR) factorization of the coefficient matrix A.
The factorization algorithm is based on the work of Healy (1968) and proceeds sequentially by columns. The i-th column is declared to be linearly dependent on the first i − 1 columns if
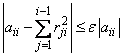
where ɛ (specified in tol) may be set by the user. When a linear dependence is declared, all elements in the i-th row of R (column of L) are set to zero.
Modifications due to Farebrother and Berry (1974) and Barrett and Healy (1978) for checking for matrices that are not nonnegative definite also are incorporated. The function imsl_f_lin_sol_nonnegdef declares A to not be nonnegative definite and issues an error message if either of the following conditions are satisfied:

Healy’s (1968) algorithm and the function imsl_f_lin_sol_nonnegdef permit the matrices A and R to occupy the same storage. Barrett and Healy (1978) in their remark neglect this fact. The function imsl_f_lin_sol_nonnegdef uses
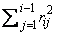
for aii in the above condition 2 to remedy this problem.
If an inverse of the matrix A is required and the matrix is not (numerically) positive definite, then the resulting inverse is a symmetric g2 inverse of A. For a matrix G to be a g2 inverse of a matrix A, G must satisfy conditions 1 and 2 for the Moore-Penrose inverse, but generally fail conditions 3 and 4. The four conditions for G to be a Moore-Penrose inverse of A are as follows:
1. AGA = A
2. GAG = G
3. AG is symmetric
4. GA is symmetric
The solution of the linear system Ax = b is computed by solving the factored version of the linear system RTRx = b as two successive triangular linear systems. In solving the triangular linear systems, if the elements of a row of R are all zero, the corresponding element of the solution vector is set to zero. For a detailed description of the algorithm, see Section 2 in Sallas and Lionti (1988).
Examples
Example 1
A solution to a system of four
linear equations is obtained. Maindonald (1984, pp. 83−86
and 104−105) discusses the
computations for the factorization and solution to this problem.
#include
<imsl.h>
main()
{
int n = 4;
float *x;
float a[] = {36.0, 12.0, 30.0, 6.0,
12.0, 20.0, 2.0, 10.0,
30.0, 2.0, 29.0, 1.0,
6.0, 10.0, 1.0, 14.0};
float b[] = {18.0, 22.0, 7.0,
20.0};
/* Solve Ax = b for x */
x =
imsl_f_lin_sol_nonnegdef(n, a, b,
0);
/* Print solution, x, of Ax = b */
imsl_f_write_matrix("Solution, x", 1, n, x, 0);
}
Output
Solution, x
1
2
3
4
0.167
0.500
0.000 1.000
Example 2
The symmetric nonnegative definite matrix in the initial example is used to compute the factorization only in the first call to lin_sol_nonnegdef. The space needed for the factor is provided by the user. On the second call, both the LLT factorization and the right-hand side vector in the first example are used as the input to compute a solution x. It also illustrates another way to obtain the solution array x.
#include
<imsl.h>
main()
{
int n = 4, a_col_dim =
6;
float factor[36],
x[5];
float a[] =
{36.0, 12.0, 30.0, 6.0,
12.0, 20.0, 2.0, 10.0,
30.0, 2.0, 29.0, 1.0,
6.0, 10.0, 1.0, 14.0};
float b[] = {18.0, 22.0, 7.0,
20.0};
/* Factor A */
imsl_f_lin_sol_nonnegdef(n, a,
b,
IMSL_FACTOR_USER,
factor,
IMSL_FAC_COL_DIM,
a_col_dim,
IMSL_FACTOR_ONLY,
0);
/* NULL is returned in
*/
/* this case. Another
*/
/* way to obtain the
*/
/* factor is to use the
*/
/* IMSL_FACTOR option. */
imsl_f_write_matrix("factor", n, n, factor,
IMSL_A_COL_DIM,
a_col_dim,
0);
/* Get the solution using
*/
/* the factorized matrix. */
imsl_f_lin_sol_nonnegdef(n,
a,
b,
IMSL_FACTOR_USER,
factor,
IMSL_FAC_COL_DIM,
a_col_dim,
IMSL_RETURN_USER,
x,
IMSL_SOLVE_ONLY,
0);
imsl_f_write_matrix("Solution, x, of Ax = b", 1, n, x,
0);
}
Output
factor
1
2
3 4
1
6
2
5
1
2
2
4
-2
2
3
5
-2
0
0
4
1
2
0
3
Solution, x, of Ax = b
1
2
3
4
0.167
0.500
0.000 1.000
Example 3
This example uses the IMSL_INVERSE option to compute the symmetric g inverse of the symmetric nonnegative matrix in the first example. Maindonald (1984, p. 106) discusses the computations for this problem.
#include <stdio.h>
#include
<imsl.h>
void main()
{
int n = 4;
float *p_a_inva, *p_a_inva_a,
*p_inva;
float a[] =
{36.0, 12.0, 30.0,
6.0,
12.0, 20.0, 2.0, 10.0,
30.0,
2.0, 29.0,
1.0,
6.0, 10.0, 1.0,
14.0};
/* Get g2_inverse(a) */
imsl_f_lin_sol_nonnegdef(n, a,
NULL,
IMSL_INVERSE,
&p_inva,
IMSL_INVERSE_ONLY,
0);
/* Form a*g2_inverse(a) */
p_a_inva =
imsl_f_mat_mul_rect("A*B",
IMSL_A_MATRIX, n, n,
a,
IMSL_B_MATRIX, n, n,
p_inva,
0);
/* Form a*g2_inverse(a)*a */
p_a_inva_a =
imsl_f_mat_mul_rect("A*B",
IMSL_A_MATRIX, n, n,
p_a_inva,
IMSL_B_MATRIX,
n, n,
a,
0);
imsl_f_write_matrix("The g2 inverse of a", n, n,
p_inva, 0);
imsl_f_write_matrix("a*g2_inverse(a)\nviolates
condition 3
of"
" the M-P inverse", n, n, p_a_inva, 0);
imsl_f_write_matrix("a = a*g2_inverse(a)*a\ncondition 1
of"
" the M-P inverse", n, n, p_a_inva_a, 0);
}
Output
The g2 inverse of
a
1
2
3
4
1 0.0347
-0.0208 0.0000
0.0000
2 -0.0208
0.0903 0.0000
-0.0556
3 0.0000
0.0000 0.0000
0.0000
4 0.0000
-0.0556 0.0000
0.1111
a*g2_inverse(a)
violates condition 3 of the M-P
inverse
1
2
3
4
1
1.0
-0.0
0.0
0.0
2
0.0
1.0
0.0
0.0
3
1.0
-0.5
0.0
0.0
4
0.0
-0.0
0.0
1.0
a = a*g2_inverse(a)*a
condition 1 of the M-P
inverse
1
2
3
4
1
36
12
30
6
2
12
20
2
10
3
30
2
29
1
4
6
10
1 14
Warning Errors
IMSL_INCONSISTENT_EQUATIONS_2 The linear system of equations is inconsistent.
IMSL_NOT_NONNEG_DEFINITE The matrix A is not nonnegative definite
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |