Solves a real symmetric positive definite system of linear equations Ax = b in band symmetric storage mode. Using optional arguments, any of several related computations can be performed. These extra tasks include computing the RTR Cholesky factorization of A, computing the solution of Ax = b given the Cholesky factorization of A, or estimating the L1 condition number of A.
Synopsis
#include <imsl.h>
float *imsl_f_lin_sol_posdef_band (int n, float a[], int ncoda, float b[], …, 0)
The type double procedure is imsl_d_lin_sol_posdef_band.
Required Arguments
int n
(Input)
Number of rows and columns in the matrix.
float a[]
(Input)
Array of size (ncoda + 1) × n containing the n ×
n positive definite band coefficient matrix in band symmetric storage
mode.
int ncoda
(Input)
Number of upper codiagonals of the matrix.
float b[]
(Input)
Array of size n containing the
right-hand side.
Return Value
A pointer to the solution x of the linear system Ax = b. To release this space use free. If no solution was computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float
*imsl_f_lin_sol_posdef_band (int n, float a[], int ncoda,
float b[],
IMSL_RETURN_USER, float x[],
IMSL_FACTOR,
float **p_factor,
IMSL_FACTOR_USER, float
factor[],
IMSL_CONDITION, float
*cond,
IMSL_FACTOR_ONLY,
IMSL_SOLVE_ONLY,
0)
Optional Arguments
IMSL_RETURN_USER, float x[]
(Output)
A user-allocated array of length n containing the solution
x.
IMSL_FACTOR, float
**p_factor (Output)
The address of a pointer to an array
of size (ncoda + 1) × n containing the
LLT factorization
of A. On return, the necessary space is allocated by imsl_f_lin_sol_posdef_band.
Typically, float *p_factor is declared
and &p_factor is used
as an argument.
IMSL_FACTOR_USER, float factor[]
(Input/Output)
A user-allocated array of size (ncoda + 1) × n
containing the LLT factorization of A in band
symmetric form. If A is not needed, factor and a can share the same
storage.
These parameters are “Input” if IMSL_SOLVE is specified. They are “Output” otherwise.
IMSL_CONDITION, float *cond
(Output)
A pointer to a scalar containing an estimate of the L1 norm condition
number of the matrix A. This option cannot be used with the option IMSL_SOLVE_ONLY.
IMSL_FACTOR_ONLY
Compute the LLT factorization
of A. If IMSL_FACTOR_ONLY is
used, either IMSL_FACTOR or IMSL_FACTOR_USER is
required. The argument b is then ignored, and
the returned value of imsl_f_lin_sol_posdef_band
is NULL.
IMSL_SOLVE_ONLY
Solve Ax = b given the
LLT
factorization previously computed by imsl_f_lin_sol_posdef_band.
By default, the solution to Ax = b is pointed to by imsl_f_lin_sol_posdef_band.
If IMSL_SOLVE_ONLY is
used, argument IMSL_FACTOR_USER is
required and the argument a is ignored.
Description
The function imsl_f_lin_sol_posdef_band solves a system of linear algebraic equations with a real symmetric positive definite band coefficient matrix A. It computes the RTR Cholesky factorization of A. R is an upper triangular band matrix.
When the solution to the linear system or the inverse of the matrix is sought, an estimate of the L1 condition number of A is computed using Higham’s modifications to Hager’s method, as given in Higham (1988). If the estimated condition number is greater than 1/ɛ (where ɛ is the machine precision), a warning message is issued. This indicates that very small changes in A may produce large changes in the solution x.
The function imsl_f_lin_sol_posdef_band fails if any submatrix of R is not positive definite or if R has a zero diagonal element. These errors occur only if A is very close to a singular matrix or to a matrix which is not positive definite.
The function imsl_f_lin_sol_posdef_band is partially based on the LINPACK subroutines CPBFA and SPBSL; see Dongarra et al. (1979).
Example 1
Solves a system of linear equations Ax = b, where
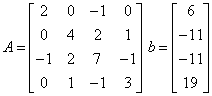
#include <imsl.h>
void main()
{
int n = 4;
int ncoda = 2;
float *x;
/* Note that a is in band storage mode */
float a[] = {0.0, 0.0, -1.0, 1.0,
0.0, 0.0, 2.0, -1.0,
2.0, 4.0, 7.0, 3.0};
float b[] = {6.0, -11.0, -11.0, 19.0};
x =
imsl_f_lin_sol_posdef_band (n, a, ncoda, b, 0);
imsl_f_write_matrix ("Solution, x, of Ax = b", 1, n, x, 0);
}
Output
Solution, x, of Ax = b
1 2 3 4
4 -6 2 9
Example 2
This example solves the same problem Ax = b given in the first example. The solution is returned in user-allocated space and an estimate of κ1(A) is computed. Additionally, the RTR factorization is returned. Then, knowing that κ1(A) = ||A|| ||A-1||, the condition number is computed directly and compared to the estimate from Higham’s method.
#include <imsl.h>
void
main()
{
int n = 4;
int ncoda = 2;
float a[] = {0.0, 0.0, -1.0, 1.0,
0.0, 0.0, 2.0, -1.0,
2.0, 4.0, 7.0, 3.0};
float b[] = {6.0, -11.0, -11.0, 19.0};
float x[4];
float e_i[4];
float *factor;
float condition;
float column_norm;
float inverse_norm;
int i;
int j;
imsl_f_lin_sol_posdef_band (n, a, ncoda, b,
IMSL_FACTOR, &factor,
IMSL_CONDITION, &condition,
IMSL_RETURN_USER, x,
0);
imsl_f_write_matrix ("Solution, x, of Ax = b", 1, n, x, 0);
/* find one norm of inverse */
inverse_norm =
0.0;
for (i=0; i<n; i++) {
for (j=0; j<n; j++) e_i[j] = 0.0;
e_i[i] = 1.0;
/* determine one norm of each column of inverse */
imsl_f_lin_sol_posdef_band (n, a, ncoda, e_i,
IMSL_FACTOR_USER, factor,
IMSL_SOLVE_ONLY,
IMSL_RETURN_USER, x,
0);
column_norm = imsl_f_vector_norm (n, x,
IMSL_ONE_NORM,
0);
/* the max of the column norms is the norm of
inv(A) */
if (inverse_norm < column_norm)
inverse_norm = column_norm;
}
/* by observation, one norm of A is 11 */
printf
("\nHigham’s condition estimate = %f\n", condition);
printf ("Direct condition estimate = %f\n",
11.0*inverse_norm);
}
Output
Solution, x, of Ax = b
1 2 3 4
4 -6 2 9
Higham’s condition estimate = 8.650485
Direct condition estimate = 8.650485
Warning Errors
IMSL_ILL_CONDITIONED
The input matrix is too ill-conditioned. An estimate of the reciprocal of
its L1 condition number is
"rcond" = #. The
solution might not be accurate.
Fatal Errors
IMSL_NONPOSITIVE_MATRIX The leading # by # submatrix of the input matrix is not positive definite.
IMSL_SINGULAR_MATRIX The input matrix is singular.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |