.p>.CMCH3.DOC!SPLINE_2D_INTEGRAL;spline_2d_integral
Evaluates the integral of a tensor-product spline on a rectangular domain.
Synopsis
#include <imsl.h>
float imsl_f_spline_2d_integral (float a, float b, float c, float d, Imsl_f_spline *sp)
The type double function is imsl_d_spline_2d_integral.
Required Arguments
float a (Input)
float b
(Input)
The integration limits for the first variable of the tensor-product
spline.
float c (Input)
float d
(Input)
The integration limits for the second variable of the tensor-product
spline.
Imsl_f_spline *sp
(Input)
Pointer to the structure that represents the spline.
Return Value
The value of the integral of the
tensor-product spline over the rectangle
[a, b] ´ [c, d]. If no value can be
computed, NaN is returned.
Description
The function imsl_f_spline_2d_integral computes the integral of a tensor-product spline. If s is the spline, then this function returns
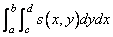
This function uses the (univariate integration) identity (22) in de Boor (1978, p. 151)
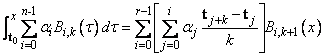
where t0 ≤ x ≤ tr.
It assumes (for all knot sequences) that the first and last k knots are stacked, that is, t0 = … = tk-1 and tn = … = tn+k-1 , where k is the order of the spline in the x or y direction.
Example
This
example integrates a two-dimensional, tensor-product spline over the rectangle
[0, x] ´ [0,
y].
#include
<imsl.h>
#include <stdio.h>
#include
<math.h>
#define
NDATA 11
#define
OUTDATA
2
/* Define function */
#define
F(x,y)
(float)(x*x*x+y*y)
/* The integral of F from 0 to x
*/
/* and 0 to y */
#define
FI(x,y) (float)(y*x*x*x*x/4. +
x*y*y*y/3.)
main()
{
int
i, j, num_xdata, num_ydata;
float
fdata[NDATA][NDATA], xdata[NDATA], ydata[NDATA];
float
x, y, z;
Imsl_f_spline
*sp;
/* Set up grid */
for (i = 0; i <
NDATA; i++) {
xdata[i] =
ydata[i] = (float) i / ((float)(NDATA-1));
}
for (i = 0; i < NDATA; i++)
{
for (j = 0; j < NDATA;
j++) {
fdata[i][j] =
F(xdata[i],ydata[j]);
}
}
num_xdata = num_ydata =
NDATA;
/* Compute tensor-product interpolant */
sp =
imsl_f_spline_2d_interp(num_xdata, xdata,
num_ydata,
ydata, fdata,
0);
/* Print results */
printf("
x y
FI(x, y) Integral
Error\n");
for (i = 0; i < OUTDATA; i++)
{
x = (float) (1+i) / (float)
(OUTDATA+1);
for (j = 0; j
< OUTDATA; j++)
{
y =
(float) (1+j) / (float)
(OUTDATA+1);
z = imsl_f_spline_2d_integral(0.0, x, 0.0, y,
sp);
printf(" %6.3f %6.3f %10.3f %10.3f
%10.4f\n",
x, y, FI(x, y), z,
fabs(FI(x,y)-z));
}
}
}
Output
x
y FI(x, y)
Integral Error
0.333
0.333
0.005 0.005
0.0000
0.333
0.667
0.035
0.035 0.0000
0.667
0.333
0.025
0.025 0.0000
0.667
0.667
0.099
0.099 0.0000
Warning Errors
IMSL_SPLINE_LEFT_ENDPT The left endpoint of X integration is not within the knot sequence. Integration occurs only from torder-1 to b.
IMSL_SPLINE_RIGHT_ENDPT The right endpoint of X integration is not within the knot sequence. Integration occurs only from torder-1 to a.
IMSL_SPLINE_LEFT_ENDPT_1
The left endpoint of X integration is not within the knot sequence.
Integration occurs only from b to
tspline_space_dim-1.
IMSL_SPLINE_RIGHT_ENDPT_1 The right endpoint of X integration is not within the knot sequence. Integration occurs only from a to tspline_space_dim-1.
IMSL_SPLINE_LEFT_ENDPT_2 The left endpoint of Y integration is not within the knot sequence. Integration occurs only from torder-1 to d.
IMSL_SPLINE_RIGHT_ENDPT_2 The right endpoint of Y integration is not within the knot sequence. Integration occurs only from torder-1 to c.
IMSL_SPLINE_LEFT_ENDPT_3
The left endpoint of Y integration is not within the knot sequence.
Integration occurs only from d to
tspline_space_dim-1.
IMSL_SPLINE_RIGHT_ENDPT_3
The right endpoint of Y integration is not within the knot sequence.
Integration occurs only from c to
tspline_space_dim-1.
Fatal Errors
IMSL_KNOT_MULTIPLICITY Multiplicity of the knots cannot exceed the order of the spline.
IMSL_KNOT_NOT_INCREASING The knots must be nondecreasing.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |