Finds the zeros of a polynomial with real coefficients using the Jenkins-Traub, three-stage algorithm.

Synopsis

#include <imsl.h>

f_complex *imsl_f_zeros_poly (int ndeg, float coef[], ¼, 0)

The type d_complex function is imsl_d_zeros_poly.

Required Arguments

int ndeg   (Input)
Degree of the polynomial.

float coef[]   (Input)
Array with ndeg + 1 components containing the coefficients of the polynomial in increasing order by degree. The polynomial is
coef[n] zn + coef [n − 1] zn-1 + ¼ + coef [0], where n = ndeg.

Return Value

A pointer to the complex array of zeros of the polynomial. To release this space, use free. If no zeros are computed, then NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

f_complex *imsl_f_zeros_poly (int ndeg, float coef[],
IMSL_RETURN_USER, f_complex root[],
0)

Optional Arguments

IMSL_RETURN_USER, f_complex root[]   (Output)
Array with ndeg components containing the zeros of the polynomial.

Description

The function imsl_f_zeros_poly computes the n zeros of the polynomial

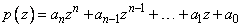
where the coefficients ai for i = 0, 1, ¼, n are real and n is the degree of the polynomial.

The function imsl_f_zeros_poly uses the Jenkins-Traub, three-stage algorithm (Jenkins and Traub 1970; Jenkins 1975). The zeros are computed one at a time for real zeros or two at a time for a complex conjugate pair. As the zeros are found, the real zero, or quadratic factor, is removed by polynomial deflation.

Examples

Example 1

This example finds the zeros of the third-degree polynomial

p(z) = z3 − 3z2 + 4z – 2

where z is a complex variable.

#include <imsl.h>

#define NDEG    3

main()
{
        f_complex       *zeros;
        static float    coeff[NDEG + 1] = {-2.0, 4.0, -3.0, 1.0};

        zeros = imsl_f_zeros_poly(NDEG, coeff, 0);

        imsl_c_write_matrix ("The complex zeros found are", 1, 3,
            zeros, 0);
}

 

Output

                       The complex zeros found are
                      1                        2                        3
(         1,         0)  (         1,         1)  (         1,        -1)

 

Example 2

The same problem is solved with the return option.

#include <imsl.h>

#define NDEG    3

main()
{
        f_complex       zeros[3];
        static float    coeff[NDEG + 1] = {-2.0, 4.0, -3.0, 1.0};

        imsl_f_zeros_poly(NDEG, coeff,
                          IMSL_RETURN_USER, zeros, 0);

        imsl_c_write_matrix ("The complex zeros found are", 1, 3,
            zeros, 0);
}

Output

                       The complex zeros found are
                      1                        2                        3
(         1,         0)  (         1,         1)  (         1,        -1)

Warning Errors

IMSL_ZERO_COEFF                                     The first several coefficients of the polynomial are equal to zero. Several of the last roots will be set to machine infinity to compensate for this problem.

IMSL_FEWER_ZEROS_FOUND                     Fewer than ndeg zeros were found. The root vector will contain the value for machine infinity in the locations that do not contain zeros.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260