Analyzes a one-way classification model.
Synopsis
#include <imsls.h>
float imsls_f_anova_oneway (int n_groups, int n[], float y[], ..., 0)
The type double function is imsls_d_anova_oneway
Required Arguments
int n_groups
(Input)
Number of groups.
int n[]
(Input)
Array of length n_groups containing
the number of responses for each group.
float y[]
(Input)
Array of length n [0] + n [1] + … + n [n_group − 1] containing the
responses for each group.
Return Value
The p-value for the F-statistic.
Synopsis with Optional Arguments
#include <imsls.h>
float
imsls_f_anova_oneway (int
n_groups, int n[], float
y[],
IMSLS_ANOVA_TABLE, float
**anova_table,
IMSLS_ANOVA_TABLE_USER, float
anova_table[],
IMSLS_GROUP_MEANS, float
**means,
IMSLS_GROUP_MEANS_USER, float
means[],
IMSLS_GROUP_STD_DEVS, float
**std_devs,
IMSLS_GROUP_STD_DEVS_USER, float
std_devs[],
IMSLS_GROUP_COUNTS, int
**counts,
IMSLS_GROUP_COUNTS_USER, int counts[],
IMSLS_CONFIDENCE, float confidence,
IMSLS_TUKEY, float
**ci_diff_means,
or
IMSLS_DUNN_SIDAK, float
**ci_diff_means,
or
IMSLS_BONFERRONI, float
**ci_diff_means,
or
IMSLS_SCHEFFE, float
**ci_diff_means,
or
IMSLS_ONE_AT_A_TIME, float
**ci_diff_means,
IMSLS_TUKEY_USER, float
ci_diff_means[],
or
IMSLS_DUNN_SIDAK_USER, float
ci_diff_means[],
or
IMSLS_BONFERRONI_USER, float
ci_diff_means[],
or
IMSLS_SCHEFFE_USER, float
ci_diff_means[],
or
IMSLS_ONE_AT_A_TIME_USER, float
ci_diff_means[],
0)
Optional Arguments
IMSLS_ANOVA_TABLE, float
**anova_table (Output)
Address of a pointer to an
internally allocated array of size 15 containing the analysis of variance table.
The analysis of variance statistics are as follows:
|
Element |
Analysis of Variance Statistics |
|
0 |
degrees of freedom for the model |
|
1 |
degrees of freedom for error |
|
2 |
total (corrected) degrees of freedom |
|
3 |
sum of squares for the model |
|
4 |
sum of squares for error |
|
5 |
total (corrected) sum of squares |
|
6 |
model mean square |
|
7 |
error mean square |
|
8 |
overall F-statistic |
|
9 |
p-value |
|
10 |
R2 (in percent) |
|
11 |
adjusted R2 (in percent) |
|
12 |
estimate of the standard deviation |
|
13 |
overall mean of y |
|
14 |
coefficient of variation (in percent) |
IMSLS_ANOVA_TABLE_USER, float
anova_table[] (Output)
Storage for array anova_table is
provided by the user. See IMSLS_ANOVA_TABLE.
IMSLS_GROUP_MEANS, float **means
(Output)
Address of a pointer to an internally allocated array of length
n_groups
containing the group means.
IMSLS_GROUP_MEANS_USER, float means[]
(Output)
Storage for array means is provided by
the user. See IMSLS_GROUP_MEANS.
IMSLS_GROUP_STD_DEVS, float
**std_devs (Output)
Address of a pointer to an internally
allocated array of length n_groups containing
the group standard deviations.
IMSLS_GROUP_STD_DEVS_USER, float
std_devs[] (Output)
Storage for array std_devs is provided
by the user. See IMSLS_STD_DEVS.
IMSLS_GROUP_COUNTS, int **counts
(Output)
Address of a pointer to an internally allocated array of length
n_groups
containing the number of nonmissing observations for the groups.
IMSLS_GROUP_COUNTS_USER, int counts[]
(Output)
Storage for array counts is provided by
the user. See IMSLS_COUNTS.
IMSLS_CONFIDENCE, float
confidence (Input)
Confidence level for the simultaneous
interval estimation.
If IMSLS_TUKEY is
specified, confidence must be in
the range [90.0, 99.0). Otherwise, confidence is in the range
[0.0, 100.0).
Default: confidence = 95.0
IMSLS_TUKEY, float **ci_diff_means (Output), or
IMSLS_DUNN_SIDAK, float **ci_diff_means (Output), or
IMSLS_BONFERRONI, float **ci_diff_means (Output), or
IMSLS_SCHEFFE, float **ci_diff_means (Output), or
IMSLS_ONE_AT_A_TIME, float
**ci_diff_means (Output)
Function imsls_f_anova_oneway
computes the confidence intervals on all pairwise differences of means using any
one of six methods: Tukey, Tukey-Kramer, Dunn-Šidák, Bonferroni, Scheffé, or
Fisher’s LSD (One-at-a-Time). If IMSLS_TUKEY is
specified, the Tukey confidence intervals are calculated if the group sizes are
equal; otherwise, the Tukey-Kramer confidence intervals are calculated.
On return, ci_diff_means contains the address of a pointer to a

internally allocated array containing the statistics relating to the difference of means.
|
Column |
Description |
|
0 |
group number for the i-th mean |
|
1 |
group number for the j-th mean |
|
2 |
difference of means (i-th mean) − (j-th mean) |
|
3 |
lower confidence limit for the difference |
|
4 |
upper confidence limit for the difference |
IMSLS_TUKEY_USER, float ci_diff_means[] (Output), or
IMSLS_DUNN_SIDAK_USER, float ci_diff_means[] (Output), or
IMSLS_BONFERRONI_USER, float ci_diff_means[] (Output), or
IMSLS_SCHEFFE_USER, float ci_diff_means[] (Output), or
IMSLS_ONE_AT_A_TIME_USER, float ci_diff_means[]
(Output)
Storage for array ci_diff_means is
provided by the user.
Description
Function imsls_f_anova_oneway performs an analysis of variance of responses from a oneway classification design. The model is
yij = μi + ɛij i = 1, 2, …, k; j = 1, 2, …, ni
where the observed value yij constitutes the
j-th response in the i-th group,
μi denotes the population
mean for the i-th group, and the ɛij arguments are errors
that are identically and independently distributed normal with mean 0 and
variance σ2. Function imsls_f_anova_oneway
requires the yij observed responses as
input into a single vector y with responses in each group occupying
contiguous locations. The analysis of variance table is computed along with the
group sample means and standard deviations. A discussion of formulas and
interpretations for the one-way analysis of variance problem appears in most
elementary statistics texts, e.g., Snedecor and Cochran (1967, Chapter
10).
Function imsls_f_anova_oneway computes simultaneous confidence intervals on all
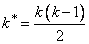
pairwise comparisons of k means μ1 μ2, …, μk in the one-way analysis of variance model. Any of several methods can be chosen. A good review of these methods is given by Stoline (1981). The methods are also discussed in many elementary statistics texts, e.g., Kirk (1982, pp. 114−127).
Let s2 be the estimated variance of a single observation. Let v be the degrees of freedom associated with s2. Let
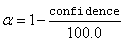
The methods are summarized as follows:
Tukey method: The Tukey method gives the narrowest
simultaneous confidence intervals for all pairwise differences of means μi − μj in balanced
(n1 = n2 = … = nk = n)
one-way designs. The method is exact and uses the Studentized range
distribution. The formula for the difference μi − μj is given by
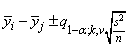
where q1−a;k,v is the (1 − α) 100 percentage point of the Studentized range distribution with parameters k and v.
Tukey-Kramer method: The Tukey-Kramer method is an approximate extension of the Tukey method for the unbalanced case. (The method simplifies to the Tukey method for the balanced case.) The method always produces confidence intervals narrower than the Dunn-Šidák and Bonferroni methods. Hayter (1984) proved that the method is conservative, i.e., the method guarantees a confidence coverage of at least (1 − α) 100. Hayter’s proof gave further support to earlier recommendations for its use (Stoline 1981). (Methods that are currently better are restricted to special cases and only offer improvement in severely unbalanced cases; see, for example, Spurrier and Isham 1985.) The formula for the difference μi − μj is given by the following:
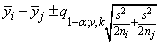
Dunn-Šidák method: The Dunn-Šidák method is a conservative method. The method gives wider intervals than the Tukey-Kramer method. (For large v and small α and k, the difference is only slight.) The method is slightly better than the Bonferroni method and is based on an improved Bonferroni (multiplicative) inequality (Miller 1980, pp. 101, 254−255). The method uses the t distribution (see function imsls_f_t_inverse_cdf, Chapter 11, “Probability Distribution Functions and Inverses. The formula for the difference μi − μj is given by
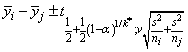
where tf ;v is the 100f percentage point of the t distribution with ν degrees of freedom.
Bonferroni method: The Bonferroni method is a conservative method based on the Bonferroni (additive) inequality (Miller, p. 8). The method uses the t distribution. The formula for the difference μi − μj is given by the following:
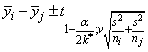
Scheffé method: The Scheffé method is an overly conservative method for simultaneous confidence intervals on pairwise difference of means. The method is applicable for simultaneous confidence intervals on all contrasts, i.e., all linear combinations
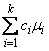
where the following is true:
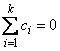
This method can be recommended here only if a large number of confidence intervals on contrasts in addition to the pairwise differences of means are to be constructed. The method uses the F distribution (see function imsls_f_F_inverse_cdf, Chapter 11, “Probabilty and Distribution Functions and Inverses”.p<.CSCH11.DOC!F_INVERSE_CDF;507;). The formula for the difference μi − μj is given by
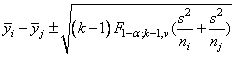
where F1−a; ( k−1),v is the (1 − α) 100 percentage point
of the F distribution with
k − 1 and ν degrees of freedom.
One-at-a-Time t method (Fisher’s LSD): The
One-at-a-Time t method is appropriate for constructing a single
confidence interval. The confidence percentage input is appropriate for one
interval at a time. The method has been used widely in conjunction with the
overall test of the null hypothesis
μ1 = μ2 = … = μk by the use of the
F statistic. Fisher’s LSD (least significant difference) test is a
two-stage test that proceeds to make pairwise comparisons of means only if the
overall F test is significant. Milliken and Johnson (1984, p.
31) recommend LSD comparisons after a significant F only if the number of
comparisons is small and the comparisons were planned prior to the analysis. If
many unplanned comparisons are made, they recommend Scheffé’s method. If the
F test is insignificant, a few planned comparisons for differences in
means can still be performed by using either Tukey, Tukey-Kramer, Dunn-Šidák,or
Bonferroni methods. Because the F test is insignificant, Scheffé’s method
does not yield any significant differences. The formula for the difference μi − μj is given by the
following:
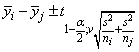
Examples
Example 1
This example computes a one-way analysis of variance for data discussed by Searle (1971, Table 5.1, pp. 165−179). The responses are plant weights for six plants of three different types—three normal, two off-types, and one aberrant. The responses are given by type of plant in the following table:
|
Normal |
Off-Type |
Aberrant |
|
101 |
84 |
32 |
|
105 |
88 |
|
|
94 |
|
|
#include
<imsls.h>
main()
{
int
n_groups=3;
int n[] = {3, 2,
1};
float y[] = {101.0, 105.0, 94.0, 84.0,
88.0, 32.0};
float
p_value;
p_value = imsls_f_anova_oneway (n_groups, n, y,
0);
printf ("p-value = %6.4f", p_value);
}
Output
p-value = 0.002
Example 2
The data used in this example is the same as that used in the initial example. Here, the anova_table is printed.
#include
<imsls.h>
main()
{
int
n_groups=3;
int n[] = {3, 2,
1};
float y[] = {101.0, 105.0, 94.0, 84.0,
88.0, 32.0};
float
p_value;
float
*anova_table;
char *labels[] =
{
"degrees of freedom for among
groups",
"degrees of freedom for within
groups",
"total (corrected) degrees of
freedom",
"sum of squares for among
groups",
"sum of squares for within
groups",
"total (corrected) sum of
squares",
"among mean
square",
"within mean square",
"F-statistic",
"p-value", "R-squared (in
percent)",
"adjusted R-squared (in
percent)",
"est. standard deviation of within
error",
"overall mean of
y",
"coefficient of variation (in
percent)"};
/* Perform analysis */
p_value = imsls_f_anova_oneway
(n_groups, n, y,
IMSLS_ANOVA_TABLE,
&anova_table,
0);
/* Print results */
imsls_f_write_matrix("* * *
Analysis of Variance * * *\n", 15,
1,
anova_table,
IMSLS_ROW_LABELS,
labels,
IMSLS_WRITE_FORMAT,
"%9.2f",
0);
}
Output
* * *
Analysis of Variance * * *
degrees of freedom for among
groups
2.00
degrees of freedom for within
groups 3.00
total
(corrected) degrees of
freedom 5.00
sum of
squares for among
groups
3480.00
sum of squares for within
groups
70.00
total (corrected) sum of
squares
3550.00
among mean
square
1740.00
within mean
square
23.33
F-statistic
74.57
p-value
0.00
R-squared (in
percent)
98.03
adjusted R-squared (in
percent)
96.71
est. standard deviation of within
error 4.83
overall mean of
y
84.00
coefficient of variation (in
percent) 5.75
Example 3
Simultaneous confidence intervals are generated for the following measurements of cold-cranking power for five models of automobile batteries. Nelson (1989, pp. 232−241) provided the data and approach.
|
Model 1 |
Model 2 |
Model 3 |
Model 4 |
Model 5 |
|
41 |
42 |
27 |
48 |
28 |
|
43 |
43 |
26 |
45 |
32 |
|
42 |
46 |
28 |
51 |
37 |
|
46 |
38 |
27 |
46 |
25 |
The Tukey method is chosen for the analysis of pairwise comparisons, with a confidence level of 99 percent. The means and their confidence limits are output.
#include <imsls.h>
void
main()
{
int n_groups =
5;
int n[] = {4, 4, 4, 4, 4};
int permute[] = {2, 3, 4, 0, 1};
float
y[] = {41.0, 43.0, 42.0, 46.0, 42.0,
43.0, 46.0, 38.0, 27.0,
26.0,
28.0, 27.0, 48.0, 45.0,
51.0,
46.0, 28.0, 32.0, 37.0, 25.0};
float *anova_table,
*ci_diff_means, tmp_diff_means[50];
float confidence =
99.0;
char *labels[] =
{
"degrees of freedom for among
groups",
"degrees of freedom for within
groups",
"total (corrected) degrees of
freedom",
"sum of squares for among
groups",
"sum of squares for within groups",
"total
(corrected) sum of
squares",
"among mean
square",
"within mean square",
"F-statistic",
"p-value", "R-squared (in
percent)",
"adjusted R-squared (in
percent)",
"est. standard deviation of within
error",
"overall mean of
y",
"coefficient of variation (in percent)"};
char
*mean_row_labels[] =
{
"first and second",
"first and
third",
"first and
fourth",
"first and
fifth",
"second and
third",
"second and
fourth",
"second and
fifth",
"third and
fourth",
"third and
fifth",
"fourth and fifth"};
char *mean_col_labels[] =
{
"Means",
"Difference of
means",
"Lower
limit",
"Upper
limit"};
/* Perform analysis */
imsls_f_anova_oneway(n_groups,
n, y,
IMSLS_ANOVA_TABLE,
&anova_table,
IMSLS_CONFIDENCE, confidence,
IMSLS_TUKEY, &ci_diff_means,
0);
/* Print anova_table */
imsls_f_write_matrix("* * *
Analysis of Variance * * *\n", 15,
1, anova_table,
IMSLS_ROW_LABELS,
labels,
IMSLS_WRITE_FORMAT,
"%9.2f",
0);
/* Permute ci_diff_means for printing */
imsls_f_permute_matrix(10, 5, ci_diff_means,
permute,
IMSLS_PERMUTE_COLUMNS,
IMSLS_RETURN_USER, tmp_diff_means,
0);
/* Print ci_diff_means */
imsls_f_write_matrix("* * *
Differences in Means * * *\n", 10,
3, tmp_diff_means,
IMSLS_A_COL_DIM, 5,
IMSLS_ROW_LABELS, mean_row_labels,
IMSLS_COL_LABELS, mean_col_labels,
IMSLS_WRITE_FORMAT, "%9.2f",
0);
}
Output
* * *
Analysis of Variance * * *
degrees of freedom for among
groups
4.00
degrees of freedom for within
groups 15.00
total
(corrected) degrees of freedom
19.00
sum of squares for among
groups
1242.20
sum of squares for within
groups
150.75
total (corrected) sum of
squares
1392.95
among mean
square
310.55
within mean
square
10.05
F-statistic
30.90
p-value
0.00
R-squared (in
percent)
89.18
adjusted R-squared (in
percent)
86.29
est. standard deviation of within
error 3.17
overall mean of
y
38.05
coefficient of variation (in
percent)
8.33
*
* * Differences in Means * *
*
Means
Difference Lower limit Upper
limit
of
means
first and second
0.75
-8.05 9.55
first and
third
16.00
7.20 24.80
first and
fourth
-4.50
-13.30 4.30
first and
fifth
12.50
3.70 21.30
second and
third
15.25
6.45 24.05
second and
fourth
-5.25
-14.05 3.55
second and
fifth
11.75
2.95 20.55
third and
fourth
-20.50
-29.30 -11.70
third and
fifth
-3.50
-12.30 5.30
fourth and
fifth
17.00
8.20 25.80
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |