Computes forecasts and their associated probability limits for an ARMA model.
Synopsis
#include <imsls.h>
float *imsls_f_arma_forecast (Imsls_f_arma *arma_info, int n_predict, ..., 0)
The type double function is imsls_d_arma_forecast.
Required Arguments
Imsls_f_arma
*arma_info (Input)
Pointer to a structure of type
Imsls_f_arma that is passed from the imsls_f_arma
function.
int n_predict
(Input)
Maximum lead time for forecasts. Argument n_predict must be
greater than 0.
Return Value
Pointer to an array of length n_predict × (backward_origin + 3) containing the forecasts up to n_predict steps ahead and the information necessary to obtain pairwise confidence intervals. More information is given in the description of argument IMSLS_RETURN_USER.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_arma_forecast (Imsls_f_arma
*arma_info,
int n_predict,
IMSLS_CONFIDENCE, float
confidence,
IMSLS_BACKWARD_ORIGIN, int
backward_origin,
IMSLS_RETURN_USER, float
forecasts[],
0)
Optional Arguments
IMSLS_CONFIDENCE, float
confidence (Input)
Value in the exclusive interval (0,
100) used to specify the confidence percent
probability limits of the forecasts. Typical choices for confidence are 90.0,
95.0, and 99.0.
Default: confidence = 95.0
IMSLS_BACKWARD_ORIGIN, int
backward_origin (Input)
If specified, the maximum backward
origin. Argument backward_origin must
be greater than or equal to 0 and less than or equal to n_observations − max (maxar,
maxma), where maxar = max (ar_lags [i]),
maxma = max (ma_lags [j]),
and n_observations = the
number of observations in the series, as input in function imsls_f_arma. Forecasts at origins n_observations − backward_origin
through n_observations are
generated.
Default: backward_origin = 0
IMSLS_RETURN_USER, float
forecasts[] (Output)
If specified, a user-specified array
of length
n_predict × (backward_origin + 3)
as defined below.
|
Column |
Content |
|
J |
forecasts for lead times l = 1, ..., n_predict at origins n_observations − backward_origin − 1 + j, where j = 0, ..., backward_origin |
|
backward_origin + 2 |
deviations from each forecast that give the confidence percent probability limits |
|
backward_origin + 3 |
psi weights of the infinite order moving average form of the model |
If specified, the forecasts for lead times l = 1, ..., n_predict at origins n_observations − backward_origin − 1 + j, where j = 1, ..., backward_origin + 1.
Description
The Box-Jenkins forecasts and their associated probability
limits for a nonseasonal ARMA model are computed given a sample of
n = n_observations
{Zt} for
t = 1, 2, ..., n, where n_observations = the
number of observations in the series, as input in function imsls_f_arma.
Suppose the time series {Zt} is generated by a nonseasonal ARMA model of the form
ɸ(B)Zt = θ0 + θ(B)At
for t ∈ {0, ±1, ±2, ...}, where B is the backward shift operator, θ0 is the constant, and
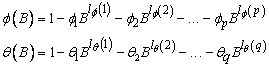
with p autoregressive and q moving average parameters. Without loss of generality, the following is assumed:
1 ≤ lf (1) ≤ lf (2) ≤ … ≤ lf (p)
1 ≤ lq (1) ≤ lq (2) ≤ … ≤ lq (q)
so that the nonseasonal ARMA model is of order (pʹ, qʹ), where pʹ = lq(p) and qʹ = lq(q). Note that the usual hierarchical model assumes the following:
lf (i) = i, 1 ≤ i ≤ p
lq (j) = j, 1 ≤ j ≤ q
The Box-Jenkins forecast at origin t for lead time l of Zt+1 is defined in terms of the difference equation
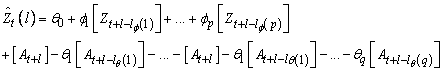
where the following is true:
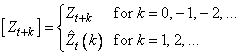
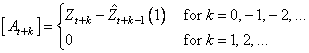
The 100(1 − α) percent probability limits for Zt+1 are given by
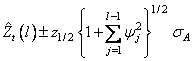
where z(1−a∕2) is the 100(1 − α/2) percentile of the standard normal distribution
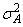
(returned from imsls_f_arma) and
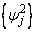
are the parameters of the random shock form of the
difference equation. Note that the forecasts are computed for lead times
l = 1, 2, ..., L at origins
t = (n − b),
(n − b + 1),
..., n, where L = n_predict
and b = backward_origin.
The Box-Jenkins forecasts minimize the mean-square error
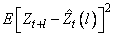
Also, the forecasts can be easily updated according to the following equation:
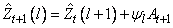
This approach and others are discussed in Chapter 5: “Forecasting” of Box and Jenkins (1976).
Example
Consider the Wolfer Sunspot Data (Anderson 1971, p. 660)
consisting of the number of sunspots observed each year from 1749 through 1924.
The data set for this example consists of the number of sunspots observed from
1770 through 1869. Function imsls_f_arma_forecast
computes forecasts and 95-percent probability limits for the forecasts for an
ARMA(2, 1) model fit using function imsls_f_max_arma
with the method of moments option. With backward_origin = 3,
columns zero through three of forecasts
provide forecasts given the data through 1866, 1867, 1868, and 1869,
respectively. Column four gives the deviations from the forecast for computing
probability limits, and column six gives the psi weights, which can be used to
update forecasts when more data is available. For example, the forecast for the
102nd observation (year 1871) given the data through the 100th observation (year
1869) is 77.21; and 95-percent probability limits are given by 77.21 56.30. After observation 101 (
Z101 for year 1870) is
available, the forecast can be updated by using
56.30. After observation 101 (
Z101 for year 1870) is
available, the forecast can be updated by using
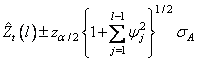
with the psi weight (Ψ1 = 1.37) and the one-step-ahead forecast error for observation 101 (Z101 − 83.72) to give the following:
77.21 + 1.37 × (Z101 − 83.72)
Since this updated forecast is one step ahead, the
95-percent probability limits are now given by the forecast  33.22.
33.22.
#include <imsls.h>
void main()
{
int p = 2;
int q = 1;
int i;
int n_observations = 100;
int max_iterations = 0;
int n_predict = 12;
int backward_origin = 3;
float w[176][2];
float z[100];
float *parameters;
float rel_error = 0.0;
float *forecasts;
Imsls_f_arma *arma_info;
char *col_labels[] = {
"Lead Time",
"Forecast From 1866",
"Forecast From 1867",
"Forecast From 1868",
"Forecast From 1869",
"Dev. for Prob. Limits",
"Psi"};
imsls_f_data_sets(2, IMSLS_X_COL_DIM,
2, IMSLS_RETURN_USER, w,
0);
for (i=0; i<n_observations; i++) z[i] = w[21+i][1];
parameters = imsls_f_arma(n_observations, &z[0], p, q,
IMSLS_RELATIVE_ERROR,
rel_error,
IMSLS_MAX_ITERATIONS,
max_iterations,
IMSLS_ARMA_INFO,
&arma_info,
0);
printf("Method of Moments initial estimates:\n");
printf("AR estimates are %11.4f and %11.4f.\n",
parameters[1], parameters[2]);
printf("MA estimate is %11.4f.\n", parameters[3]);
forecasts =
imsls_f_arma_forecast(arma_info, n_predict,
IMSLS_BACKWARD_ORIGIN,
backward_origin,
0);
imsls_f_write_matrix("* * * Forecast Table * * *\n",
n_predict, backward_origin+3,
forecasts,
IMSLS_COL_LABELS, col_labels,
IMSLS_WRITE_FORMAT, "%11.4f",
0);
}
Output
Method of Moments initial estimates:
AR estimates are 1.2443 and -0.5751.
MA estimate is -0.1241.
* * * Forecast Table * * *
Lead Time Forecast From Forecast From
Forecast From Forecast From
1866 1867 1868 1869
1 18.2833 16.6151 55.1893 83.7196
2 28.9182 32.0189 62.7606 77.2092
3 41.0101 45.8275 61.8922 63.4608
4 49.9387 54.1496 56.4571 50.0987
5 54.0937 56.5623 50.1939 41.3803
6 54.1282 54.7780 45.5268 38.2174
7 51.7815 51.1701 43.3221 39.2965
8 48.8417 47.7072 43.2631 42.4582
9 46.5335 45.4736 44.4577 45.7715
10 45.3524 44.6861 45.9781 48.0758
11 45.2103 44.9909 47.1827 49.0371
12 45.7128 45.8230 47.8072 48.9080
Lead Time Dev. for Prob. Psi
Limits
1 33.2179 1.3684
2 56.2980 1.1274
3 67.6168 0.6158
4 70.6432 0.1178
5 70.7515 -0.2076
6 71.0869 -0.3261
7 71.9074 -0.2863
8 72.5337 -0.1687
9 72.7498 -0.0452
10 72.7653 0.0407
11 72.7779 0.0767
12 72.8225 0.0720
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |