Chapter 8: Time Series and Forecasting

autocorrelation

Computes the sample autocorrelation function of a stationary time series.

Synopsis

#include <imsls.h>

float *imsls_f_autocorrelation (int n_observations, float x[],
int lagmax, ...
0)

The type double function is imsls_d_autocorrelation.

Required Arguments

int n_observations  (Input)
Number of observations in the time series x.  n_observations must be greater than or equal to 2.

float x[]  (Input)
Array of length n_observations containing the time series.

int lagmax  (Input)
Maximum lag of autocovariance, autocorrelations, and standard errors of autocorrelations to be computed.  lagmax must be greater than or equal to 1 and less than n_observations.

Return Value

Pointer to an array of length lagmax + 1 containing the autocorrelations of the time series x.  The 0-th element of this array is 1.  The k-th element of this array contains the autocorrelation of lag k where k = 1, ..., lagmax.

Synopsis with Optional Arguments

 

#include <imsls.h>

float imsls_f_autocorrelation (int n_observations, float x[],
int lagmax,
IMSLS_RETURN_USER,  float autocorrelations[],
IMSLS_PRINT_LEVEL, int iprint,
IMSLS_ACV, float **autocovariances,
IMSLS_ACV_USER, float autocovariances[],
IMSLS_SEAC, float **standard_errors,
int se_option,
IMSLS_SEAC_USER, float standard_errors[],
int se_option,
IMSLS_X_MEAN_IN, float x_mean_in,
IMSLS_X_MEAN_OUT, float *x_mean_out,
0)

Optional Arguments

IMSLS_RETURN_USER,  float autocorrelations[]  (Output)
If specified, autocorrelations is an array of length lagmax + 1 containing the autocorrelations of the time series x. The
oth element of this array is 1.  The kth element of this array contains the autocorrelation of lag k where k = 1, ..., lagmax.

IMSLS_PRINT_LEVEL, int iprint  (Input)
Printing option. 
Default = 0.

Iprint

Action

0

No printing is performed.

1

Prints the mean and variance.

2

Prints the mean, variance, and autocovariances.

3

Prints the mean, variance, autocovariances, autocorrelations, and standard errors of autocorrelations.

IMSLS_ACV, float **autocovariances  (Output)
Address of a pointer to an array of length lagmax + 1 containing the variance and autocovariances of the time series x.  The 0-th element of this array is the variance of the time series x.  The kth element contains the autocovariance of lag k where k = 1, ..., lagmax.

IMSLS_ACV_USER, float autocovariances[]  (Output)
If specified, autocovariances is an array of length lagmax + 1 containing the variance and autocovariances of the time series x. 
See IMSLS_ACV.

IMSLS_SEAC, float **standard_errors, int se_option  (Output)
Address of a pointer to an array of length lagmax containing the standard errors of the autocorrelations of the time series x.
Method of computation for standard errors of the autocorrelations is chosen by se_option.

se_option

Action

1

Compute the standard errors of autocorrelations using Barlett’s formula.

2

Compute the standard errors of autocorrelations using Moran’s formula.

         

IMSLS_SEAC_USER, float standard_errors[], int se_option  (Output)
If specified, autocovariances is an array of length lagmax containing the standard errors of the autocorrelations of the time series x.
See IMSLS_SEAC.

IMSLS_X_MEAN_IN, float x_mean_in  (Input)
User input the estimate of the time series x.

IMSLS_X_MEAN_OUT, float *x_mean_out  (Output)
If specified, x_mean_out is the estimate of the mean of the time
series x.

Description

Function imsls_f_autocorrelation estimates the autocorrelation function of a stationary time series given a sample of  n  =  n_observations observations {Xt} for t = 1, 2, …, n.

Let

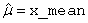
be the estimate of the mean m of the time series {Xt} where

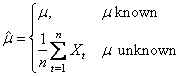
The autocovariance function s(k) is estimated by

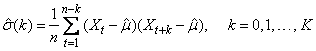
where K = lagmax. Note that

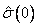
is an estimate of the sample variance. The autocorrelation function ρ(k) is estimated by

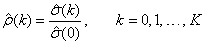
Note that

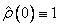
by definition.

The standard errors of the sample autocorrelations may be optionally computed according to argument se_option for the optional argument IMSLS_SEAC. One method (Bartlett 1946) is based on a general asymptotic expression for the variance of the sample autocorrelation coefficient of a stationary time series with independent, identically distributed normal errors. The theoretical formula is

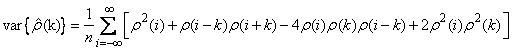
where

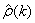
assumes m is unknown. For computational purposes, the autocorrelations r(k) are replaced by their estimates

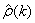
for |k| £ K, and the limits of summation are bounded because of the assumption that
r(k) = 0 for all k such that |k| > K.

A second method (Moran 1947) utilizes an exact formula for the variance of the sample autocorrelation coefficient of a random process with independent, identically distributed normal errors. The theoretical formula is

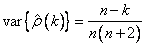
where m is assumed to be equal to zero. Note that this formula does not depend on the autocorrelation function.

Example

Consider the Wolfer Sunspot Data (Anderson 1971, page 660) consisting of the number of sunspots observed each year from 1749 through 1924. The data set for this example consists of the number of sunspots observed from 1770 through 1869. Function imsls_f_autocorrelation with optional arguments computes the estimated autocovariances, estimated autocorrelations, and estimated standard errors of the autocorrelations.

#include <imsls.h>

#include <stdio.h>

 

void main()

{

   float *result=NULL, data[176][2], x[100], xmean;

   int i, nobs = 100, lagmax = 20;

   float *acv=NULL, *seac=NULL;

 

 

   imsls_f_data_sets(2, IMSLS_RETURN_USER, data, 0);

   for (i=0;i<nobs;i++) x[i] = data[21+i][1];

 

   result = imsls_f_autocorrelation(nobs, x, lagmax,

                            IMSLS_X_MEAN_OUT, &xmean,

                            IMSLS_ACV, &acv,

                            IMSLS_SEAC, &seac, 1,
                            0);   

   printf("Mean     = %8.3f\n", xmean);

   printf("Variance = %8.1f\n", acv[0]);

   printf("\nLag\t   ACV\t\t   AC\t\t   SEAC\n");

   printf("%2d\t%8.1f\t%8.5f\n", 0, acv[0], result[0]);

   for(i=1; i<21; i++)

      printf("%2d\t%8.1f\t%8.5f\t%8.5f\n", i, acv[i], result[i],

      seac[i-1]);

     

}

Output

 

Mean     =     46.976
Variance =     1382.9

Lag         ACV           AC          SEAC

 0         1382.9      1.00000
 1         1115.0      0.80629      0.03478
 2          592.0      0.42809      0.09624
 3           95.3      0.06891      0.15678
 4         -236.0     -0.17062      0.20577
 5         -370.0     -0.26756      0.23096
 6         -294.3     -0.21278      0.22899
 7          -60.4     -0.04371      0.20862
 8          227.6      0.16460      0.17848
 9          458.4      0.33146      0.14573
10          567.8      0.41061      0.13441
11          546.1      0.39491      0.15068
12          398.9      0.28848      0.17435
13          197.8      0.14300      0.19062
14           26.9      0.01945      0.19549
15          -77.3     -0.05588      0.19589
16         -143.7     -0.10394      0.19629
17         -202.0     -0.14610      0.19602
18         -245.4     -0.17743      0.19872
19         -230.8     -0.16691      0.20536
20         -142.9     -0.10332      0.20939

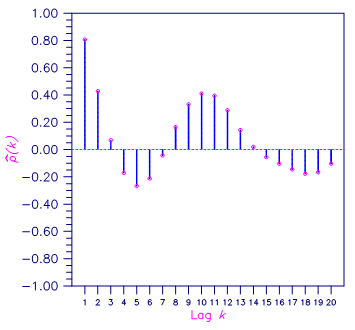
Figure 8-1 Sample Autocorrelation Function

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260