Evaluates the gamma distribution function.

Synopsis

#include <imsls.h>

float imsls_f_gamma_cdf (float x, float a)

The type double function is imsls_d_gamma_cdf.

Required Arguments

float x   (Input)
Argument for which the gamma distribution function is to be evaluated.

float a   (Input)
Shape parameter of the gamma distribution. This parameter must be positive.

Return Value

The probability that a gamma random variable takes a value less than or equal to x.

Description

Function imsls_f_gamma_cdf evaluates the distribution function, F, of a gamma random variable with shape parameter a,

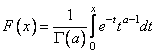
where Γ(×) is the gamma function. (The gamma function is the integral from 0 to ¥ of the same integrand as above.) The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

The gamma distribution is often defined as a two-parameter distribution with a scale parameter b (which must be positive) or as a three-parameter distribution in which the third parameter c is a location parameter. In the most general case, the probability density function over (c, ¥) is as follows:

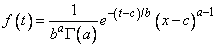
If T is a random variable with parameters a, b, and c, the probability that T ≤ t0 can be obtained from imsls_f_gamma_cdf by setting x = (t0 − c)/b.

If x is less than a or less than or equal to 1.0, imsls_f_gamma_cdf uses a
series expansion; otherwise, a continued fraction expansion is used.
(See Abramowitz and Stegun 1964.)

Example

Let X be a gamma random variable with a shape parameter of four. (In this case, it has an Erlang distribution since the shape parameter is an integer.) This example finds the probability that X is less than 0.5 and the probability that
X is between 0.5 and 1.0.

#include <imsls.h>

main()
{
    float       p, x;
    float       a = 4.0;

    x = 0.5;
    p = imsls_f_gamma_cdf(x,a);
    printf("The probability that X is less than 0.5 is %6.4f\n", p);

    x = 1.0;
    p = imsls_f_gamma_cdf(x,a) - p;
    printf("The probability that X is between 0.5 and 1.0 is %6.4f\n",
        p);
}

Output

The probability that X is less than 0.5 is 0.0018
The probability that X is between 0.5 and 1.0 is 0.0172

Informational Errors

IMSLS_ARG_LESS_THAN_ZERO                Since “x” = # is less than zero, the distribution function is zero at “x.”

Fatal Errors

IMSLS_X_AND_A_TOO_LARGE                  Since “x” = # and “a” = # are so large, the algorithm would overflow.

 

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260