Conducts Bartlett’s and Levene’s tests of the homogeneity of variance assumption in analysis of variance.
Synopsis
#include <imsls.h>
float * imsls_f_homogeneity (int n, int n_treatment, int treatment[], float y[],…, 0)
The type double is imsls_d_homogeneity.
Required Arguments
int n
(Input)
Number of experimental observations.
int n_treatment
(Input)
Number of treatments. n_treatment must be
greater than one.
int treatment[]
(Input)
An array of length n containing the
treatment identifiers for each observation in y. Each level of
the treatment must be assigned a different integer. imsls_f_homogeneity
verifies that the number of unique treatment identifiers is equal to n_treatment.
float y[] (Input)
An
array of length n containing the
experimental observations and any missing values. Missing values can be
included in this array, although they are ignored in the analysis. They
are indicated by placing a NaN (not a number) in y. The NaN value can
be set using either the function imsls_f_machine(6) or
imsls_d_machine(6),
depending upon whether single or double precision is being used,
respectively.
Return Value
Address of a pointer to the memory location of an array of length 2 containing the p-values for Bartletts and Levene’s tests.
Synopsis with Optional Arugments
#include <imsl.h>
float *
imsls_f_homogeneity (int
n, int n_treatment,
int n_treatment[],
float y[],
IMSLS_RETURN_USER, float
p_value[]
IMSLS_LEVENES_MEAN or
IMSLS_LEVENES_MEDIAN,
IMSLS_N_MISSING,
int *n_missing,
IMSLS_CV, float
*cv,
IMSLS_GRAND_MEAN, float
*grand_mean,
IMSLS_TREATMENT_MEANS, float
**treatment_means,
IMSLS_TREATMENT_MEANS_USER, float
treatment_means[],
IMSLS_RESIDUALS, float
**residuals,
IMSLS_RESIDUALS_USER, float
residuals[],
IMSLS_STUDENTIZED_RESIDUALS,
float
**studentized_residuals,
IMSLS_STUDENTIZED_RESIDUALS_USER,
float
studentized_residuals[],
IMSLS_STD_DEVS, float
**std_devs,
IMSLS_STD_DEVS_USER, float std_devs[],
IMSLS_BARTLETTS,
float
*bartletts,
IMSLS_LEVENES, float *levenes,
0)
Optional Arguments
IMSLS_RETURN_USER,
float p_value[]
(Output)
User defined array of length 2 for storage of the p-values
from Bartlett’s and Levene’s tests for homogeneity of variance. The first
value returned contains the p-value for Bartlett’s test and the
second value contains the p-value for Levene’s test.
IMSLS_LEVENES_MEAN or
IMSLS_LEVENES_MEDIAN
(Input)
Calculates Levene’s test using either the treatment means or
medians. IMSLS_LEVENES_MEAN
indicates that Levene’s test is calculated using the mean, and IMSLS_LEVENES_MEDIAN
indicates that it is calculated using the median.
Default: IMSLS_LEVENES_MEAN
IMSLS_N_MISSING,
int
*n_missing
(Output)
Number of missing values, if any, found in
y.
Missing values are denoted with a NaN (Not a Number)
value in y. In these
analyses, any missing values are ignored.
IMSLS_CV, float
*cv
(Output)
The coefficient of variation computed using the grand mean
and pooled within treatment standard deviation.
IMSLS_GRAND_MEAN,
float grand_mean
(Output)
Mean of all the data across every location.
IMSLS_TREATMENT_MEANS,
float
**treatment_means (Output)
Address of a pointer to an
internally allocated array of size n_treatment containing
the treatment means.
IMSLS_TREATMENT_MEANS_USER,
float treatment_means[]
(Output)
Storage for the array treatment_means,
provided by the user.
IMSLS_RESIDUALS,
float
**residuals (Output)
Address of a pointer to an
internally allocated array of length n containing the
residuals for non-missing observations. The ordering of the values in this
array corresponds to the ordering of values in y and identified by
the values in treatments.
IMSLS_RESIDUALS_USER,
float residuals[]
(Output)
Storage for the array residuals, provided by
the user.
IMSLS_STUDENTIZED_RESIDUALS,
float **studentized_residuals
(Output)
Address of a pointer to an internally allocated array of
length n
containing the studentized residuals for non-missing observations. The
ordering of the values in this array corresponds to the ordering of values in
y and identified
by the values in treatments.
IMSLS_STUDENTIZED_RESIDUALS_USER,
float studentized_residuals[]
(Output)
Storage for the array studentized_residuals,
provided by the user.
IMSLS_STD_DEVS,
float
**std_devs (Output)
Address of a pointer to an
internally allocated array of length n_treatment containing
the treatment standard deviations.
IMSLS_STD_DEVS_USER,
float
std_devs[] (Output)
Storage for the array std_devs, provided by
the user.
IMSLS_BARTLETTS,
float *bartletts
(Output)
Test statistic for Bartlett’s test.
IMSLS_LEVENES,
float *levenes
(Output)
Test statistic for Levene’s test.
Description
Traditional analysis of variance assumes that variances within treatments are equal. This is referred to as homogeneity of variance. The function imsls_f_homogeneity conducts both the Bartlett’s and Levene’s tests for this assumption:
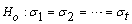
versus
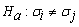
for at least one pair (iąj), where t=n_treatments.
Bartlett’s test, Bartlett (1937), uses the test statistic:
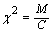
where

and 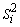 is the variance of the
is the variance of the 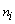 non-missing observations in the ith treatment.
non-missing observations in the ith treatment.
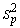 is referred to as the
pooled variance, and it is also known as the error mean squares from a 1-way
analysis of variance.
is referred to as the
pooled variance, and it is also known as the error mean squares from a 1-way
analysis of variance.
If the usual assumptions associated with the analysis of variance are valid, then Bartlett’s test statistic is a chi-squared random variable with degrees of freedom equal to t-1.
The original Levene’s test, Levene (1960) and Snedecor & Cochran (1967), uses a different test statistic, F0, equal to:
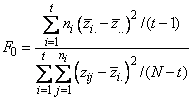 ,
,
where
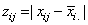 ,
,
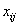 is
the jth observation from the ith treatment and
is
the jth observation from the ith treatment and 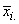 is the mean for the ith
treatment. Conover, Johnson, and Johnson (1981) compared over 50 similar
tests for homogeneity and concluded that one of the best tests was Levene’s test
when the treatment mean,
is the mean for the ith
treatment. Conover, Johnson, and Johnson (1981) compared over 50 similar
tests for homogeneity and concluded that one of the best tests was Levene’s test
when the treatment mean, 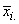 is replaced with the treatment median,
is replaced with the treatment median, 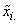 . This version of Levene’s
test can be requested by setting IMSLS_LEVENES_MEDIAN.
In either case, Levene’s test statistic is treated as a F random variable with
numerator degrees of freedom equal to (t-1) and denominator degrees of
freedom (N-t).
. This version of Levene’s
test can be requested by setting IMSLS_LEVENES_MEDIAN.
In either case, Levene’s test statistic is treated as a F random variable with
numerator degrees of freedom equal to (t-1) and denominator degrees of
freedom (N-t).
The residual for the jth observation within the ith
treatment, 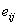 , returned
from IMSLS_RESIDUALS
is unstandarized, i.e.
, returned
from IMSLS_RESIDUALS
is unstandarized, i.e. 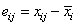 . For investigating problems of homogeneity of variance,
the studentized residuals returned by IMSLS_STUDENTIZED_RESIDUALS
are recommended since they are standarzied by the standard deviation of the
residual. The formula for calculating the studentized residual is:
. For investigating problems of homogeneity of variance,
the studentized residuals returned by IMSLS_STUDENTIZED_RESIDUALS
are recommended since they are standarzied by the standard deviation of the
residual. The formula for calculating the studentized residual is:
 ,
,
where the coefficient of variation, returned from IMSLS_CV,
is also calculated using the pooled variance and the grand mean  :
:
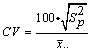
Example
This example applies Bartlett’s and Levene’s test to verify the homogeneity assumption for a one-way analysis of variance. There are eight treatments, each with 3 replicates for a total of 24 observations. The estimated treatment standard deviations range from 5.35 to 13.17.
In this case, Bartlett's test is not statistically significant for a stated significance level of .05; whereas Levene's test is significant with p = 0.006.
#include "imsls.h"
void ex_homog_b()
{
int i, page_width = 132;
int n = 24;
int n_treatment = 8;
int treatment[]={
1, 2, 3, 4, 5, 6, 7, 8,
1, 2, 3, 4, 5, 6, 7, 8,
1, 2, 3, 4, 5, 6, 7, 8};
float y[] ={
30.0, 40.0, 38.9, 38.2,
41.8, 52.2, 54.8, 58.2,
20.5, 26.9, 21.4, 25.1,
26.4, 36.7, 28.9, 35.9,
21.0, 25.4, 24.0, 23.3,
34.4, 41.0, 33.0, 34.9};
float bartletts;
float levenes;
float grand_mean;
float cv;
float *treatment_means=NULL;
float *residuals=NULL;
float *studentized_residuals=NULL;
float *std_devs=NULL;
int n_missing = 0;
float *p;
p = imsls_f_homogeneity(n, n_treatment, treatment, y,
IMSLS_BARTLETTS, &bartletts,
IMSLS_LEVENES, &levenes,
IMSLS_LEVENES_MEDIAN,
IMSLS_N_MISSING, &n_missing,
IMSLS_GRAND_MEAN, &grand_mean,
IMSLS_CV, &cv,
IMSLS_TREATMENT_MEANS, &treatment_means,
IMSLS_STD_DEVS, &std_devs,
0);
printf("\n\n\n *** Bartlett\'s Test ***\n\n");
printf("Bartlett\'s p-value = %10.3f\n", p[0]);
printf("Bartlett\'s test statistic = %10.3f\n", bartletts);
printf("\n\n\n *** Levene\'s Test ***\n\n");
printf("Levene\'s p-value = %10.3f\n", p[1]);
printf("Levene\'s test statistic = %10.3f\n", levenes);
imsls_f_write_matrix("Treatment means", n_treatment, 1, treatment_means, 0);
imsls_f_write_matrix("Treatment std devs", n_treatment, 1, std_devs, 0);
printf("\ngrand_mean = %10.3f\n", grand_mean);
printf("cv = %10.3f\n", cv);
printf("n_missing = %d\n", n_missing);
}
Output
*** Bartlett's Test ***
Bartlett's p-value = 0.944
Bartlett's test statistic = 2.257
*** Levene's Test ***
Levene's p-value = 0.994
Levene's test statistic = 0.135
Treatment means
1 23.83
2 30.77
3 28.10
4 28.87
5 34.20
6 43.30
7 38.90
8 43.00
Treatment std devs
1 5.35
2 8.03
3 9.44
4 8.13
5 7.70
6 8.00
7 13.92
8 13.17
grand_mean = 33.871
cv = 28.378
n_missing = 0
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |