Computes the multichannel cross-correlation function of two mutually stationary multichannel time series.
Synopsis
#include <imsls.h>
float
*imsls_f_multi_crosscorrelation (int
n_observations_x,
int n_channel_x, float
x[], int
n_observations_y,
int n_channel_y, float
y[],
int lagmax, ..., 0)
The type double function is imsls_d_multi_crosscorrelation.
Required Arguments
int n_observations_x
(Input)
Number of observations in each channel of the first time series x. n_observations_x must
be greater than or equal to two.
int n_channel_x
(Input)
Number of channels in the first time series x. n_channel_x must be
greater than or equal to one.
float x[]
(Input)
Array of length n_observations_x by
n_channel_x
containing the first time series.
int n_observations_y
(Input)
Number of observations in each channel of the second time series
y. n_observations_y must
be greater than or equal to two.
int n_channel_y
(Input)
Number of channels in the second time series y. n_channel_y must be
greater than or equal to one.
float y[]
(Input)
Array of length n_observations_y by
n_channel_y
containing the second time series.
int lagmax (Input)
Maximum lag of cross-covariances and cross-correlations to be
computed. lagmax must be greater
than or equal to one and less than the minimum of n_observations_x and
n_observations_y.
Return Value
Pointer to an array of length n_channel_x
* n_channel_y
* (2 *
lagmax +
1) containing the cross-correlations between the channels of x
and y.
The mth element of this array contains the cross-correlation between
channel i of the x
series and channel j of the y
series at lag (k-lagmax)
where
i = 1, …, n_channel_x
j = 1, …, n_channel_y
k = 0, 1, …, 2*lagmax,
and
m = (n_channel_x*n_channel_y*k
+(i*n_channel_x+
j))
To release this space, use free. If no solution can be computed, NULL is return.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_multi_crosscorrelation (int
n_observations_x,
int
n_channel_x,
float x[], int
n_observations_y,
int n_channel_y, float
y[],
int lagmax,
IMSLS_RETURN_USER,
float crosscorrelations[],
IMSLS_PRINT_LEVEL,
int iprint,
IMSLS_VARIANCES, float
**x_variance,
float **y_variance,
IMSLS_VARIANCES_USER, float
x_variance[],
float
y_variance[],
IMSLS_CROSS_COVARIANCES, float
**cross_covariances,
IMSLS_CROSS_COVARIANCES_USER,
float
cross_covariances[],
IMSLS_INPUT_MEANS, float
*x_mean_in,
float *y_mean_in,
IMSLS_OUTPUT_MEANS, float
**x_mean_out,
float
**y_mean_out,
IMSLS_OUTPUT_MEANS_USER, float
x_mean_out[],
float
y_mean_out[],
0)
Optional Arguments
IMSLS_RETURN_USER, float
crosscorrelations[] (Output)
If specified, crosscorrelations is a
user-specified array of length n_channel_x * n_channel_y * (2*lagmax + 1)
containing the cross-correlations between the channels of x and y. See
Return Value.
IMSLS_PRINT_LEVEL,
int iprint
(Input)
Printing option. Default = 0.
|
iprint |
Action |
|
0 |
No printing is performed. |
|
1 |
Prints the means and variances. |
|
2 |
Prints the means, variances, and cross-covariances. |
|
3 |
Prints the means, variances, cross-covariances, and cross-correlations. |
IMSLS_VARIANCES,
float
**x_variance,
float
**y_variance
(Output)
If specified, x_variance is the
address of a pointer to an array of length n_channel_x containing
the variances of the channels of x and y_variance is the
address of a pointer to an array of length n_channel_y containing
the variances of the channels of y.
IMSLS_VARIANCES_USER,
float
x_variance[],
float
y_variance[]
(Output)
If specified, x_variance is an array
of length n_channel_x containing
the variances of the channels of x and y_variance is an array
of length n_channel_y containing
the variances of the channels of y. See IMSLS_VARIANCES.
IMSLS_CROSS_COVARIANCES,
float **cross_covariances
(Output)
Address of a pointer to an array of length n_channel_x * n_channel_y * (2*lagmax + 1)
containing the cross-covariances between the channels of x and y. The
mth element of this array contains the cross-covariance between channel
i of the x series and channel
j of the y series at lag
(k-lagmax) where
i = 1, …, n_channel_x
j = 1, …, n_channel_y
k = 0, 1, …, 2*lagmax,
and
m = (n_channel_x*n_channel_y*k
+(i*n_channel_x+
j)).
IMSLS_CROSS_COVARIANCES_USER,
float cross_covariances[]
(Output)
If specified, cross_covariances is
an array of length n_channel_x * n_channel_y * (2*lagmax + 1)
containing the cross-covariances between the channels of x and y. See IMSLS_CROSS_COVARIANCES.
IMSLS_INPUT_MEANS,
float *x_mean_in,
float *y_mean_in
(Input)
If specified, x_mean_in is an array
of length n_channel_x containing
the user input of the estimate of the means of the channels of x and y_mean_in is an array
of length n_channel_y containing
the user input of the estimate of the means of the channels of y.
IMSLS_OUTPUT_MEANS,
float
**x_mean_out,
float **y_mean_out
(Output)
If specified, x_mean_out is the
address of a pointer to an array of length n_channel_x containing
the means of the channels of x and y_mean_out is the
address of a pointer to an array of length n_channel_y containing
the means of the channels of y.
IMSLS_OUTPUT_MEANS_USER,
float
x_mean_out[],
float y_mean_out[]
(Output)
If specified, x_mean_out is an array
of length n_channel_x containing
the means of the channels of x and y_mean_out is an
array of length n_channel_y containing
the means of the channels of y. See IMSLS_OUTPUT_MEANS.
Description
Function imsls_f_multi_crosscorrelation estimates the multichannel cross-correlation function of two mutually stationary multichannel time series. Define the multichannel time series X by
X = (X1, X2, ¼, Xp)
where
Xj = (X1j, X2j, ¼, Xnj)T, j = 1, 2, ¼, p
with n = n_observations_x and p = n_channel_x. Similarly, define the multichannel time series Y by
Y = (Y1, Y2, ¼, Yq)
where
Yj = (Y1j, Y2j, ¼, Ymj)T, j = 1, 2, ¼, q
with m = n_observations_y and q = n_channel_y. The columns of X and Y correspond to individual channels of multichannel time series and may be examined from a univariate perspective. The rows of X and Y correspond to observations of p-variate and q-variate time series, respectively, and may be examined from a multivariate perspective. Note that an alternative characterization of a multivariate time series X considers the columns to be observations of the multivariate time series while the rows contain univariate time series. For example, see Priestley (1981, page 692) and Fuller (1976, page 14).
Let
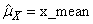
be the row vector containing the means of the channels of X. In particular,
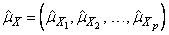
where for j = 1, 2, …, p

Let
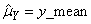
be similarly defined. The cross-covariance of lag k between channel i of X and channel j of Y is estimated by
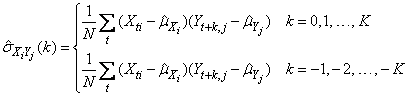
where i = 1, …, p, j = 1, …, q, and K = lagmax. The summation on t extends over all possible cross-products with N equal to the number of cross-products in the sum
Let
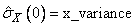
be the row vector consisting of the estimated variances of the channels of X. In particular,
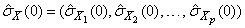
where
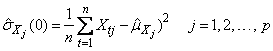
Let
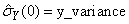
be similarly defined. The cross-correlation of lag k between channel i of X and channel j of Y is estimated by

Example
Consider the Wolfer Sunspot Data
(Y ) (Box and Jenkins 1976, page 530) along with data on northern light
activity (X1) and earthquake
activity (X2) (Robinson 1967, page
204) to be a three-channel time series. Function imsls_f_multi_crosscorrelation
is used to compute the cross-covariances and cross-correlations between
X1 and Y and
between X2 and Y with lags
from
-lagmax
= -10 through lag lagmax
= 10.
#include "imsls.h"
void main () {
int i, lagmax, nobsx, nchanx, nobsy, nchany;
float x[100 * 2], y[100], *result = NULL, *xvar = NULL, *yvar = NULL,
*xmean = NULL, *ymean = NULL, *ccv = NULL;
float data[100][4];
char line[20];
nobsx = nobsy = 100;
nchanx = 2;
nchany = 1;
lagmax = 10;
imsls_f_data_sets (8, IMSLS_X_COL_DIM, 4, IMSLS_RETURN_USER, data, 0);
for (i = 0; i < 100; i++)
{
y[i] = data[i][1];
x[i * 2] = data[i][2];
x[i * 2 + 1] = data[i][3];
}
result =
imsls_f_multi_crosscorrelation (nobsx, nchanx, &x[0], nobsy, nchany,
&y[0], lagmax, IMSLS_VARIANCES, &xvar,
&yvar, IMSLS_OUTPUT_MEANS, &xmean, &ymean,
IMSLS_CROSS_COVARIANCES, &ccv, 0);
imsls_f_write_matrix ("Channel means of x", 1, nchanx, xmean, 0);
imsls_f_write_matrix ("Channel variances of x", 1, nchanx, xvar, 0);
imsls_f_write_matrix ("Channel means of y", 1, nchany, ymean, 0);
imsls_f_write_matrix ("Channel variances of y", 1, nchany, yvar, 0);
printf ("\nMultichannel cross-covariance between x and y\n");
for (i = 0; i < (2 * lagmax + 1); i++)
{
sprintf (line, "Lag K = %d", i - lagmax);
imsls_f_write_matrix (line, nchanx, nchany,
&ccv[nchanx * nchany * i], 0);
}
printf ("\nMultichannel cross-correlation between x and y\n");
for (i = 0; i < (2 * lagmax + 1); i++)
{
sprintf (line, "Lag K = %d", i - lagmax);
imsls_f_write_matrix (line, nchanx, nchany,
&result[nchanx * nchany * i], 0);
}
}
Output
Channel means of x
1 2
63.43 97.97
Channel variances of x
1 2
2644 1978
Channel means of y
46.94
Channel variances of y
1384
Multichannel cross-covariance between x and y
Lag K = -10
1 -20.51
2 70.71
Lag K = -9
1 65.02
2 38.14
Lag K = -8
1 216.6
2 135.6
Lag K = -7
1 246.8
2 100.4
Lag K = -6
1 142.1
2 45.0
Lag K = -5
1 50.70
2 -11.81
Lag K = -4
1 72.68
2 32.69
Lag K = -3
1 217.9
2 -40.1
Lag K = -2
1 355.8
2 -152.6
Lag K = -1
1 579.7
2 -213.0
Lag K = 0
1 821.6
2 -104.8
Lag K = 1
1 810.1
2 55.2
Lag K = 2
1 628.4
2 84.8
Lag K = 3
1 438.3
2 76.0
Lag K = 4
1 238.8
2 200.4
Lag K = 5
1 143.6
2 283.0
Lag K = 6
1 253.0
2 234.4
Lag K = 7
1 479.5
2 223.0
Lag K = 8
1 724.9
2 124.5
Lag K = 9
1 925.0
2 -79.5
Lag K = 10
1 922.8
2 -279.3
Multichannel cross-correlation between x and y
Lag K = -10
1 -0.01072
2 0.04274
Lag K = -9
1 0.03400
2 0.02305
Lag K = -8
1 0.1133
2 0.0819
Lag K = -7
1 0.1290
2 0.0607
Lag K = -6
1 0.07431
2 0.02718
Lag K = -5
1 0.02651
2 -0.00714
Lag K = -4
1 0.03800
2 0.01976
Lag K = -3
1 0.1139
2 -0.0242
Lag K = -2
1 0.1860
2 -0.0923
Lag K = -1
1 0.3031
2 -0.1287
Lag K = 0
1 0.4296
2 -0.0633
Lag K = 1
1 0.4236
2 0.0333
Lag K = 2
1 0.3285
2 0.0512
Lag K = 3
1 0.2291
2 0.0459
Lag K = 4
1 0.1248
2 0.1211
Lag K = 5
1 0.0751
2 0.1710
Lag K = 6
1 0.1323
2 0.1417
Lag K = 7
1 0.2507
2 0.1348
Lag K = 8
1 0.3790
2 0.0752
Lag K = 9
1 0.4836
2 -0.0481
Lag K = 10
1 0.4825
2 -0.1688
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |