Evaluates the noncentral chi-squared distribution function.

Synopsis

#include <imsls.h>

float imsls_f_non_central_chi_sq (float chi_squared, float df , float delta)

The type double function is imsls_d_non_central_chi_sq.

Required Arguments

float chi_squared   (Input)
Argument for which the noncentral chi-squared distribution function is to be evaluated.

float df   (Input)
Number of degrees of freedom of the noncentral chi-squared distribution. Argument df must be greater than or equal to 0.5

float delta (Input)
The noncentrality parameter.  delta must be nonnegative, and   delta + df must be less than or equal to 200,000.

Return Value

The probability that a noncentral chi-squared random variable takes a value less than or equal to chi_squared.

Description

Function imsls_f_non_central_chi_sq evaluates the distribution function of a noncentral chi-squared random variable with df degrees of freedom and noncentrality parameter alam, that is, with v = df, l = alam, and x = chi_squared,

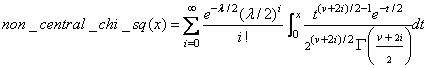
where G(×) is the gamma function. This is a series of central chi-squared distribution functions with Poisson weights. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.

The noncentral chi-squared random variable can be defined by the distribution function above, or alternatively and equivalently, as the sum of squares of independent normal random variables. If Yi have independent normal distributions with means mi and variances equal to one and

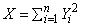
then X has a noncentral chi-squared distribution with n degrees of freedom and noncentrality parameter equal to

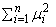
With a noncentrality parameter of zero, the noncentral chi-squared distribution is the same as the chi-squared distribution.

Function imsls_f_non_central_chi_sq determines the point at which the Poisson weight is greatest, and then sums forward and backward from that point, terminating when the additional terms are sufficiently small or when a maximum of 1000 terms have been accumulated. The recurrence relation 26.4.8 of Abramowitz and Stegun (1964) is used to speed the evaluation of the central chi-squared distribution functions.

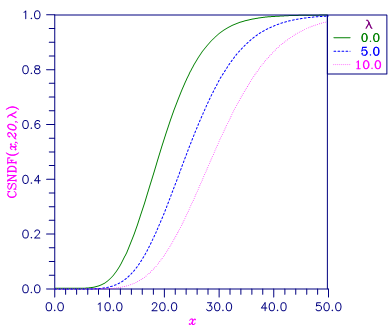
Figure 11-3   Noncentral Chi-squared Distribution Function

Example

In this example, imsls_f_non_central_chi_sq is used to compute the probability that a random variable that follows the noncentral chi-squared distribution with noncentrality parameter of 1 and with 2 degrees of freedom is less than or equal to 8.642.

#include <imsls.h>

#include <stdio.h>

void main()

{

        float chsq = 8.642;

        float df = 2.0;

        float alam = 1.0;

        float p;

        p = imsls_f_non_central_chi_sq(chsq, df, alam);

        printf("The probability that a noncentral chi-squared random\n"

        "variable with %2.0f df and noncentrality parameter %3.1f is less\n"

        "than %5.3f is %5.3f.\n", df, alam, chsq, p);

}

Output

The probability that a noncentral chi-squared random

variable with 2 df and noncentrality parameter 1.0 is less

than 8.642 is 0.950

 

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260