Performs a test for normality.
Synopsis
#include <imsls.h>
float imsls_f_normality_test (int n_observations, float x[], ..., 0)
The type double function is imsls_d_normality_test.
Required Arguments
int
n_observations (Input)
Number of observations. Argument
n_observations
must be in the range from 3 to 2,000, inclusive, for the Shapiro-Wilk W
test and must be greater than 4 for the Lilliefors test.
float x[]
(Input)
Array of size n_observations
containing the observations.
Return Value
The p-value for the Shapiro-Wilk W test or the Lilliefors test for normality. The Shapiro-Wilk test is the default. If the Lilliefors test is used, probabilities less than 0.01 are reported as 0.01, and probabilities greater than 0.10 for the normal distribution are reported as 0.5. Otherwise, an approximate probability is computed.
Synopsis with Optional Arguments
#include <imsls.h>
float
imsls_f_normality_test (int
n_observations, float
x[],
IMSLS_SHAPIRO_WILK_W, float
*shapiro_wilk_w,
IMSLS_LILLIEFORS, float
*max_difference,
IMSLS_CHI_SQUARED, int
n_categories, float
*df,
float *chi_squared,
0)
Optional Arguments
IMSLS_SHAPIRO_WILK_W, float
*shapiro_wilk_w (Output)
Indicates the Shapiro-Wilk
W test is to be performed. The Shapiro-Wilk W statistic is
returned in shapiro_wilk_w.
Argument IMSLS_SHAPIRO_WILK_W
is the default test.
IMSLS_LILLIEFORS, float
*max_difference (Output)
Indicates the Lilliefors test is
to be performed. The maximum absolute difference between the empirical and the
theoretical distributions is returned in max_difference.
IMSLS_CHI_SQUARED, int
n_categories (Input),
float *df, float
*chi_squared (Output)
Indicates the chi-squared
goodness-of-fit test is to be performed. Argument n_categories is
the number of cells into which the observations are to be tallied. The degrees
of freedom for the test are returned in argument df, and the chi-square
statistic is returned in argument chi_squared.
Description
Three methods are provided for testing normality: the Shapiro-Wilk W test, the Lilliefors test, and the chi-squared test.
Shapiro-Wilk W Test
The Shapiro-Wilk W test is thought by D’Agostino and Stevens (1986, p. 406) to be one of the best omnibus tests of normality. The function is based on the approximations and code given by Royston (1982a, b, c). It can be used in samples as large as 2,000 or as small as 3. In the Shapiro and Wilk test, W is given by
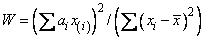
where x(i) is the i-th largest order statistic and x is the sample mean. Royston (1982) gives approximations and tabled values that can be used to compute the coefficients ai, i = 1, …, n, and obtains the significance level of the W statistic.
Lilliefors Test
This function computes Lilliefors test and its
p-values for a normal distribution in which both the mean and variance
are estimated. The one-sample, two-sided Kolmogorov-Smirnov statistic
D is first computed. The p-values are then computed using an
analytic approximation given by Dallal and Wilkinson (1986). Because Dallal and
Wilkinson give approximations in the range
(0.01, 0.10) if the computed probability of a
greater D is less than 0.01, an IMSLS_NOTE
is issued and the p-value is set to 0.50. Note that because parameters
are estimated, p-values in Lilliefors test are not the same as in the
Kolmogorov-Smirnov Test.
Observations should not be tied. If tied observations are found, an informational message is printed. A general reference for the Lilliefors test is Conover (1980). The original reference for the test for normality is Lilliefors (1967).
Chi-Squared Test
This function computes the chi-squared statistic, its p-value, and the degrees of freedom of the test. Argument n_categories finds the number of intervals into which the observations are to be divided. The intervals are equiprobable except for the first and last interval which are infinite in length.
If more flexibility is desired for the specification of intervals, the same test can be performed with a call to function imsls_f_chi_squared_test using the optional arguments described for that function.
Examples
Example 1
The following example is taken from Conover (1980, pp. 195, 364). The data consists of 50 two-digit numbers taken from a telephone book. The W test fails to reject the null hypothesis of normality at the .05 level of significance.
#include <imsls.h>
void main()
{
int n_observations = 50;
float x[] = {23.0, 36.0, 54.0, 61.0, 73.0, 23.0,
37.0, 54.0, 61.0, 73.0, 24.0, 40.0,
56.0, 62.0, 74.0, 27.0, 42.0, 57.0,
63.0, 75.0, 29.0, 43.0, 57.0, 64.0,
77.0, 31.0, 43.0, 58.0, 65.0, 81.0,
32.0, 44.0, 58.0, 66.0, 87.0, 33.0,
45.0, 58.0, 68.0, 89.0, 33.0, 48.0,
58.0, 68.0, 93.0, 35.0, 48.0, 59.0,
70.0, 97.0};
float p_value;
/* Shapiro-Wilk test */
p_value = imsls_f_normality_test (n_observations, x,
0);
printf ("p-value = %11.4f.\n", p_value);
}
Output
p-value = 0.2309
Example 2
The following example uses the same data as the previous example. Here, the Shapiro-Wilk W statistic is output.
#include <imsls.h>
void main()
{
int n_observations = 50;
float x[] = {23.0, 36.0, 54.0, 61.0, 73.0, 23.0,
37.0, 54.0, 61.0, 73.0, 24.0, 40.0,
56.0, 62.0, 74.0, 27.0, 42.0, 57.0,
63.0, 75.0, 29.0, 43.0, 57.0, 64.0,
77.0, 31.0, 43.0, 58.0, 65.0, 81.0,
32.0, 44.0, 58.0, 66.0, 87.0, 33.0,
45.0, 58.0, 68.0, 89.0, 33.0, 48.0,
58.0, 68.0, 93.0, 35.0, 48.0, 59.0,
70.0, 97.0};
float p_value, shapiro_wilk_w;
/* Shapiro-Wilk test */
p_value = imsls_f_normality_test (n_observations, x,
IMSLS_SHAPIRO_WILK_W,
&shapiro_wilk_w,
0);
printf ("p-value = %11.4f.\n", p_value);
printf ("Shapiro Wilk W statistic = %11.4f.\n",
shapiro_wilk_w);
}
Output
p-value = 0.2309.
Shapiro Wilk W statistic = 0.9642
Warning Errors
IMSLS_ALL_OBS_TIED All observations in “x” are tied.
Fatal Errors
IMSLS_NEED_AT_LEAST_5 All but # elements of “x” are missing. At least five nonmissing observations are necessary to continue.
IMSLS_NEG_IN_EXPONENTIAL In testing the exponential distribution, an invalid element in “x” is found (“x[]” = #). Negative values are not possible in exponential distributions.
IMSLS_NO_VARIATION_INPUT There is no variation in the input data. All nonmissing observations are tied.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |