Evaluates the Poisson distribution function.

Synopsis

#include <imsls.h>

float imsls_f_poisson_cdf (int k, float theta)

The type double function is imsls_d_poisson_cdf.

Required Arguments

int k   (Input)
Argument for which the Poisson distribution function is to be evaluated.

float theta   (Input)
Mean of the Poisson distribution. Argument theta must be positive.

Return Value

The probability that a Poisson random variable takes a value less than or equal
to k.

Description

Function imsls_f_poisson_cdf evaluates the distribution function of a Poisson random variable with parameter theta. The mean of the Poisson random variable, theta, must be positive. The probability function (with θ = theta) is as follows:

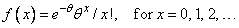
The individual terms are calculated from the tails of the distribution to the mode of the distribution and summed. Function imsls_f_poisson_cdf uses the recursive relationship

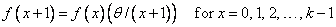
with f (0) = e−q.

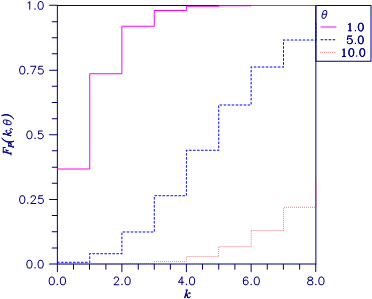
Figure 11-1   Plot of Fp (k, θ)

Example

Suppose X is a Poisson random variable with θ = 10. In this example, we evaluate the probability that X is less than or equal to 7.

#include <imsls.h>

void main()
{
    int         k = 7;
    float       theta = 10.0;
    float       p;

    p = imsls_f_poisson_cdf(k, theta);
    printf("Pr(x <= 7) = %6.4f\n", p);
}

Output

Pr(x <= 7) = 0.2202

Informational Errors

IMSLS_LESS_THAN_ZERO                         Since “k” = # is less than zero, the distribution function is set to zero.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260