Performs a polynomial least-squares regression.
Synopsis
#include <imsls.h>
float *imsls_f_poly_regression (int n_observations, float x[], float y[], int degree, ..., 0)
The type double function is imsls_d_poly_regression.
Required Arguments
int
n_observations (Input)
Number of
observations.
float x[]
(Input)
Array of length n_observations
containing the independent variable.
float y[]
(Input)
Array of length n_observations
containing the dependent variable.
int degree
(Input)
Degree of the polynomial.
Return Value
A pointer to the array of size degree + 1 containing the coefficients of the fitted polynomial. If a fit cannot be computed, NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_poly_regression (int
n_observations, float
x[],
float
y[],
int
degree,
IMSLS_WEIGHTS, float
weights[],
IMSLS_SSQ_POLY, float
**ssq_poly,
IMSLS_SSQ_POLY_USER, float
ssq_poly[],
IMSLS_SSQ_POLY_COL_DIM, int
ssq_poly_col_dim,
IMSLS_SSQ_LOF, float
**ssq_lof,
IMSLS_SSQ_LOF_USER, float
ssq_lof[],
IMSLS_SSQ_LOF_COL_DIM, int
ssq_lof_col_dim,
IMSLS_X_MEAN, float
*x_mean,
IMSLS_X_VARIANCE, float
*x_variance,
IMSLS_ANOVA_TABLE, float
**anova_table,
IMSLS_ANOVA_TABLE_USER, float
anova_table[],
IMSLS_DF_PURE_ERROR, int
*df_pure_error,
IMSLS_SSQ_PURE_ERROR, float
*ssq_pure_error,
IMSLS_RESIDUAL, float
**residual,
IMSLS_RESIDUAL_USER, float
residual[],
IMSLS_POLY_REGRESSION_INFO, Imsls_f_poly_regression **poly_info,
IMSLS_RETURN_USER, float
coefficients[],
0)
Optional Arguments
IMSLS_WEIGHTS, float weights[]
(Input)
Array with n_observations
components containing the array of weights for the observation.
Default:
weights[] = 1
IMSLS_SSQ_POLY, float
**ssq_poly (Output)
Address of a pointer to the internally
allocated array containing the sequential sums of squares and other statistics.
Row i corresponds to
xi, i = 0, ..., degree − 1, and the columns are
described as follows:
|
Column |
Description |
|
0 |
degrees of freedom |
|
1 |
sums of squares |
|
2 |
F-statistic |
|
3 |
p-value |
IMSLS_SSQ_POLY_USER, float
ssq_poly[] (Output)
Storage for array ssq_poly is provided
by the user. See IMSLS_SSQ_POLY.
IMSLS_SSQ_POLY_COL_DIM, int
ssq_poly_col_dim (Input)
Column dimension of ssq_poly.
Default:
ssq_poly_col_dim = 4
IMSLS_SSQ_LOF, float **ssq_lof
(Output)
Address of a pointer to the internally allocated array containing
the lack-of-fit statistics. Row i corresponds to xi, i = 0, ..., degree − 1, and the columns are
described in the following table:
|
Column |
Description |
|
0 |
degrees of freedom |
|
1 |
lack-of-fit sums of squares |
|
2 |
F-statistic for testing lack-of-fit for a polynomial model of degree i |
|
3 |
p-value for the test |
IMSLS_SSQ_LOF_USER, float ssq_lof[]
(Output)
Storage for array ssq_lof is provided by
the user. See IMSLS_SSQ_LOF.
IMSLS_SSQ_LOF_COL_DIM, int
ssq_lof_col_dim (Input)
Column dimension of ssq_lof.
Default:
ssq_lof_col_dim = 4
IMSLS_X_MEAN, float *x_mean
(Output)
Mean of x.
IMSLS_X_VARIANCE, float
*x_variance (Output)
Variance of x.
IMSLS_ANOVA_TABLE, float
**anova_table (Output)
Address of a pointer to the array
containing the analysis of variance table.
|
Column |
Description |
|
0 |
degrees of freedom for the model |
|
1 |
degrees of freedom for error |
|
2 |
total (corrected) degrees of freedom |
|
3 |
sum of squares for the model |
|
4 |
sum of squares for error |
|
5 |
total (corrected) sum of squares |
|
6 |
model mean square |
|
7 |
error mean square |
|
8 |
overall F-statistic |
|
9 |
p-value |
|
10 |
R2 (in percent) |
|
11 |
adjusted R2 (in percent) |
|
12 |
estimate of the standard deviation |
|
13 |
overall mean of y |
|
14 |
coefficient of variation (in percent) |
IMSLS_ANOVA_TABLE_USER, float
anova_table[] (Output)
Storage for anova_table is
provided by the user. See IMSLS_ANOVA_TABLE.
IMSLS_DF_PURE_ERROR, int
*df_pure_error (Output)
If specified, the degrees of
freedom for pure error are returned in df_pure_error.
IMSLS_SSQ_PURE_ERROR, float
*ssq_pure_error (Output)
If specified, the sums of squares
for pure error are returned in ssq_pure_error.
IMSLS_RESIDUAL, float
**residual (Output)
Address of a pointer to the array
containing the residuals.
IMSLS_RESIDUAL_USER, float
residual[] (Output)
Storage for array residual is provided
by the user. See IMSLS_RESIDUAL.
IMSLS_POLY_REGRESSION_INFO,
Imsls_f_poly_regression
**poly_info (Output)
Address of a pointer to an internally
allocated structure containing the information about the polynomial fit required
as input for IMSL function imsls_f_poly_prediction.
IMSLS_RETURN_USER, float
coefficients[] (Output)
If specified, the least-squares
solution for the regression coefficients is stored in array coefficients of size
degree + 1
provided by the user.
Description
Function imsls_f_poly_regression computes estimates of the regression coefficients in a polynomial (curvilinear) regression model. In addition to the computation of the fit, imsls_f_poly_regression computes some summary statistics. Sequential sums of squares attributable to each power of the independent variable (stored in ssq_poly) are computed. These are useful in assessing the importance of the higher order powers in the fit. Draper and Smith (1981, pp. 101−102) and Neter and Wasserman (1974, pp. 278−287) discuss the interpretation of the sequential sums of squares. The statistic R2 is the percentage of the sum of squares of y about its mean explained by the polynomial curve. Specifically,
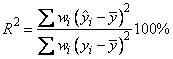
where
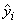
is the fitted y value at xi and
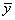 is the mean of
y. This statistic is useful in assessing the overall fit of the curve to
the data. R2 must be between 0 and
100 percent, inclusive. R2 = 100 percent
indicates a perfect fit to the data.
is the mean of
y. This statistic is useful in assessing the overall fit of the curve to
the data. R2 must be between 0 and
100 percent, inclusive. R2 = 100 percent
indicates a perfect fit to the data.
Estimates of the regression coefficients in a polynomial model are computed using orthogonal polynomials as the regressor variables. This reparameterization of the polynomial model in terms of orthogonal polynomials has the advantage that the loss of accuracy resulting from forming powers of the x-values is avoided. All results are returned to the user for the original model (power form).
Function imsls_f_poly_regression is based on the algorithm of Forsythe (1957). A modification to Forsythe’s algorithm suggested by Shampine (1975) is used for computing the polynomial coefficients. A discussion of Forsythe’s algorithm and Shampine’s modification appears in Kennedy and Gentle (1980, pp. 342−347).
Examples
Example 1
A polynomial model is fitted to data discussed by
Neter and Wasserman
(1974, pp. 279−285). The data set contains
the response variable y measuring coffee sales (in hundred gallons) and
the number of self-service coffee dispensers. Responses for 14 similar
cafeterias are in the data set. A graph of the results is also given.
#include <imsls.h>
#define
DEGREE 2
#define
NOBS
14
main()
{
float *coefficients;
float x[] = {0.0, 0.0, 1.0, 1.0, 2.0, 2.0,
4.0,
4.0, 5.0, 5.0, 6.0, 6.0, 7.0, 7.0};
float y[] = {508.1, 498.4, 568.2, 577.3,
651.7, 657.0,
755.3,
758.9, 787.6, 792.1, 841.4, 831.8, 854.7, 871.4};
coefficients = imsls_f_poly_regression (NOBS, x, y, DEGREE,
0);
imsls_f_write_matrix("Least-Squares Polynomial
Coefficients",
DEGREE + 1, 1, coefficients,
IMSLS_ROW_NUMBER_ZERO,
0);
}
Output
Least-Squares Polynomial
Coefficients
0
503.3
1
78.9
2 -4.0
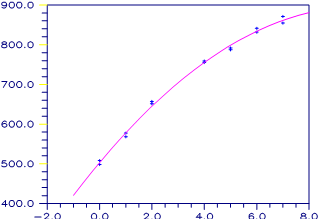
Figure 2-1 A Polynomial Fit
Example 2
This example is a continuation of the initial example. Here, many optional arguments are used.
#include <stdio.h>
#include
<imsls.h>
#define
DEGREE 2
#define
NOBS
14
void main()
{
int iset = 1,
dfpe;
float
*coefficients, *anova_table, sspe, *ssqpoly, *ssqlof;
float x[] = {0.0, 0.0, 1.0, 1.0, 2.0, 2.0,
4.0,
4.0, 5.0, 5.0, 6.0, 6.0, 7.0, 7.0};
float y[] = {508.1, 498.4, 568.2, 577.3,
651.7, 657.0,
755.3,
758.9, 787.6, 792.1, 841.4, 831.8, 854.7, 871.4};
char
*coef_rlab[2];
char *coef_clab[] = {" ", "intercept",
"linear",
"quadratic"};
char *stat_clab[] = {" ", "Degrees
of\nFreedom",
"Sum of\nSquares",
"\nF-Statistic",
"\np-value"};
char *anova_rlab[] =
{
"degrees of freedom for regression",
"degrees of freedom for error",
"total (corrected) degrees of
freedom",
"sum of squares for
regression",
"sum of squares for error",
"total (corrected) sum of
squares",
"regression mean square",
"error mean square",
"F-statistic",
"p-value",
"R-squared (in percent)",
"adjusted R-squared (in
percent)",
"est. standard deviation of model error",
"overall mean of y",
"coefficient of variation (in percent)"};
coefficients = imsls_f_poly_regression(NOBS, x, y,
DEGREE,
IMSLS_SSQ_POLY,
&ssqpoly,
IMSLS_SSQ_LOF,
&ssqlof,
IMSLS_ANOVA_TABLE,
&anova_table,
IMSLS_DF_PURE_ERROR,
&dfpe,
IMSLS_SSQ_PURE_ERROR,
&sspe,
0);
imsls_write_options(-1,
&iset);
imsls_f_write_matrix("Least Squares Polynomial
Coefficients",
1, DEGREE + 1,
coefficients,
IMSLS_COL_LABELS,
coef_clab,
0);
coef_rlab[0] = coef_clab[2];
coef_rlab[1] = coef_clab[3];
imsls_f_write_matrix("Sequential Statistics", DEGREE, 4, ssqpoly,
IMSLS_COL_LABELS,
stat_clab,
IMSLS_ROW_LABELS,
coef_rlab,
IMSLS_WRITE_FORMAT,
"%3.1f%8.1f%6.1f%6.4f",
0);
imsls_f_write_matrix("Lack-of-Fit Statistics", DEGREE,
4,
ssqlof,
IMSLS_COL_LABELS,
stat_clab,
IMSLS_ROW_LABELS, coef_rlab,
IMSLS_WRITE_FORMAT,
"%3.1f%8.1f%6.1f%6.4f",
0);
imsls_f_write_matrix("* * * Analysis of Variance * *
*\n", 15,
1,
anova_table,
IMSLS_ROW_LABELS,
anova_rlab,
IMSLS_WRITE_FORMAT,
"%9.2f",
0);
}
Output
Least Squares Polynomial
Coefficients
intercept linear
quadratic
503.3
78.9
-4.0
Sequential
Statistics
Degrees of Sum
of
Freedom Squares F-Statistic
p-value
linear
1.0 220644.2
3415.8
0.0000
quadratic 1.0
4387.7 67.9
0.0000
Lack-of-Fit
Statistics
Degrees of Sum
of
Freedom Squares F-Statistic
p-value
linear
5.0 4793.7
22.0
0.0004
quadratic
4.0
405.9 2.3
0.1548
* * * Analysis of Variance * *
*
degrees of freedom for
regression
2.00
degrees of freedom for
error
11.00
total (corrected) degrees of freedom
13.00
sum of squares for
regression
225031.94
sum of squares for
error
710.55
total (corrected) sum of squares
225742.48
regression mean
square
112515.97
error mean
square
64.60
F-statistic
1741.86
p-value
0.00
R-squared (in
percent)
99.69
adjusted R-squared (in
percent)
99.63
est. standard deviation of model error
8.04
overall mean of
y
710.99
coefficient of variation (in percent)
1.13
Warning Errors
IMSLS_CONSTANT_YVALUES The y values are constant. A zero-order polynomial is fit. High order coefficients are set to zero.
IMSLS_FEW_DISTINCT_XVALUES There are too few distinct x values to fit the desired degree polynomial. High order coefficients are set to zero.
IMSLS_PERFECT_FIT A perfect fit was obtained with a polynomial of degree less than degree. High order coefficients are set to zero.
Fatal Errors
IMSLS_NONNEG_WEIGHT_REQUEST_2 All weights must be nonnegative.
IMSLS_ALL_OBSERVATIONS_MISSING Each (x, y) point contains NaN. There are no valid data.
IMSLS_CONSTANT_XVALUES The x values are constant.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |