Performs a test for randomness.
Synopsis
#include <imsls.h>
float
imsls_f_randomness_test (int
n_observations, float x[],
int n_run..., 0)
The type double function is imsls_d_randomness_test.
Required Arguments
int
n_observations (Input)
Number of observations in x.
float x[]
(Input)
Array of size n_observations
containing the data.
int n_run
(Input)
Length of longest run for which tabulation is desired. For
optional arguments IMSLS_PAIRS, IMSLS_DSQUARE, and
IMSLS_DCUBE,
n_run stands for
the number of equiprobable cells into which the statistics are to be
tabulated.
Return Value
The probability of a larger chi-squared statistic for testing the null hypothesis of a uniform distribution.
Synopsis with Optional Arguments
#include <imsls.h>
float imsls_f_randomness_test (int n_observations_x, float x[], int n_run, ...
IMSLS_RUNS, float **runs_count, float **covariances,
IMSLS_RUNS_USER, float
runs_count[], float covariances[],
IMSLS_PAIRS, int
pairs_lag,
float **pairs_count,
IMSLS_PAIRS_USER, int pairs_lag, float pairs_count[],
IMSLS_DSQUARE, float **dsquare_count,
IMSLS_DSQUARE_USER, float dsquare_count[],
IMSLS_DCUBE, float **dcube_count,
IMSLS_DCUBE_USER, float dcube_count[],
IMSLS_RUNS_EXPECT, float **runs_expect,
IMSLS_RUNS_EXPECT_USER, float runs_expect[],
IMSLS_EXPECT, float *expect,
IMSLS_CHI_SQUARED, float *chi_squared,
IMSLS_DF, float *df,
IMSLS_RETURN USER, float *pvalue,
0)
Optional Arguments
IMSLS_RUNS, float **runs_count, float **covariances, (Output) or
IMSLS_PAIRS, int pairs_lag (Input), float **pairs_count,(Output) or
IMSLS_DSQUARE, float **dsquare_count, (Output) or
IMSLS_DCUBE, float **dcube_count, (Output)
IMSLS_RUNS indicates the runs test is to be performed. Array of length n_run containing the counts of the number of runs up of each length is returned in *runs_counts. n_run by n_observations matrix containing the variances and covariances of the counts is returned in *covariances. IMSLS_RUNS is the default test, however, to return the counts and covariances IMSLS_RUNS argument must be used.
IMSLS_PAIRS indicates the pairs test is to be performed. The lag to be used in computing the pairs statistic is stored in pairs_lag. Pairs (X[i], X[i + pairs_lag]) for i = 0,…, N – pairs_lag -1 are tabulated, where N is the total sample size. n_run by n_run matrix containing the count of the number of pairs in each cell is returned in pairs_user.
IMSLS_DSQUARE indicates the d2 test is to be performed. **dsquare_counts is an address of a pointer to an internally allocated array of length n_run containing the tabulations for the d2 test.
IMSLS_DCUBE indicates the triplets test is to be performed. **dcube_counts is an address of a pointer to an internally allocated array of length n_run by n_run by n_run containing the tabulations for the triplets test.
IMSLS_RUNS_USER, float
runs_counts[],
float
covariances[]
(Output)
Storage for runs_counts and
covariances
is provided by the user. See IMSLS_RUNS.
IMSLS_PAIRS_USER, int
pairs_lag,
float
pairs_counts[]
(Output)
Storage for pairs_lag and
pairs_counts is provided by the
user. See IMSLS_PAIRS.
IMSLS_DSQUARE_USER, float dsquare_count[] (Output)
Storage for
dsquare_count is provided by the
user.
See IMSLS_DSQUARE.
IMSLS_DCUBE_USER, float dcube_count[] (Output)
Storage for
dcube_count
is provided by the user. See IMSLS_DCUBE.
IMSLS_CHI_SQUARED, float *chi_squared (Output)
Chi-squared
statistic for testing the null hypothesis of a uniform distribution.
IMSLS_DF, float *df (Output)
Degrees of
freedom for chi-squared.
IMSLS_RETURN_USER, float *pvalue
(Output)
If specified,
pvalue returns the
probability of a larger chi-squared statistic for testing the null hypothesis of
a uniform distribution.
If IMSLS_RUNS is specified:
IMSLS_RUNS_EXPECT, float **runs_expect
(Output)
The address of a pointer
to an internally allocated array of length
n_run containing the expected
number of runs of each length.
IMSLS_RUNS_EXPECT_USER, float runs_expect[]
(Output)
Storage for
runs_expect
is provided by the user.
See IMSLS_RUNS_EXPECT.
If IMSLS_PAIRS, IMSLS_DSQUARE, or IMSLS_DCUBE is specified:
IMSLS_EXPECT, float **expect
(Output)
Expected
number of counts for each cell. This argument is optional only if one of
IMSLS_PAIRS,
IMSLS_DSQUARE, or
IMSLS_DCUBE
is used.
Description
Runs Up Test
Function imsls_f_randomness_test performs one of four different tests for randomness. Optional argument IMSLS_RUNS computes statistics for the runs up test. Runs tests are used to test for cyclical trend in sequences of random numbers. If the runs down test is desired, each observation should first be multiplied by -1 to change its sign, and IMSLS_RUNS called with the modified vector of observations.
IMSLS_RUNS first tallies the number of runs up (increasing sequences) of each desired length. For i = 1, K, r - 1, where r = n_run, runs_count[i] contains the number of runs of length i. runs_count[n_run] contains the number of runs of length n_run or greater. As an example of how runs are counted, the sequence (1, 2, 3, 1) contains 1 run up of length 3, and one run up of length 1.
After tallying the number of runs up of each length, IMSLS_RUNS
computes the
expected values and the covariances of the counts according to
methods given by Knuth (1981, pages 65-67). Let R denote a vector of
length
n_run containing
the number of runs of each length so that the
i-th element of R, ri, contains the count of
the runs of length i. Let SR denote the covariance
matrix of R under the null hypothesis of randomness, and let mR denote the vector of
expected values for R under this null hypothesis, then an approximate
chi-squared statistic with n_run
degrees of freedom is given as
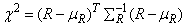
In general, the larger the value of each element of mR, the better the chi-squared approximation.
Pairs Test
IMSLS_PAIRS
computes the pairs test (or the Good’s serial test) on a hypothesized sequence
of uniform (0,1) pseudorandom numbers. The test proceeds as follows. Subsequent
pairs (X(i),
X(i
+ pairs_lag))
are tallied into a k ´ k
matrix, where
k = n_run.
In this tally, element (j, m) of the matrix is incremented,
where
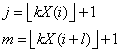
where l = pairs_lag,
and the notation ë û represents the greatest integer function,
ëYû is the greatest integer less than or equal
to Y, where Y is a real number. If l = 1, then
i
= 1, 3, 5, K, n - 1. If l > 1, then i = 1,
2, 3, ¼,
n - l, where n is
the total number of pseudorandom numbers input on the current invocation of
IMSLS_pAIRS
(i.e., n = n_observations).
Given the tally matrix in pairs_count, chi-squared is computed as
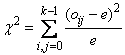
where e = åoij/k2, and oij is the observed count in cell (i, j) (oij = pairs_count(i, j)).
Because pair statistics for the trailing observations are not tallied on any call, the user should call IMSLS_PAIRS with n_observations as large as possible. For pairs_lag < 20 and n_observations = 2000, little power is lost.
d 2 Test
IMSLS_DSQAR computes the d2 test for succeeding quadruples of hypothesized pseudorandom uniform (0, 1) deviates. The d2 test is performed as follows. Let X, X2, X3, and X4 denote four pseudorandom uniform deviates, and consider
D2 = (X3 -X1)2 + (X4 - X2)2
The probability distribution of D2 is given as
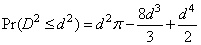
when D2 ≤ 1, where p denotes the value of pi. If D2 > 1, this probability is given as
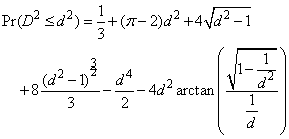
See Gruenberger and Mark (1951) for a derivation of this distribution.
For each succeeding set of 4 pseudorandom uniform numbers input in X, d2 and the cumulative probability of d2 (Pr(D2 £ d2)) are computed. The resulting probability is tallied into one of k = n_run equally spaced intervals.
Let n denote the number of sets of four random
numbers input (n = the total number of observations/4). Then, under the
null hypothesis that the numbers input are random uniform (0, 1) numbers, the
expected value for each element in dsquare_count
is
e = n/k. An approximate chi-squared statistic is
computed as
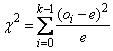
where oi = dsquare_count(i) is the observed count. Thus, c2 has k - 1 degrees of freedom, and the null hypothesis of pseudorandom uniform (0, 1) deviates is rejected if c2 is too large. As n increases, the chi-squared approximation becomes better. A useful generalization is that e > 5 yields a good chi-squared approximation.
Triplets Test
IMSLS_DCUBE
computes the triplets test on a sequence of hypothesized pseudorandom uniform(0,
1) deviates. The triplets test is computed as follows:
Each set of three
successive deviates, X1, X2, and X3, is tallied into one
of m3 equal sized cubes,
where m = n_run.
Let i = [mX1] + 1, j =
[mX2] + 1, and
k = [mX3] + 1. For the
triplet (X1, X2, X3), dcube_count(i,
j, k) is incremented.
Under the null hypothesis of pseudorandom uniform(0, 1) deviates, the m3 cells are equally probable and each has expected value e = n/m3, where n is the number of triplets tallied. An approximate chi-squared statistic is computed as
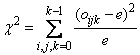
where oijk = dcube_count(i, j, k).
The computed chi-squared has m3 - 1 degrees of freedom, and the null hypothesis of pseudorandom uniform (0, 1) deviates is rejected if c2 is too large.
Examples
Example 1
The following example illustrates the use of the runs test on 104 pseudo-random uniform deviates. In the example, 2000 deviates are generated for each call to IMSLS_RUNS. Since the probability of a larger chi-squared statistic is 0.1872, there is no strong evidence to support rejection of this null hypothesis of randomness.
#include <imsls.h>
#include <stdio.h>
void main()
{
int nran = 10000, n_run = 6;
char *fmt = "%8.1f";
float *x, pvalue, *runs_counts, *runs_expect, chisq, df;
imsls_random_seed_set(123457);
x = imsls_f_random_uniform(nran, 0);
pvalue = imsls_f_randomness_test(nran, x, n_run,
IMSLS_CHI_SQUARED, &chisq,
IMSLS_DF, &df,
IMSLS_RUNS_EXPECT, &runs_expect,
IMSLS_RUNS, &runs_counts, &covariances,
0);
imsls_f_write_matrix("runs_counts", 1, n_run, runs_counts, 0);
imsls_f_write_matrix("runs_expect", 1, n_run, runs_expect,
IMSLS_WRITE_FORMAT, fmt,
0);
imsls_f_write_matrix("covariances", n_run, n_run, covariances,
IMSLS_WRITE_FORMAT, fmt,
0);
printf("chisq = %f\n", chisq);
printf("df = %f\n", df);
printf("pvalue = %f\n", pvalue);
}
Output
runs_count
1
2
3
4
5 6
1709.0
2046.0 953.0 260.0
55.0
4.0
runs_expect
1
2
3
4
5 6
1667.3
2083.4 916.5 263.8
57.5
11.9
covariances
1
2
3
4
5 6
1
1278.2 -194.6 -148.9
-71.6 -22.9 -6.7
2
-194.6 1410.1 -490.6
-197.2 -55.2 -14.4
3
-148.9 -490.6 601.4
-117.4 -31.2
-7.8
4 -71.6 -197.2
-117.4 222.1 -10.8
-2.6
5 -22.9 -55.2
-31.2 -10.8
54.8 -0.6
6
-6.7 -14.4
-7.8 -2.6
-0.6 11.7
chisq =
8.76514
df =
6.00000
pvalue = 0.187225
Example 2
The following example illustrates the calculations of the IMSLS_pAIRS statistics when a random sample of size 104 is used and the pairs_lag is 1. The results are not significant. IMSL routine imsls_f_random_uniform (Chapter 12, “Random Number Generation.p<.STCH18.DOC!RNUN;55555;) is used in obtaining the pseudorandom deviates.
#include <imsls.h>
#include <stdio.h>
void main()
{
int nran = 10000, n_run = 10;
float *x, pvalue, *pairs_counts, expect, chisq, df;
imsls_random_seed_set(123467);
x = imsls_f_random_uniform(nran, 0);
pvalue = imsls_f_randomness_test(nran, x, n_run,
IMSLS_CHI_SQUARED, &chisq,
IMSLS_DF, &df,
IMSLS_EXPECT, &expect,
IMSLS_PAIRS, 5, &pairs_counts,
0);
imsls_f_write_matrix("pairs_counts", n_run, n_run, pairs_counts, 0);
printf("expect = %8.2f\n", expect);
printf("chisq = %8.2f\n", chisq);
printf("df = %8.2f\n", df);
printf("pvalue = %10.4f\n", pvalue);
}
Output
pairs_counts
1
2 3 4 5
6 7
8 9 10
1
112 82 95 118
103 103 113 84
90 74
2 104 106 109 108 101 98 102 92 109 88
3 88 111 86 106 112 79 103 105 106 101
4 91 110 108 92 88 108 113 93 105 114
5 104 105 103 104 101 94 96 87 93 104
6 98 104 103 104 79 89 92 104 92 100
7 103 91 97 101 116 83 118 118 106 99
8 105 105 111 91 93 82 100 104 110 89
9 92 102 82 101 94 128 102 110 125 98
10 79 99 103 98 104 101 93 93 98 105
expect = 99.95
chisq = 104.86
df = 99.00
pvalue = 0.3242
Example 3
In the following example, 2000 observations generated via IMSL routine imsls_f_random_uniform (Chapter 12, “Random Number Generation”.p<.STCH18.DOC!RNUN;55;) are input to IMSLS_DSQAR in one call. In the example, the null hypothesis of a uniform distribution is not rejected.
#include <imsls.h>
#include <stdio.h>
void main()
{
int nran = 2000, n_run = 6;
float *x, pvalue, *dsquare_counts, *covariances, expect, chisq, df;
imsls_random_seed_set(123457);
x = imsls_f_random_uniform(nran, 0);
pvalue = imsls_f_randomness_test(nran, x, n_run,
IMSLS_CHI_SQUARED, &chisq,
IMSLS_DF, &df,
IMSLS_EXPECT, &expect,
IMSLS_DSQUARE, &dsquare_counts,
0);
imsls_f_write_matrix("dsquare_counts", 1, n_run, dsquare_counts, 0);
printf("expect = %10.4f\n", expect);
printf("chisq = %10.4f\n", chisq);
printf("df = %8.2f\n", df);
printf("pvalue = %10.4f\n", pvalue);
}
Output
dsquare_counts
1
2 3
4 5
6
87
84 78
76 92
83
expect =
83.3333
chisq =
2.0560
df =
5.00
pvalue = 0.8413
Example 4
In the following example, 2001 deviates generated by IMSL routine imsls_f_random_uniform (Chapter 12, “Random Number Generation”.p<.STCH18.DOC!RNUN;;) are input to IMSLS_DCUBE, and tabulated in 27 equally sized cubes. In the example, the null hypothesis is not rejected.
#include <imsls.h>
#include <stdio.h>
void main()
{
int nran = 2001, n_run = 3;
float *x, pvalue, *dcube_counts, expect, chisq, df;
imsls_random_seed_set(123457);
x = imsls_f_random_uniform(nran, 0);
pvalue = imsls_f_randomness_test(nran, x, n_run,
IMSLS_CHI_SQUARED, &chisq,
IMSLS_DF, &df,
IMSLS_EXPECT, &expect,
IMSLS_DCUBE, &dcube_counts,
0);
imsls_f_write_matrix("dcube_counts", n_run, n_run, dcube_counts, 0);
imsls_f_write_matrix("dcube_counts", n_run, n_run, &dcube_counts[n_run*n_run], 0);
imsls_f_write_matrix("dcube_counts", n_run, n_run, &dcube_counts[2*n_run*n_run], 0);
printf("expect = %10.4f\n", expect);
printf("chisq = %10.4f\n", chisq);
printf("df = %8.2f\n", df);
printf("pvalue = %10.4f\n", pvalue);
}
Output
dcube_counts
1 2
3
1 26 27
24
2 20
17 32
3
30 18
21
dcube_counts
1 2
3
1 20
16 26
2
22 22
27
3 30
24 26
dcube_counts
1 2
3
1 28
30 22
2
23 24
22
3 33
30 27
expect =
24.7037
chisq =
21.7631
df =
26.0000
pvalue = 0.701586
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |