Analyzes data from strip-plot experiments. Function strip_plot also analyzes strip-plot experiments replicated at several locations.

Synopsis

#include <imsls.h>

float * imsls_f_strip_plot (int n, int n_locations, int n_strip_a,
int n_strip_b, int block[], int strip_a[], int strip_b[],
float y[],…, 0)

The type double function  is imsls_d_strip_plot.

Required Arguments

int n  (Input)
Number of missing and non-missing experimental observations. imsls_f_strip_plot verifies that:

 

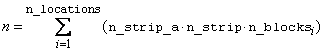
int n_locations (Input)
Number of locations.  n_locations must be one or greater.   If n_locations>1 then the optional array locations[] must be included as input to imsls_f_strip_plot. See optional argument IMSLS_LOCATIONS.

int n_strip_a  (Input)
Number of levels associated with the strip factor A.  n_strip_a must be greater than one.

int n_strip_b  (Input)
Number of levels associated with the strip factor B.  n_strip_b must be greater than one.

int block[]  (Input)

            An array of length n containing the block identifiers for each observation in y.  Locations can have different numbers of blocks.  Each block at a single location must be assigned a different identifier, but different locations can have the same assignments.

int strip_a[]  (Input)
An array of length n containing the factor A strip-plot identifiers for each observation in y.  Each level of this factor must be assigned a different integer.  This routine verifies that the number of unique factor A strip-plot identifiers is equal to n_strip_a.

int strip_b[]  (Input)
An array of length n containing the factor B strip-plot identifiers for each observation in y.  Each level of this factor must be assigned a different integer.  This routine verifies that the number of unique factor B strip-plot identifiers is equal to n_strip_b.

float y[] (Input)
An array of length n containing the experimental observations and any missing values.  Missing values cannot be omitted.  They are indicated by placing a NaN (not a number) in y. The NaN value can be set using either the function imsls_f_machine(6) or imsls_d_machine(6), depending upon whether single or double precision is being used, respectively.  The location, strip-plot A, and strip-plot B for each observation in y are identified by the corresponding values in the arguments locations, strip_a, and strip_b.

Return Value

Address of a pointer to the memory location of a two dimensional, 12 by 6 array containing the ANOVA table.  Each row in this array contains values for one of the effects in the ANOVA table.  The first value in each row,
anova_table_i,0 = anova_table[i*6], identifies the source for the effect associated with values in that row.  The remaining values in a row contain the ANOVA table values using the following convention:

 

 

The Source Identifiers in the first column of anova_table_i,j are the only negative values in anova_table. Assignments of identifiers to ANOVA sources use the following coding:

 

 

Notes: † If n_locations=1 sources involving location are set to missing (NaN).

Synopsis with Optional Arguments

#include <imsl.h>

float * imsls_f_strip_plot (int n, int n_locations, int n_strip_a, int n_strip_b, int block[], int strip_a[], int strip_b[], float y[],
IMSLS_RETURN_USER, float anova_table[],
IMSLS_LOCATIONS, int locations[],
IMSLS_N_MISSING, int *n_missing,
IMSLS_CV,  float **cv,
IMSLS_CV_USER, float cv[],
IMSLS_GRAND_MEAN, float *grand_mean,
IMSLS_STRIP_PLOT_A_MEANS, float **strip_plot_a_means,
IMSLS_STRIP_PLOT_A_MEANS_USER,
                                                                       float strip_plot_a_means[],
IMSLS_STRIP_PLOT_B_MEANS, float **strip_plot_b_means,
IMSLS_STRIP_PLOT_B_MEANS_USER,
                                                                       float strip_plot_b_means[],
IMSLS_TREATMENT_MEANS, float **treatment_means,
IMSLS_TREATMENT_MEANS_USER, float treatment_means[],
IMSLS_STD_ERRORS, float **std_err,
IMSLS_STD_ERRORS_USER, float std_err[],
IMSLS_N_BLOCKS int **n_blocks,
IMSLS_N_BLOCKS_USER, int n_blocks[],
IMSLS_LOCATION_ANOVA_TABLE float **location_anova_table,
IMSLS_LOCATION_ANOVA_TABLE_USER,
                                                                       float location_anova_table[],
IMSLS_ANOVA_ROW_LABELS, char ***anova_row_labels,
IMSLS_ANOVA_ROW_LABELS_USER, char *anova_row_labels[],

     0)

Optional Arguments

IMSLS_RETURN_USER, float anova_table[] (Output)
User defined array of length 72 for storage of the 12 by 6 ANOVA table described as the return argument for imsls_f_strip_plot.  For a detailed description of the format for this table, see the previous description of the return arguments for imsls_f_strip_plot.

IMSLS_LOCATIONS, int locations[]  (Input)
An array of length n containing the location identifiers for each observation in y.  Unique integers must be assigned to each location in the study.  This argument is required when n_locations>1.

IMSLS_N_MISSING, int *n_missing  (Output)
Number of missing values, if any, found in y.   Missing values are denoted with a NaN (Not a Number) value.

IMSLS_CV, float **cv (Output)
Address of a pointer to  an internally allocated array of length 3 containing the whole-plot, split-plot and sub-plot coefficients of variation.  cv[0] contains the whole-plot C.V., cv[1] contains the split-plot C.V., and cv[2] contains the sub-plot C.V.

IMSLS_CV_USER, float cv[] (Output)
Storage for the array cv, provided by the user.

IMSLS_GRAND_MEAN, float *grand_mean (Output)
Mean of all the data across every location.

IMSLS_STRIP_PLOT_A_MEANS, float **strip_plot_a_means (Output)
Address of a pointer to an internally allocated array of length n_strip_a containing the factor A strip-plot means.

IMSLS_STRIP_PLOT_A_MEANS_USER, float strip_plot_a_means [] (Output)
Storage for the array strip_plot_a_means, provided by the user.

IMSLS_STRIP_PLOT_B_MEANS, float **strip_plot_b_means (Output)
Address of a pointer to an internally allocated array of length n_strip_b containing the factor B strip-plot means.

IMSLS_STRIP_PLOT_B_MEANS_USER, float strip_plot_b_means [] (Output)
Storage for the array strip_plot_b_means, provided by the user.

IMSLS_TREATMENT_MEANS, float **treatment_means (Output)
Address of a pointer to an internally allocated array of size (n_split_a×n_split_b) containing the treatment means.
For i > 0 and  j > 0, treatment_means_i,j = treatment_means
[(i-1)×n_split_a +(j-1)] contains the mean of the observations, averaged over all locations, blocks and replicates, for the ith level of the factor A strip-plot and  the jth level of the factor B strip-plot.

IMSLS_TREATMENT_MEANS_USER, float treatment_means[]  (Output)
Storage for the array treatment_means, provided by the user.

IMSLS_STD_ERRORS, float **std_err (Output)
Address of a pointer to an internally allocated array of length 10 containing five standard errors and their associated degrees of freedom.   The standard errors are in the first five elements and their associated degrees of freedom are reported in std_err[5] through std_err[9].

 

Element	Standard Error for Comparisons Between Two	Degrees of Freedom
std_err[0]	Factor A Strip-Plot Means	std_err[5]
std_err[1]	Factor B Strip-Plot Means	std_err[6]
std_err[2]	Factor A Strip-Plot Means at the same level of Factor B	std_err[7]
std_err[3]	Factor B Strip-Plot Means at the same level of Factor A	std_err[8]
std_err[4]	Treatment Means  (same strip-plot A and strip-plot B)	std_err[9]

IMSLS_STD_ERRORS_USER, float std_err[] (Output)
Storage for the array std_err, provided by the user.

IMSLS_N_BLOCKS, int **n_blocks (Output)
Address of a pointer to an internally allocated array of length n_locations containing the number of blocks, or replicates, at each location.

IMSLS_N_BLOCKS_USER, int n_blocks[] (Output)
Storage for the array n_blocks, provided by the user.

IMSLS_LOCATION_ANOVA_TABLE, float **location_anova_table (Output)
Address of a pointer to an internally allocated 3-dimensional array of size n_locations  by 12 by 6 containing the Anova tables associated with each location.  For each location, the 12 by 6 dimensional array corresponds to the Anova table for that location.  For example, location_anova_table[(i-1)×72+(j-1)×6 + (k-1)] contains the value in the kth column and jth row of the returned Anova table for the ith location.

IMSLS_LOCATION_ANOVA_TABLE_USER, float anova_table[] (Output)
Storage for the array location_anova_table, provided by the user.

IMSLS_ANOVA_ROW_LABELS, char ***anova_row_labels   (Output)
Address of a pointer to a pointer to an internally allocated array containing the labels for each of the  n_anova rows of the returned ANOVA table.  The label for the ith row of the ANOVA table can be printed with

printf("%s", anova_row_labels[i]);

The memory associated with anova_row_labels  can be freed with a single call to free(anova_row_labels).

IMSLS_ANOVA_ROW_LABELS_USER, char *anova_row_labels[]   (Output)
Storage for the array anova_row_labels, provided by the user.  The amount of space required will vary depending upon the number of factors and n_anova.  An upperbound on the required memory is
char *anova_row_labels[600].

Description

Function imsls_f_strip_plot is capable of analyzing a wide variety of strip-plot experiments. 

The essential distinction between strip-plot and split-plot experiments is the application of factor B.  In a split-plot experiment, levels of Factor B are nested within Factor A, see Table 2 below.  In strip-plot experiments, Factors A and B are completely crossed, see Figure 1 below.  This occurs, for example, when an agricultural field is used as a block and the levels of factor A are applied in vertical strips across the entire field. Levels of factor B are assigned to horizontal strips across the same block.

 

Table 1 – Strip-Plot Experiments – Strip-Plots Completely Crossed

 

Table 2 – Split-Plot Experiments – Split-Plot B Nested within Strip-Plot A

In some studies, a strip-plot experiment is replicated at several locations.  Imsls_f_strip_plot can analyze strip-plot experiments replicated at multiple locations, even when the number of blocks or replicates at each location are different.  If only a single replicate or block is used at each location, then location should be treated as a blocking factor, with n_locations set equal to one.   If n_locations=1, it is assumed that the experiment was conducted at a single location with more than one block or replicate at that location.  In this case, the four entries associated with location in the ANOVA table will contain missing values.

However, if n_locations>1, it is assumed the experiment was repeated at multiple locations, with blocking occurring at each location.  Although the number of blocks at each location can be different, the number of levels for the factor A and B strip-plots must be the same at each location.  The locations associated with each of the observations in y are specified in the argument locations[], which is a required input argument when n_locations>1. 

Locations are assumed to be random effects, then tests involving factor A strip-plots use the interaction between factor A strip-plots and locations as the error term for testing whether there are statistically significant differences among the levels of factor A.  However, this assumes that the interaction of factor A and locations is not statistically significant.  A test of this assumption is included in the ANOVA table.  If the interaction between factor A strip-plots and locations is statistically significant, then the nature of that interaction should be explored since it impacts the interpretation of the significance of the factor A.

Similarly, when locations are assumed to be random effects, tests involving factor B do not use the strip-plot B errors pooled across locations.  Instead, the error term for factor B is the interaction between locations and factor B. 

Example

This example uses data from a strip-plot design with two levels for the first strip and four for the last strip.

#include <stdlib.h>

#include <math.h>

#include "imsls.h"

 

void main()

{

 

  char *col_labels[] = {" ", "\nID", "\nDF", "\nSSQ",

                        "Mean\nsquares", "\nF", "\np-value"};

  char **anova_row_labels = NULL;

  int i, j, k, l, page_width = 132;

  int n = 24;                /* Total number of observations */

  int n_locations = 1;       /* Number of locations */

  int n_strip_a   = 2;       /* Number of factor A strip-plots within a location */

  int n_strip_b   = 4;       /* Number of factor B strip-plots within a location */

 

  int block[]={

    1, 1, 1, 1, 1, 1, 1, 1,

    2, 2, 2, 2, 2, 2, 2, 2,

    3, 3, 3, 3, 3, 3, 3, 3};

  int strip_a[]={

    1, 1, 1, 1, 2, 2, 2, 2,

    1, 1, 1, 1, 2, 2, 2, 2,

    1, 1, 1, 1, 2, 2, 2, 2};

  int strip_b[]={

    1, 2, 3, 4, 1, 2, 3, 4,

    1, 2, 3, 4, 1, 2, 3, 4, 

    1, 2, 3, 4, 1, 2, 3, 4};

  float y[] ={

    30.0, 40.0, 38.9, 38.2,

    41.8, 52.2, 54.8, 58.2,

    20.5, 26.9, 21.4, 25.1,

    26.4, 36.7, 28.9, 35.9,

    21.0, 25.4, 24.0, 23.3,

    34.4, 41.0, 33.0, 34.9};

  float grand_mean=0;

  float *cv;

  float *aov;

  float *treatment_means;

  float *strip_plot_a_means;

  float *strip_plot_b_means;

  float *std_err;

  int n_missing;

  int *equal_means;

 

  aov = imsls_f_strip_plot(n, n_locations, n_strip_a, n_strip_b,

                           block, strip_a, strip_b, y,

                           IMSLS_GRAND_MEAN, &grand_mean,

                           IMSLS_CV, &cv,

                           IMSLS_N_MISSING,  &n_missing, 

                           IMSLS_STRIP_PLOT_A_MEANS, &strip_plot_a_means,

                           IMSLS_STRIP_PLOT_B_MEANS, &strip_plot_b_means,

                           IMSLS_TREATMENT_MEANS, &treatment_means,

                           IMSLS_STD_ERRORS,  &std_err,

                           IMSLS_ANOVA_ROW_LABELS, &anova_row_labels,

                           0);

 

  /* Output results. */

  imsls_page(IMSLS_SET_PAGE_WIDTH, &page_width);

 

  /* Print ANOVA table. */

  imsls_f_write_matrix("   *** ANALYSIS OF VARIANCE TABLE ***",

                       12, 6, aov,

                       IMSLS_WRITE_FORMAT, "%3.0f%3.0f%8.2f%7.2f%7.2f%7.3f",

                       IMSLS_ROW_LABELS, anova_row_labels,

                       IMSLS_COL_LABELS, col_labels,

                       0);

 

  printf("\nGrand mean: %f\n", grand_mean);

 

  /* Print treatment means */

  imsls_f_write_matrix("Treatment Means", n_strip_a, n_strip_b,

                       treatment_means, 0);

  printf("\n\nStandard Error for Comparing Two Treatment Means: \n");

  printf("  Same Level of Factor B          %f (df=%f)\n",

         std_err[2], std_err[7]);

  printf("  Same Level of Factor A          %f (df=%f)\n",

         std_err[3], std_err[8]);

  printf("  Different Factor A and B Levels %f (df=%f)\n\n\n\n",

         std_err[4], std_err[9]);

 

 

  /* Print factor A means */

  imsls_f_write_matrix("Factor A Means", n_strip_a, 1,

                       strip_plot_a_means, 0);

  printf("\nStandard Error for Comparing Two Factor A Means: \n  %f (df=%f)\n",

         std_err[0], std_err[5]);

  equal_means = imsls_f_multiple_comparisons(n_strip_a, strip_plot_a_means,          std_err[5],

                                             std_err[0]/sqrt(2),

                                             IMSLS_LSD,

                                             IMSLS_ALPHA, .05,

                                             0);

  /* Print multiple comparison results */

  imsls_i_write_matrix("LSD Comparison : Size of Groups of Means", 1, n_strip_a-1,

      equal_means, 0);

 

 

  /* Print factor B means */

  imsls_f_write_matrix("\n\nFactor B Means", n_strip_b, 1,

                       strip_plot_b_means, 0);

  printf("\nStandard Error for Comparing Two Factor B Means: \n  %f (df=%f)\n",

         std_err[1], std_err[6]);

  equal_means = imsls_f_multiple_comparisons(n_strip_b, strip_plot_b_means, std_err[6],

                                             std_err[1]/sqrt(2),

                                             IMSLS_LSD,

                                             IMSLS_ALPHA, .05,

                                             0);

  /* Multiple comparison results */

  imsls_i_write_matrix("LSD Comparison : Size of Groups of Means",

                       1, n_strip_b-1, equal_means, 0);

}

 

Output

 

 

                         *** ANALYSIS OF VARIANCE TABLE ***

                                                          Mean

                                    ID   DF       SSQ  squares        F  p-value

Location                            -1  ...  ........  .......  .......  .......

Block Within Location               -2    2   1310.28   655.14    19.89    0.009

Strip-Plot A                        -3    1    858.01   858.01    40.37    0.024

Location x Strip-Plot A             -4  ...  ........  .......  .......  .......

Strip-Plot A Error                  -5    2     42.51    21.26     4.62    0.061

Strip-Plot B                        -6    3    227.73    75.91     4.66    0.052

Location x Strip-Plot B             -7  ...  ........  .......  .......  .......

Strip-Plot B Error                  -8    6     97.76    16.29     3.54    0.075

Strip-Plot A x Strip-Plot B         -9    3     13.40     4.47     0.97    0.466

Location x Strip-Plot A            -10  ...  ........  .......  .......  .......

   x Strip-Plot B

Strip-Plot A x Strip-Plot B Error  -11    6     27.63     4.60  .......  .......

Corrected Total                    -12   23   2577.33  .......  .......  .......

 

 

Grand mean: 33.870834

 

 

 

                   Treatment Means

             1            2            3            4

1        23.83        30.77        28.10        28.87

2        34.20        43.30        38.90        43.00

 

 

Standard Error for Comparing Two Treatment Means:

  Same Level of Factor B          2.417643 (df=4.772558)

  Same Level of Factor A          2.639322 (df=9.140633)

  Different Factor A and B Levels 3.121075 (df=8.405353)

 

 

Factor A Means

1        27.89

2        39.85

 

Standard Error for Comparing Two Factor A Means:

  1.882171 (df=2.000000)

 

LSD Comparison : Size of Groups of Means

                    0

 

Factor B Means

1        29.02

2        37.03

3        33.50

4        35.93

 

Standard Error for Comparing Two Factor B Means:

  2.330465 (df=6.000000)

 

LSD Comparison : Size of Groups of Means

                1   2   3

                2   3   0

 

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260