Detects and determines outliers and simultaneously estimates the model parameters in a time series whose underlying outlier free series follows a general seasonal or nonseasonal ARMA model.
Synopsis
float
*imsls_f_ts_outlier_identification
(int n_obs, int
model[],
float
w[],Ö,0)
The type double function is imsls_d_ts_outlier_identification.
Required Arguments
int n_obs
(Input)
Number of observations in the time series.
int model[]
(Input)
Vector of length 4 containing the numbers
p, q, s, d of the ARIMA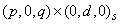 model the outlier free series is
following.
model the outlier free series is
following.
float w[]
(Input)
An array of length n_obs containing the
time series.
Return Value
Pointer to an array of length n_obs
containing the outlier free time series.
If an error occurred, NULL
is returned.
Synopsis with Optional Arguments
float
*imsls_f_ts_outlier_identification (int
n_obs,
int model[], float w[],
IMSLS_RETURN_USER, float x[],
IMSLS_DELTA, float
delta,
IMSLS_CRITICAL, float critical,
IMSLS_EPSILON, float
epsilon,
IMSLS_RELATIVE_ERROR, float relative_error,
IMSLS_RESIDUAL, float
**residual,
IMSLS_RESIDUAL_USER, float
residual[],
IMSLS_RESIDUAL_SIGMA, float
*res_sigma,
IMSLS_NUM_OUTLIERS, int
*num_outliers,
IMSLS_OUTLIER_STATISTICS, int
**outlier_stat,
IMSLS_OUTLIER_STATISTICS_USER, int
outlier_stat[],
IMSLS_TAU_STATISTICS, float
**tau_stat,
IMSLS_TAU_STATISTICS_USER, float
tau_stat[],
IMSLS_OMEGA_WEIGHTS, float
**omega,
IMSLS_OMEGA_WEIGHTS_USER, float omega[],
IMSLS_ARMA_PARAM,
float **parameters,
IMSLS_ARMA_PARAM_USER, float
parameters[],
IMSLS_AIC, float *aic,
0)
Optional Arguments
IMSLS_RETURN_USER, float x[] (Output)
A user supplied array of length n_obs
containing the outlier free series.
IMSLS_DELTA, float delta (Input)
The
dampening effect parameter used in the detection of a Temporary Change Outlier (TC), 0<delta <
1.
Default: delta = 0.7
IMSLS_CRITICAL, float critical (Input)
Critical value
used as a threshold for outlier detection, critical >
0.
Default: critical =
3.0
IMSLS_EPSILON, float epsilon
(Input)
Positive tolerance value controlling
the accuracy of parameter estimates during outlier detection.
Default: epsilon = 0.001
IMSLS_RELATIVE_ERROR,
float relative_error
(Input)
Stopping criterion
for the nonlinear equation solver used in function imsls_f_arma.
Default: relative_error =
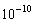 .
.
IMSLS_RESIDUAL, float **residual (Output)
Address of a
pointer to an internally allocated array of length n_obs containing the
residuals for the outlier free series.
IMSLS_RESIDUAL_USER, float residual[] (Output)
Storage for array
residual is provided
by the user. See IMSLS_RESIDUAL.
IMSLS_RESIDUAL_SIGMA, float *res_sigma (Output)
Residual standard
error of the outlier free series.
IMSLS_NUM_OUTLIERS, int *num_outliers (Output)
The number of
outliers detected.
IMSLS_OUTLIER_STATISTICS, int **outlier_stat (Output)
Address of a
pointer to an internally allocated array of length num_outliers ī 2 containing
outlier statistics. The first column contains the time at which the
outlier was observed (t=1,2,...,n_obs) and the second column contains an identifier indicating the
type of outlier observed.
Outlier types fall into one of five
categories:
Use IMSLS_NUM_OUTLIERS to obtain IMSLS_NUM_OUTLIERS, the number of detected outliers. If num_outliers = 0, NULL is returned.
IMSLS_OUTLIER_STATISTICS_USER,
int outlier_stat[]
(Output)
A user allocated
array of length n_obs ī 2 containing outlier
statistics in the first num_outliers
locations. See IMSLS_OUTLIER_STATISTICS.
If
num_outliers = 0, outlier_stat stays
unchanged.
IMSLS_TAU_STATISTICS,
float **tau_stat
(Output)
Address of a
pointer to an internally allocated array of length num_outliers containing the t value for each detected
outlier.
If num_outliers = 0, NULL is returned.
IMSLS_TAU_STATISTICS_USER,
float tau_stat[] (Output)
A user allocated
array of length n_obs containing the t value for each detected outlier in
its first num_outliers
locations.
If num_outliers = 0, tau_stat stays
unchanged.
IMSLS_OMEGA_WEIGHTS,
float **omega (Output)
Address of a
pointer to an internally allocated array of length num_outliers
containing the computed
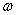 weights for the detected
outliers.
weights for the detected
outliers.
If num_outliers = 0, NULL is returned.
IMSLS_OMEGA_WEIGHTS_USER
float omega[] (Output)
A user allocated
array of length n_obs containing the
computed 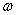 weights for the
detected outliers in its first num_outliers locations.
weights for the
detected outliers in its first num_outliers locations.
If num_outliers = 0, omega stays
unchanged.
IMSLS_ARMA_PARAM,
float **parameters
(Output)
Address of a pointer to an internally allocated array of
length 1+p+q containing the estimated constant, AR and MA
parameters.
IMSLS_ARMA_PARAM_USER
float parameters[]
(Output)
A user allocated
array of length 1+p+q containing the estimated constant, AR and MA
parameters.
IMSLS_AIC,
float *aic (Output)
Akaikeís
information criterion (AIC).
Description
Consider a univariate time series 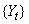 that can be described by the
following multiplicative seasonal ARIMA model of order
that can be described by the
following multiplicative seasonal ARIMA model of order 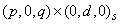 :
:
Here, 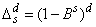 ,
, 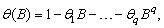
 .
.
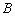 is the lag
operator,
is the lag
operator, 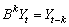 ,
,  is a white noise process, and
is a white noise process, and 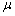 denotes the mean of the
series
denotes the mean of the
series 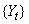 .
.
In general, 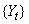 is not directly observable due to the influence of
outliers. Chen and Liu (1993) distinguish between four types of outliers:
innovational outliers (IO), additive outliers (AO), temporary changes (TC)
and level shifts (LS). If an outlier occurs as the last observation of the
series, then Chen and Liuís algorithm is unable to determine the outlierís
classification. In imsls_f_ts_outlier_identification,
such an outlier is called a UI (unable to identify) and is treated as an
innovational outlier.
is not directly observable due to the influence of
outliers. Chen and Liu (1993) distinguish between four types of outliers:
innovational outliers (IO), additive outliers (AO), temporary changes (TC)
and level shifts (LS). If an outlier occurs as the last observation of the
series, then Chen and Liuís algorithm is unable to determine the outlierís
classification. In imsls_f_ts_outlier_identification,
such an outlier is called a UI (unable to identify) and is treated as an
innovational outlier.
In order to take the effects of multiple outliers occurring
at time points  into account, Chen and Liu consider the following model:
into account, Chen and Liu consider the following model:
Here, 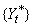 is the observed outlier contaminated series, and
is the observed outlier contaminated series, and 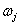 and
and  denote the magnitude and
dynamic pattern of outlier
denote the magnitude and
dynamic pattern of outlier 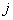 , respectively.
, respectively. 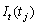 is an indicator function that determines the temporal
course of the outlier effect,
is an indicator function that determines the temporal
course of the outlier effect,  ,
, 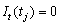 otherwise. Note that
otherwise. Note that  operates on
operates on 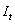 via
via 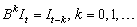 .
.
The last formula shows that the outlier free series
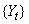 can be obtained
from the original series
can be obtained
from the original series 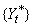 by removing all occurring outlier effects:
by removing all occurring outlier effects:
The different types of outliers are charaterized by
different values for  :
:
1. 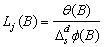 for an innovational outlier,
for an innovational outlier,
3. 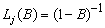 for a level shift outlier
and
for a level shift outlier
and
4. 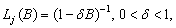 for a temporary change outlier.
for a temporary change outlier.
Function imsls_f_ts_outlier_identification
is an implementation of Chen and Liuís algorithm. It determines the coefficients
in 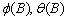 and the outlier
effects in the model for the observed series jointly in three stages. The
magnitude of the outlier effects is determined by least squares estimates.
Outlier detection itself is realized by examination of the maximum value of the
standardized statistics of the outlier effects. For a detailed description, see
Chen and Liuís original paper (1993).
and the outlier
effects in the model for the observed series jointly in three stages. The
magnitude of the outlier effects is determined by least squares estimates.
Outlier detection itself is realized by examination of the maximum value of the
standardized statistics of the outlier effects. For a detailed description, see
Chen and Liuís original paper (1993).
Intermediate and final estimates for the coefficients in
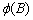 and
and 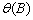 are computed by functions imsls_f_arma and imsls_f_max_arma. If the roots of
are computed by functions imsls_f_arma and imsls_f_max_arma. If the roots of 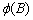 or
or 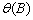 lie on or within the unit
circle, then the algorithm stops with an appropriate error message. In this
case, different values for p and q should be tried.
lie on or within the unit
circle, then the algorithm stops with an appropriate error message. In this
case, different values for p and q should be tried.
Examples
Example 1
This example is based on estimates of the Canadian lynx
population. Function imsls_f_ts_outlier_identification
is used to fit an ARIMA(2,2,0) model of the form ,
, 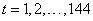 ,
, Gaussian White noise, to the given series. Function ts_outlier_identification computes
parameters
Gaussian White noise, to the given series. Function ts_outlier_identification computes
parameters 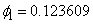 and
and
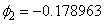 and identifies a
LS outlier at time point
and identifies a
LS outlier at time point 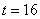 .
.
0.24300E01,0.25060E01,0.27670E01,0.29400E01,0.31690E01,0.34500E01,
0.35940E01,0.37740E01,0.36950E01,0.34110E01,0.27180E01,0.19910E01,
0.22650E01,0.24460E01,0.26120E01,0.33590E01,0.34290E01,0.35330E01,
0.32610E01,0.26120E01,0.21790E01,0.16530E01,0.18320E01,0.23280E01,
0.27370E01,0.30140E01,0.33280E01,0.34040E01,0.29810E01,0.25570E01,
0.25760E01,0.23520E01,0.25560E01,0.28640E01,0.32140E01,0.34350E01,
0.34580E01,0.33260E01,0.28350E01,0.24760E01,0.23730E01,0.23890E01,
0.27420E01,0.32100E01,0.35200E01,0.38280E01,0.36280E01,0.28370E01,
0.24060E01,0.26750E01,0.25540E01,0.28940E01,0.32020E01,0.32240E01,
0.33520E01,0.31540E01,0.28780E01,0.24760E01,0.23030E01,0.23600E01,
0.26710E01,0.28670E01,0.33100E01,0.34490E01,0.36460E01,0.34000E01,
0.25900E01,0.18630E01,0.15810E01,0.16900E01,0.17710E01,0.22740E01,
0.25760E01,0.31110E01,0.36050E01,0.35430E01,0.27690E01,0.20210E01,
0.21850E01,0.25880E01,0.28800E01,0.31150E01,0.35400E01,0.38450E01,
0.38000E01,0.35790E01,0.32640E01,0.25380E01,0.25820E01,0.29070E01,
0.31420E01,0.34330E01,0.35800E01,0.34900E01,0.34750E01,0.35790E01,
0.28290E01,0.19090E01,0.19030E01,0.20330E01,0.23600E01,0.26010E01,
0.30540E01,0.33860E01,0.35530E01,0.34680E01,0.31870E01,0.27230E01,
0.26860E01,0.28210E01,0.30000E01,0.32010E01,0.34240E01,0.35310E01};
float *parameters = NULL, *result = NULL;
result = imsls_f_ts_outlier_identification(n_obs, model, series,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS, &outlier_stat,
IMSLS_ARMA_PARAM, ¶meters,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
printf("Number of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n");
printf("Time point\t\tOutlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d\t\t%d\n", outlier_stat[2*i], outlier_stat[2*i+1]);
for (i=0; i<=model[0]+model[1]; i++)
printf("%d\t\t%lf\n", i, parameters[i]);
printf("RSE:%lf\n", res_sigma);
Output
time point original series outlier free series
Example 2
This example is an artificial realization of an ARMA(1,1)
process via formula 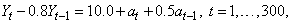
 Gaussian white noise,
Gaussian white noise,
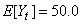 .
.
An additive outlier with 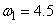 was added at time point
was added at time point
 , a temporary change
outlier with
, a temporary change
outlier with 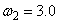 was
added at time point
was
added at time point 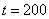 .
.
float parameters_user[300], result_user[300];
50.0000000,50.2728081,50.6242599,51.0373917,51.9317627,50.3494759,
51.6597252,52.7004929,53.5499802,53.1673279,50.2373505,49.3373871,
49.5516472,48.6692696,47.6606636,46.8774185,45.7315445,45.6469727,
45.9882355,45.5216560,46.0479660,48.1958656,48.6387749,49.9055367,
49.8077278,47.7858467,47.9386749,49.7691956,48.5425873,49.1239853,
49.8518791,50.3320694,50.9146347,51.8772049,51.8745689,52.3394470,
52.7273712,51.4310036,50.6727448,50.8370399,51.2843437,51.8162918,
51.6933670,49.7038231,49.0189247,49.455703,50.2718010,49.9605980,
51.3775749,50.2285385,48.2692299,47.6495590,49.2938499,49.1924858,
49.6449242,50.0446815,51.9972496,54.2576981,52.9835434,50.4193535,
50.3617897,51.8276901,53.1239929,54.0682144,54.9238319,55.6877632,
54.8896332,54.0701065,52.2754097,52.2522354,53.1248703,51.1287193,
50.5003815,49.6504173,47.2453079,45.4555626,45.8449707,45.9765129,
45.7682228,45.2343674,46.6496811,47.0894432,49.3368340,50.8058052,
49.9132500,49.5893288,48.2470627,46.9779968,45.6760864,45.7070389,
46.6158409,47.5303612,47.5630417,47.0389214,46.0352287,45.8161545,
45.7974396,46.0015373,45.3796463,45.3461685,47.6444016,49.3327446,
49.3810692,50.2027817,51.4567032,52.3986320,52.5819206,52.7721825,
52.6919098,53.3274345,55.1345940,56.8962631,55.7791634,55.0616989,
52.3551178,51.3264084,51.0968323,51.1980476,52.8001442,52.0545082,
50.8742943,51.5150337,51.2242050,50.5033989,48.7760124,47.4179192,
49.7319527,51.3320541,52.3918304,52.4140434,51.0845947,49.6485748,
50.6893463,52.9840813,53.3246994,52.4568024,51.9196091,53.6683121,
53.4555359,51.7755814,49.2915611,49.8755112,49.4546776,48.6171913,
49.9643021,49.3766441,49.2551308,50.1021881,51.0769119,55.8328133,
52.0212708,53.4930801,53.2147255,52.2356453,51.9648819,52.1816330,
51.9898071,52.5623627,51.0717278,52.2431946,53.6943054,54.3752098,
54.1492615,53.8523254,52.1093712,52.3982697,51.2405128,50.3018112,
51.3819618,49.5479546,47.5024452,47.4447708,47.8939056,48.4070015,
48.2440681,48.7389755,49.7309227,49.1998024,49.5798340,51.1196213,
50.6288414,50.3971405,51.6084099,52.4564743,51.6443901,52.4080658,
52.4643364,52.6257210,53.1604691,51.9309731,51.4137230,52.1233368,
52.9867249,53.3180733,51.9647636,50.7947655,52.3815842,50.8353729,
49.4136009,52.8355217,52.2234840,51.1392517,48.5245132,46.8700218,
46.1607285,45.2324257,47.4157829,48.9989090,49.6230736,50.4352913,
51.1652985,50.2588654,50.7820129,51.0448799,51.2880516,49.6898804,
49.0288200,49.9338837,48.2214432,46.2103348,46.9550171,47.5595894,
47.7176018,48.4502945,50.9816895,51.6950073,51.6973495,52.1941261,
51.8988075,52.5617599,52.0218391,49.5236053,47.9684906,48.2445183,
48.8275146,49.7176971,51.5649338,52.5627213,52.0182419,50.9688835,
51.5846901,50.9486771,48.8685837,48.5600624,48.4760094,48.5348396,
50.4187813,51.2542381,50.1872864,50.4407692,50.6222687,50.4972000,
51.0036087,51.3367500,51.7368202,53.0463791,53.6261253,52.0728683,
48.9740753,49.3280830,49.2733917,49.8519020,50.8562126,49.5594254,
49.6109200,48.3785629,48.0026474,49.4874268,50.1596375,51.8059540,
53.0288620,51.3321075,49.3114815,48.7999306,47.7201881,46.3433914,
46.5303612,47.6294632,48.6012459,47.8567657,48.0604057,47.1352806,
49.5724792,50.5566483,49.4182968,50.5578079,50.6883736,50.6333389,
51.9766159,51.0595245,49.3751640,46.9667702,47.1658173,47.4411278,
47.5360374,48.9914742,50.4747620,50.2728043,51.9117165,53.7627792};
imsls_f_ts_outlier_identification(n_obs, model, series,
IMSLS_NUM_OUTLIERS, &num_outliers,
IMSLS_OUTLIER_STATISTICS_USER, outlier_stat_user,
IMSLS_OMEGA_WEIGHTS_USER, omega_user,
IMSLS_ARMA_PARAM_USER, parameters_user,
IMSLS_RETURN_USER, result_user,
IMSLS_RESIDUAL_SIGMA, &res_sigma,
IMSLS_RELATIVE_ERROR, 1.0e-05,
for (i=0; i<=model[0]+model[1]; i++)
printf("%d\t\t%lf\n", i, parameters_user[i]);
printf("\nNumber of outliers: %d\n\n", num_outliers);
printf("Outlier statistics:\n");
printf("Time point\tOutlier type\n");
for (i=0; i<num_outliers; i++)
printf("%d\t\t%d\n", outlier_stat_user[2*i], outlier_stat_user[2*i+1]);
printf("\nOmega statistics:\n");
printf("Time point\tomega\n");
for (i=0; i<num_outliers; i++)
printf("%d\t%18.6f\n", outlier_stat_user[2*i], omega_user[i]);
printf("RSE:%lf\n", res_sigma);
Output
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |
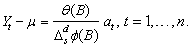
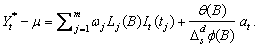
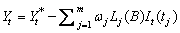 .
. for an additive outlier,
for an additive outlier,