Performs Friedman's test for a randomized complete block design.
Synopsis
#include <imsls.h>
float
imsls_f_friedmans_test (int
n_blocks,
int
n_treatments,
float
y[], ..., 0)
The type double function is imsls_d_friedmans_test.
Required Arguments
int n_blocks
(Input)
Number of blocks.
int
n_treatments (Input)
Number of
treatments.
float y[]
(Input)
Array of size
n_blocks * n_treatments containing the observations. The first
n_treatments
positions of y[]
contain the observations on treatments 1, 2, …, n_treatments in the
first block. The second n_treatments positions
contain the observations in the second block, etc., and so on.
Return Value
The Chi-squared approximation of the asymptotic p-value for
Friedman's
two-sided test statistic.
Synopsis with Optional Arguments
#include <imsls.h>
float
imsls_f_friedmans_test (int
n_blocks, int
n_treatments,
float
y[],
IMSLS_FUZZ, float
fuzz,
IMSLS_ALPHA, float
alpha,
IMSLS_STAT, float
**stat,
IMSLS_STAT_USER, float
stat[],
IMSLS_SUM_RANK, float
**sum_ranks,
IMSLS_SUM_RANK_USER,float
sum_rank[]
IMSLS_DIFFERENCE, float *difference,
0)
Optional Arguments
IMSLS_FUZZ,
float
fuzz (Input)
Constant used to determine ties. In
the ordered observations, if
|y[i] –y[i + 1]|
is less than or equal to fuzz, then y[i] and y[i + 1] are
said to be tied.
Default value is 0.0.
IMSLS_ALPHA, float alpha
(Input)
Critical level for multiple comparisons. alpha should be
between 0 and 1 exclusive. Default value is 0.05.
IMSLS_STAT, float **stat
(Output)
Address of a pointer to an array of length 6 containing
the Friedman statistics. Probabilities reported are computed under the
appropriate null hypothesis.
I stat(I)
0 Friedman two-sided test statistic.
1 Approximate F value for stat[0].
2 Page test statistic for testing the ordered alternative that the median of treatment i is less than or equal to the median of treatment i + 1, with strict inequality holding for some i.
3 Asymptotic p-value for stat[0]. Chi-squared approximation.
4. Asymptotic p-value for stat[1]. F approximation.
5. Asymptotic p-value for stat[2]. Normal approximation.
IMSLS_STAT_USER, float stat[]
(Output)
Storage for array stat is provided by
the user. See IMSLS_STAT.
IMSLS_SUM_RANK,
float
**sum_rank, (Output)
Address of a pointer to an array of length n_treatments
containing the sum of the ranks of each treatment.
IMSLS_SUM_RANK_USER,
float
sum_rank[],
(Output)
Storage for
array sum_rank
is provided by the user.
See IMSLS_SUM_RANK.
IMSLS_DIFFERENCE,
float
*difference, (Output
Minimum absolute
difference in two elements of sum_rank to infer at the alpha level of
significance that the medians of the corresponding treatments are different.
Description
Function imsls_f_friedmans_test may be used to test the hypothesis of equality of treatment effects within each block in a randomized block design. No missing values are allowed. Ties are handled by using the average ranks. The test statistic is the nonparametric analogue of an analysis of variance F test statistic.
The test proceeds by first ranking the observations within each block. Let A denote the sum of the squared ranks, i.e., let
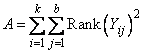
where Rank(Yij) is the rank of the i-th observation within the j-th block, b = NB is the number of blocks, and k = NT is the number of treatments. Let
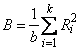
where
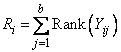
The Friedman test statistic (stat[0]) is given by:
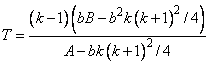
that, under the null hypothesis, has an approximate
chi-squared distribution with
k - 1 degrees of freedom. The asymptotic
probability of obtaining a larger chi-squared random variable is returned in
stat[3].
If the F distribution is used in place of the chi-squared distribution, then the usual oneway analysis of variance F-statistic computed on the ranks is used. This statistic, reported in stat[1], is given by

and asymptotically follows an F distribution with (k - 1) and (b - 1)(k - 1) degrees of freedom under the null hypothesis. stat[4] is the asymptotic probability of obtaining a larger F random variable. (If A = B, stat[0] and stat[1] are set to machine infinity, and the significance levels are reported as k!/(k!)b, unless this computation would cause underflow, in which case the significance levels are reported as zero.) Iman and Davenport (1980) discuss the relative advantages of the chi-squared and F approximations. In general, the F approximation is considered best.
The Friedman T statistic is related both to the Kendall coefficient of concordance and to the Spearman rank correlation coefficient. See Conover (1980) for a discussion of the relationships.
If, at the a = alpha level of significance, the Friedman test results in rejection of the null hypothesis, then an asymptotic test that treatments i and j are different is given by: reject H0 if |Ri - Rj| > D, where
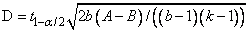
where t has (b - 1)(k - 1) degrees of freedom. Page's statistic (stat[2]) is used to test the same null hypothesis as the Friedman test but is sensitive to a monotonic increasing alternative. The Page test statistic is given by
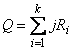
It is largest (and thus most likely to reject) when the Ri are monotonically increasing.
Assumptions
The assumptions in the Friedman test are as follows:
1. The k-vectors of responses within each of the b blocks are mutually independent (i.e., the results within one block have no effect on the results within another block).
2. Within each block, the observations may be ranked.
The hypothesis tested is that each ranking of the random variables within each block is equally likely. The alternative is that at least one of the treatments tends to have larger values than one or more of the other treatments. The Friedman test is a test for the equality of treatment means or medians.
Example
The following example is taken from Bradley (1968), page
127, and tests the hypothesis that 4 drugs have the same effects upon a person's
visual acuity.
Five subjects were used.
#include <imsls.h>
#include <stdio.h>
int main()
{
int n_blocks = 5, n_treatments = 4;
float y[20] = {.39,.55,.33,.41,.21,.28,.19,.16,.73,.69,.64,
.62,.41,.57,.28,.35,.65,.57,.53,.60};
float fuzz = .001, alpha = .05;
float pvalue, *sum_rank, stat[6], difference;
pvalue = imsls_f_friedmans_test(n_blocks, n_treatments, y,
IMSLS_SUM_RANK, &sum_rank,
IMSLS_STAT_USER, stat,
IMSLS_DIFFERENCE, &difference,
0);
printf("\np value for Friedman's T = %f\n\n", pvalue);
printf("Friedman's T = ............ %4.2f\n", stat[0]);
printf("Friedman's F = ............ %4.2f\n", stat[1]);
printf("Page Test = ............... %5.2f\n", stat[2]);
printf("Prob Friedman's T = ....... %7.5f\n", stat[3]);
printf("Prob Friedman's F = ....... %7.5f\n", stat[4]);
printf("Prob Page Test = .......... %7.5f\n", stat[5]);
printf("Sum of Ranks = ............ %4.2f %4.2f %4.2f %4.2f\n",
sum_rank[0], sum_rank[1], sum_rank[2], sum_rank[3]);
printf("difference = .............. %7.5f\n", difference);
}
Output
P value for Friedman's T = 0.040566
p value for Friedman's T = 0.040566
Friedman's T = ............ 8.28
Friedman's F = ............ 4.93
Page Test = ............... 111.00
Prob Friedman's T = ....... 0.04057
Prob Friedman's F = ....... 0.01859
Prob Page Test = .......... 0.98495
Sum of Ranks = ............ 16.00 17.00 7.00 10.00
difference = .............. 6.656388
The Friedman null hypothesis is rejected at the a = .05 while the Page null hypothesis is not. (A Page test with a monotonic decreasing alternative would be rejected, however.) Using sum_rank and difference, one can conclude that treatment 3 is different from treatments 1 and 2, and that treatment 4 is different from treatment 2, all at the a = .05 level of significance.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |