Evaluates the real gamma function.

Synopsis

#include <imsls.h>

float imsls_f_gamma (float x)

The type double procedure is imsls_d_gamma.

Required Arguments

float x   (Input)
Point at which the gamma function is to be evaluated.

Return Value

The value of the gamma function Γ(x).

Description

The gamma function, Γ(x), is defined to be

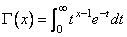
For x < 0, the above definition is extended by analytic continuation.

The gamma function is not defined for integers less than or equal to zero. It underflows for x << 0 and overflows for large x. It also overflows for values near negative integers.

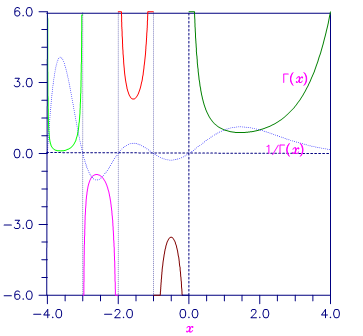
Figure 15- 2   Plot of Γ(x) and 1/Γ(x)

Alert Errors

IMSLS_SMALL_ARG_UNDERFLOW              The argument x must be large enough that Γ(x) does not underflow. The underflow limit occurs first for argu­ments close to large negative half integers. Even though other arguments away from these half integers may yield machine-representable values of Γ(x), such argu­ments are considered illegal.

Warning Errors

IMSLS_NEAR_NEG_INT_WARN                  The result is accurate to less than one-half precision because x is too close to a negative integer.

Example

In this example, Γ(1.5) is computed and printed.

#include <stdio.h>

#include <imsls.h>

 

int main()

{

    float       x = 1.5;

    float       ans;

   

    ans = imsls_f_gamma(x);

    printf("Gamma(%f) = %f\n", x, ans);

}

Output

Gamma(1.500000) = 0.886227

Fatal Errors

IMSLS_ZERO_ARG_OVERFLOW                  The argument for the gamma function is too close to zero.

IMSLS_NEAR_NEG_INT_FATAL                The argument for the function is too close to a negative integer.

IMSLS_LARGE_ARG_OVERFLOW                The function overflows because x is too large.

IMSLS_CANNOT_FIND_XMIN                     The algorithm used to find xmin failed. This error should never occur.

IMSLS_CANNOT_FIND_XMAX                     The algorithm used to find xmax failed. This error should never occur.

Visual Numerics, Inc. Visual Numerics - Developers of IMSL and PV-WAVE http://www.vni.com/ PHONE: 713.784.3131 FAX:713.781.9260