Computes the sample partial autocorrelation function of a stationary time series.
Synopsis
#include <imsls.h>
float *imsls_f_partial_autocorrelation (int lagmax, int cf[], …, 0)
The type double function is imsls_d_partial_autocorrelation.
Required Arguments
int lagmax
(Input)
Maximum lag of partial autocorrelations to be computed.
float cf[]
(Input)
Array of length lagmax + 1 containing the
autocorrelations of the time series x.
Return Value
Pointer to an array of length lagmax containing the partial autocorrelations of the time series x.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_partial_autocorrelation (int
lagmax,
float
cf[],
IMSLS_RETURN_USER, float
partial_autocorrelations[],
0)
Optional Arguments
IMSLS_RETURN_USER, float
partial_autocorrelations[] (Output)
If specified, the
partial autocorrelations are stored in an array of length lagmax provided by the
user.
Description
Function imsls_f_partial_autocorrelation estimates the partial autocorrelations of a stationary time series given the K = lagmax sample autocorrelations
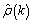
for k = 0, 1, …, K. Consider the AR(k) process defined by
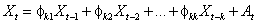
where fkj denotes the j-th coefficient in the process. The set of estimates

for k = 1, …, K is the sample partial autocorrelation function. The autoregressive parameters
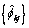
for j = 1, …, k are approximated by
Yule-Walker estimates for successive AR(k) models where
k = 1,
…, K. Based on the sample Yule-Walker equations
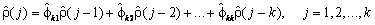
a recursive relationship for k = 1, …, K was developed by Durbin (1960). The equations are given by
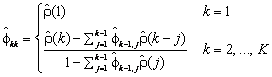
and
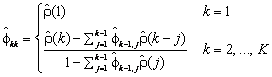
This procedure is sensitive to rounding error and should not be used if the parameters are near the nonstationarity boundary. A possible alternative would be to estimate {fkk} for successive AR(k) models using least or maximum likelihood. Based on the hypothesis that the true process is AR(p), Box and Jenkins (1976, page 65) note
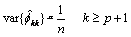
See Box and Jenkins (1976, pages 82–84) for more information concerning the partial autocorrelation function.
Example
Consider the Wolfer Sunspot Data (Anderson 1971, page 660) consisting of the number of sunspots observed each year from 1749 through 1924. The data set for this example consists of the number of sunspots observed from 1770 through 1869. Routine imsls_f_partial_autocorrelation is used to compute the estimated partial autocorrelations.
#include <imsls.h>
#include <stdio.h>
int main()
{
float *partial=NULL, data[176][2], x[100];
int i, nobs = 100, lagmax = 20;
float *ac;
imsls_f_data_sets(2, IMSLS_RETURN_USER, data, 0);
for (i=0;i<nobs;i++) x[i] = data[21+i][1];
ac = imsls_f_autocorrelation(100, x, lagmax, 0);
partial = imsls_f_partial_autocorrelation(lagmax, ac, 0);
imsls_f_write_matrix("Lag PACF", 20, 1, partial, 0);
}
Output
Lag PACF
1 0.806
2 -0.635
3 0.078
4 -0.059
5 -0.001
6 0.172
7 0.109
8 0.110
9 0.079
10 0.079
11 0.069
12 -0.038
13 0.081
14 0.033
15 -0.035
16 -0.131
17 -0.155
18 -0.119
19 -0.016
20 -0.004
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |