Generates pseudorandom numbers from a multivariate distribution determined from a given sample.
Synopsis
#include <imsls.h>
float *imsls_f_random_mvar_from_data (int n_random, int ndim, int nsamp, float x[], int nn, ..., 0)
The type double function is imsls_d_random_mvar_from_data.
Required Arguments
int n_random
(Input)
Number of random multivariate vectors to
generate.
int ndim
(Input)
The length of the multivariate vectors,
that is, the number of dimensions.
int nsamp
(Input)
Number of given data points from the
distribution to be simulated.
float x[]
(Input)
Array of size nsamp ´
ndim matrix containing the given
sample.
int nn
(Input)
Number of nearest neighbors of the
randomly selected point in x that are used to form the output point in the
result.
Return Value
n_random ´ ndim matrix containing the random multivariate vectors in its rows. To release this space, use free.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_random_mvar_from_data (int
n_random,
int ndim,
int nsamp,
float x[],
int nn,
IMSLS_X_COL_DIM, int
x_col_dim,
IMSLS_RETURN_USER, float
r[],
0)
Optional Arguments
IMSLS_X_COL_DIM, int x_col_dim
(Input)
Column dimension of the matrix
x.
Default:
x_col_dim = ndim
IMSLS_RETURN_USER, float r[]
(Output)
User-supplied array of length n_random ´ ndim containing
the random correlation
matrix.
Description
Given a sample of size n (= nsamp) of observations of a k-variate random variable, imsls_f_random_mvar_from_data generates a pseudorandom sample with approximately the same moments as the given sample. The sample obtained is essentially the same as if sampling from a Gaussian kernel estimate of the sample density. (See Thompson 1989.) Routine imsls_f_random_mvar_from_data uses methods described by Taylor and Thompson (1986).
Assume that the (vector-valued) observations xi are in the rows of x. An observation, xj, is chosen randomly; its nearest m (= nn) neighbors,
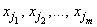
are determined; and the mean
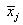
of those nearest neighbors is calculated. Next, a random sample
u1, u2, ¼, um is generated from a uniform distribution with lower bound
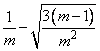
and upper bound
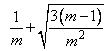
The random variate delivered is
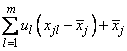
The process is then repeated until n_random such simulated variates are generated and stored in the rows of the result.
Example
In this example, imsls_f_random_mvar_from_data is used to generate 5 pseudorandom vectors of length 4 using the initial and final systolic pressure and the initial and final diastolic pressure from Data Set A in Afifi and Azen (1979) as the fixed sample from the population to be modeled. (Values of these four variables are in the seventh, tenth, twenty-first, and twenty-fourth columns of data set number nine in routine imsls_f_data_sets, Chapter 15, “Utilities”.)
#include <stdio.h>
#include <imsls.h>
int main()
{
int i, nrrow, nrcol, nr = 5, k=4, nsamp = 113, nn = 5;
float x[113][4], rdata[113][34], *r;
imsls_random_seed_set(123457);
imsls_f_data_sets(9,
IMSLS_N_OBSERVATIONS, &nrrow,
IMSLS_N_VARIABLES, &nrcol,
IMSLS_RETURN_USER, rdata,
0);
for (i=0;i<nrrow;i++) x[i][0] = rdata[i][6];
for (i=0;i<nrrow;i++) x[i][1] = rdata[i][9];
for (i=0;i<nrrow;i++) x[i][2] = rdata[i][20];
for (i=0;i<nrrow;i++) x[i][3] = rdata[i][23];
r = imsls_f_random_mvar_from_data(nr, k, nsamp, x, nn, 0);
imsls_f_write_matrix("Random variates", 5, 4, r, 0);
}
Output
Random variates
1 2 3 4
1 162.8 90.5 153.7 104.9
2 153.4 78.3 176.7 85.2
3 93.7 48.2 153.5 71.4
4 101.8 54.2 113.1 56.3
5 91.7 58.8 48.4 28.1
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |