Fits a multivariate linear regression model using least squares.
Synopsis
#include <imsls.h>
float *imsls_f_regression (int n_rows, int n_independent, float x[], float y[], ..., 0)
The type double function is imsls_d_regression.
Required Arguments
int n_rows
(Input)
Number of rows in x.
int
n_independent (Input)
Number of independent (explanatory)
variables.
float x[]
(Input)
Array of size n_rows ื n_independent
containing the independent (explanatory) variables(s). The i-th column of
x contains the i-th independent variable.
float y[]
(Input)
Array of size n_rows ื n_dependent containing
the dependent (response) variables(s). The i-th column of y contains the
i-th dependent variable. See optional argument IMSLS_N_DEPENDENT to
set the value of n_dependent.
Return Value
If the optional argument IMSLS_NO_INTERCEPT is not used, regression returns a pointer to an array of length n_dependent ื (n_independent + 1) containing a least-squares solution for the regression coefficients. The estimated intercept is the initial component of each row, where the i-th row contains the regression coefficients for the i-th dependent variable.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_regresssion (int
n_rows,
int
n_independent,
float
x[],
float
y[],
IMSLS_X_COL_DIM, int
x_col_dim,
IMSLS_Y_COL_DIM, int
y_col_dim,
IMSLS_N_DEPENDENT, int
n_dependent,
IMSLS_X_INDICES, int
indind[],
int
inddep[],
int
ifrq,
int iwt,
IMSLS_IDO, int ido,
IMSLS_ROWS_ADD, or
IMSLS_ROWS_DELETE,
IMSLS_INTERCEPT, or
IMSLS_NO_INTERCEPT,
IMSLS_TOLERANCE, float
tolerance,
IMSLS_RANK, int
*rank,
IMSLS_COEF_COVARIANCES, float
**coef_covariances,
IMSLS_COEF_COVARIANCES_USER, float
coef_covariances[],
IMSLS_COV_COL_DIM, int
cov_col_dim,
IMSLS_X_MEAN, float
**x_mean,
IMSLS_X_MEAN_USER, float
x_mean[],
IMSLS_RESIDUAL, float
**residual,
IMSLS_RESIDUAL_USER, float
residual[],
IMSLS_ANOVA_TABLE, float
**anova_table,
IMSLS_ANOVA_TABLE_USER, float
anova_table[],
IMSLS_FREQUENCIES, float
frequencies[],
IMSLS_SCPE, float
**scpe[],
IMSLS_SCPE_USER, float
scpe_user[],
IMSLS_WEIGHTS, float
weights[],
IMSLS_REGRESSION_INFO, Imsls_f_regression **regression_info,
IMSLS_RETURN_USER, float
coefficients[],
0)
Optional Arguments
IMSLS_X_COL_DIM, int x_col_dim
(Input)
Column dimension of x.
Default:
x_col_dim = n_independent
IMSLS_Y_COL_DIM, int y_col_dim
(Input)
Column dimension of y.
Default:
y_col_dim = n_dependent
IMSLS_N_DEPENDENT, int
n_dependent (Input)
Number of dependent variables. Input
matrix y must be
declared of size n_rows by n_dependent, where
column i of y contains the
i-th dependent variable.
Default: n_dependent = 1
IMSLS_X_INDICES, int indind[], int inddep, int ifrq, int iwt
(Input)
This argument allows an alternative method for data specification.
Data (independent, dependent, frequencies, and weights) is all stored in the
data matrix x.
Argument y, and
keywords IMSLS_FREQUENCIES and
IMSLS_WEIGHTS
are ignored.
Each of the four arguments contains indices indicating column numbers of x in which particular types of data are stored. Columns are numbered 0 x_col_dim − 1.
Parameter indind contains the indices of the independent variables..
Parameter inddep contains the indices of the dependent variables.
Parameters ifrq and iwt contain the column numbers of x in which the frequencies and weights, respectively, are stored. Set ifrq = −1 if there will be no column for frequencies. Set iwt = −1 if there will be no column for weights. Weights are rounded to the nearest integer. Negative weights are not allowed.
Note that required input argument y is not referenced, and can be declared a vector of length 1.
IMSLS_IDO, int ido
(Input)
Processing option.
|
Ido |
Action |
|
0 |
This is the only invocation; all the data are input at once. (Default) |
|
1 |
This is the first invocation with this data; additional calls will be made. Initialization and updating for the n_rows observations of x will be performed. |
|
2 |
This is an intermediate invocation; updating for the n_rows observations of x will be performed. |
|
3 |
This is the final invocation of this function. Updating for the data in x and wrap-up computations are performed. Workspace is released. No further call to regression with ido greater than 1 should be made without first calling regression with ido = 1 |
Default: ido = 0
IMSLS_ROWS_ADD, or
IMSLS_ROWS_DELETE
By
default (or if IMSLS_ROWS_ADD is
specified), the observations in x are added to the discriminant statistics. If
IMSLS_ROWS_DELETE is
specified, then the observations are deleted.
If ido = 0, these optional arguments are ignored (data is always added if there is only one invocation).
IMSLS_INTERCEPT, or
IMSLS_NO_INTERCEPT
IMSLS_INTERCEPT is the
default where the fitted value for observation i is
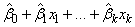
where k = n_independent. If IMSLS_NO_INTERCEPT is specified, the intercept term

is omitted from the model and the return value from regression is a pointer to an array of length n_dependent ื n_independent.
IMSLS_TOLERANCE, float tolerance
(Input)
Tolerance used in determining linear dependence. For regression, tolerance = 100 ื imsls_f_machine(4) is
the default choice. For imsls_d_regression,
tolerance = 100 ื imsls_d_machine(4) is
the default. (See imsls_f_machine Chapter 15 ,
Ultilities.)
IMSLS_RANK, int *rank
(Output)
Rank of the fitted model is returned in *rank.
IMSLS_COEF_COVARIANCES, float
**coef_covariances (Output)
Address of a pointer to the
n_dependent ื m ื m internally
allocated array containing the estimated variances and covariances of the
estimated regression coefficients. Here, m is the number of regression
coefficients in the model. If IMSLS_NO_INTERCEPT is
specified, n = n_independent;
otherwise, m = n_independent + 1.
The first m ื m elements contain the matrix for the first dependent variable, the next m ื m elements contain the matrix for the next dependent variable, ... and so on.
IMSLS_COEF_COVARIANCES_USER, float
coef_covariances[] (Output)
Storage for arrays coef_covariances is
provided by the user. See IMSLS_COEF_COVARIANCES.
IMSLS_COV_COL_DIM, int
cov_col_dim (Input)
Column dimension of array coef_covariances.
Default:
cov_col_dim = m,
where m is the number of regression coefficients in the model
IMSLS_X_MEAN, float **x_mean
(Output)
Address of a pointer to the internally allocated array containing
the estimated means of the independent variables.
IMSLS_X_MEAN_USER, float x_mean[]
(Output)
Storage for array x_mean is provided by
the user.
See IMSLS_X_MEAN.
IMSLS_RESIDUAL, float
**residual (Output)
Address of a pointer to the internally
allocated array of size n_rows by n_dependent containing
the residuals. Residuals may not be requested if ido > 0.
IMSLS_RESIDUAL_USER, float
residual[] (Output)
Storage for array residual is provided
by the user.
See IMSLS_RESIDUAL.
IMSLS_ANOVA_TABLE, float
**anova_table (Output)
Address of a pointer to the
internally allocated array of size
15 ื n_dependent
containing the analysis of variance table for each dependent variable. The
i-th column corresponds to the analysis for the i-th dependent
variable.
The analysis of variance statistics are given as follows:
|
Element |
Analysis of Variance Statistics |
|
0 |
degrees of freedom for the model |
|
1 |
degrees of freedom for error |
|
2 |
total (corrected) degrees of freedom |
|
3 |
sum of squares for the model |
|
4 |
sum of squares for error |
|
5 |
total (corrected) sum of squares |
|
6 |
model mean square |
|
7 |
error mean square |
|
8 |
overall F-statistic |
|
9 |
p-value |
|
10 |
R2 (in percent) |
|
11 |
adjusted R2 (in percent) |
|
12 |
estimate of the standard deviation |
|
13 |
overall mean of y |
|
14 |
coefficient of variation (in percent) |
The anova statistics may not be requested if ido > 0.
IMSLS_ANOVA_TABLE_USER, float
anova_table[] (Output)
Storage for array anova_table is
provided by the user. See IMSLS_ANOVA_TABLE.
IMSLS_SCPE, float **scpe
(Output)
The address of a pointer to an internally allocated array of size
n_dependent x n_dependent containing the
error (residual) sums of squares and crossproducts. scpe [m][n] contains the sum of
crossproducts for the m-th and n-th dependent
variables.
IMSLS_SCPE_USER, float scpe[]
(Output)
Storage for array scpe is provided by
the user. See IMSLS_SCPE.
IMSLS_FREQUENCIES, float
frequencies[] (Input)
Array of length n_rows containing the
frequency for each observation.
Default: frequencies[] =
1
IMSLS_WEIGHTS, float weights[]
(Input)
Array of length n_rows containing the
weight for each observation.
Default: weights[] = 1
IMSLS_REGRESSION_INFO,
Imsls_f_regression
**regression_info (Output)
Address of the pointer to an
internally allocated structure of type Imsls_f_regression containing
information about the regression fit. This structure is required as input for
functions imsls_f_regression_prediction
and imsls_f_regression_summary.
IMSLS_RETURN_USER, float
coefficients[] (Output)
If specified, the least-squares
solution for the regression coefficients is stored in array coefficients
provided by the user. If IMSLS_NO_INTERCEPT is
specified, the array requires
n_dependent ื n units of
memory, where n = n_independent;
otherwise, n = n_independent + 1.
Description
Function imsls_f_regression fits a multivariate multiple linear regression model with or without an intercept. The multiple linear regression model is
yi = β0 + β1xi1 + β2xi2 + + βkxik + ɛi i = 1, 2, , n
where the observed values of the yi's are the responses or values of the dependent variable; the xi1's, xi2's, , xik's are the settings of the k (input in n_independent) independent variables; β0, β1, , βk are the regression coefficients whose estimated values are to be output by imsls_f_regression; and the ɛi's are independently distributed normal errors each with mean 0 and variance s2. Here, n is the sum of the frequencies for all nonmissing observations, i.e.,
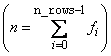
where fi is equal to frequencies[i] if optional argument IMSLS_FREQUENCIES is specified and equal to 1.0 otherwise. Note that by default, β0 is included in the model.
More generally, imsls_f_regression fits a multivariate regression model. See the chapter introduction for a description of the multivariate model.
Function imsls_f_regression computes estimates of the regression coefficients by minimizing the sum of squares of the deviations of the observed response yi from the fitted response
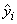
for the n observations. This minimum sum of squares (the error sum of squares) is output as one of the analysis of variance statistics if IMSLS_ANOVA_TABLE (or IMSLS_ANOVA_TABLE_USER) is specified and is computed as follows:
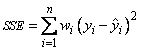
Another analysis of variance statistic is the total sum of squares. By default, the total sum of squares is the sum of squares of the deviations of yi from its mean
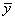
the so-called corrected total sum of squares. This statistic is computed as follows:
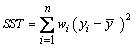
When IMSLS_NO_INTERCEPT is specified, the total sum of squares is the sum of squares of yi, the so-called uncorrected total sum of squares. This is computed as follows:
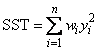
See Draper and Smith (1981) for a good general treatment of the multiple linear regression model, its analysis, and many examples.
In order to compute a least-squares solution, imsls_f_regression performs an orthogonal reduction of the matrix of regressors to upper-triangular form. The reduction is based on one pass through the rows of the augmented matrix (x, y) using fast Givens transformations. (See Golub and Van Loan 1983, pp. 156162; Gentleman 1974.) This method has the advantage that the loss of accuracy resulting from forming the crossproduct matrix used in the normal equations is avoided.
By default, the current means of the dependent and independent variables are used to internally center the data for improved accuracy. Let xi be a column vector containing the j-th row of data for the independent variables. Let xi represent the mean vector for the independent variables given the data for rows 1, 2, , i. The current mean vector is defined as follows:

where the wj's and the fj's are the weights and frequencies. The i-th row of data has
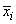
subtracted from it and is multiplied by
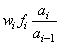
where
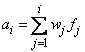
Although a crossproduct matrix is not computed, the validity of this centering operation can be seen from the following formula for the sum of squares and crossproducts matrix:
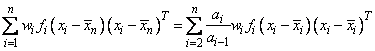
An orthogonal reduction on the centered matrix is computed. When the final computations are performed, the intercept estimate and the first row and column of the estimated covariance matrix of the estimated coefficients are updated (if IMSLS_COEF_COVARIANCES or IMSLS_COEF_COVARIANCES_USER is specified) to reflect the statistics for the original (uncentered) data. This means that the estimate of the intercept is for the uncentered data.
As part of the final computations, imsls_f_regression checks for linearly dependent regressors. In particular, linear dependence of the regressors is declared if any of the following three conditions are satisfied:
A regressor equals 0.
Two or more regressors are constant.
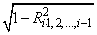
is less than or equal to tolerance. Here,

is the multiple correlation coefficient of the i-th independent variable with the first i 1 independent variables. If no intercept is in the model, the multiple correlation coefficient is computed without adjusting for the mean.
On completion of the final computations, if the i-th regressor is declared to be linearly dependent upon the previous i − 1 regressors, the i-th coefficient estimate and all elements in the i-th row and i-th column of the estimated variance-covariance matrix of the estimated coefficients (if IMSLS_COEF_COVARIANCES or IMSLS_COEF_COVARIANCES_USER is specified) are set to 0. Finally, if a linear dependence is declared, an informational (error) message, code IMSLS_RANK_DEFICIENT, is issued indicating the model is not full rank.
Examples
Example 1
A regression model
yi = β0 + β 1xi1 + β2xi2 + β3xi3 + ɛi i = 1, 2, , 9
is fitted to data taken from Maindonald (1984, pp. 203204).
#include <imsls.h>
#define INTERCEPT 1
#define N_INDEPENDENT 3
#define N_COEFFICIENTS (INTERCEPT + N_INDEPENDENT)
#define N_OBSERVATIONS 9
int main()
{
float *coefficients;
float x[][N_INDEPENDENT] = {7.0, 5.0, 6.0,
2.0,-1.0, 6.0,
7.0, 3.0, 5.0,
-3.0, 1.0, 4.0,
2.0,-1.0, 0.0,
2.0, 1.0, 7.0,
-3.0,-1.0, 3.0,
2.0, 1.0, 1.0,
2.0, 1.0, 4.0};
float y[] = {7.0,-5.0, 6.0, 5.0, 5.0, -2.0, 0.0, 8.0, 3.0};
coefficients = imsls_f_regression(N_OBSERVATIONS, N_INDEPENDENT,
(float *)x, y, 0);
imsls_f_write_matrix("Least-Squares Coefficients", 1, N_COEFFICIENTS,
coefficients,
IMSLS_COL_NUMBER_ZERO,
0);
}
Output
Least-Squares Coefficients
0 1 2 3
7.733 -0.200 2.333 -1.667
Example 2
A weighted least-squares fit is computed using the model
yi = β0 + β1xi1 + β2xi2 + ɛi i = 1, 2, , 4
and weights 1∕i2 discussed by Maindonald (1984, pp. 67−68).
In the example, IMSLS_WEIGHTS is specified. The minimum sum of squares for error in terms of the original untransformed regressors and responses for this weighted regression is
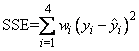
where wi = 1/i2, represented in the C code as array w.
#include <imsls.h>
#include <math.h>
#define N_INDEPENDENT 2
#define N_COEFFICIENTS N_INDEPENDENT + 1
#define N_OBSERVATIONS 4
main()
{
int i;
float *coefficients, w[N_OBSERVATIONS], anova_table[15],
power;
float x[][N_INDEPENDENT] = {
-2.0, 0.0,
-1.0, 2.0,
2.0, 5.0,
7.0, 3.0};
float y[] = {-3.0, 1.0, 2.0, 6.0};
char *anova_row_labels[] = {
"degrees of freedom for regression",
"degrees of freedom for error",
"total (uncorrected) degrees of freedom",
"sum of squares for regression",
"sum of squares for error",
"total (uncorrected) sum of squares",
"regression mean square",
"error mean square", "F-statistic",
"p-value", "R-squared (in percent)",
"adjusted R-squared (in percent)",
"est. standard deviation of model error",
"overall mean of y",
"coefficient of variation (in percent)"};
/* Calculate weights */
power = 0.0;
for (i = 0; i < N_OBSERVATIONS; i++) {
power += 1.0;
w[i] = 1.0 / (power*power);
}
/*Perform analysis */
coefficients = imsls_f_regression(N_OBSERVATIONS, N_INDEPENDENT,
(float *) x, y,
IMSLS_WEIGHTS, w,
IMSLS_ANOVA_TABLE_USER, anova_table,
0);
/* Print results */
imsls_f_write_matrix("Least Squares Coefficients", 1,
N_COEFFICIENTS, coefficients, 0);
imsls_f_write_matrix("* * * Analysis of Variance * * *\n", 15, 1,
anova_table,
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_WRITE_FORMAT, "%10.2f",
0);
}
Output
Least Squares Coefficients
1 2 3
-1.431 0.658 0.748
* * * Analysis of Variance * * *
degrees of freedom for regression 2.00
degrees of freedom for error 1.00
total (uncorrected) degrees of freedom 3.00
sum of squares for regression 7.68
sum of squares for error 1.01
total (uncorrected) sum of squares 8.69
regression mean square 3.84
error mean square 1.01
F-statistic 3.79
p-value 0.34
R-squared (in percent) 88.34
adjusted R-squared (in percent) 65.03
est. standard deviation of model error 1.01
overall mean of y -1.51
coefficient of variation (in percent) -66.55
Example 3
A multivariate regression is performed for a data set with two dependent variables. Also, usage of the keyword IMSLS_X_INDICES is demonstrated. Note that the required input variable y is not referenced and is declared as a pointer to a float.
#include <imsls.h>
#define INTERCEPT 1
#define N_INDEPENDENT 3
#define N_DEPENDENT 2
#define N_COEFFICIENTS (INTERCEPT + N_INDEPENDENT)
#define N_OBSERVATIONS 9
main()
{
float coefficients[N_DEPENDENT*N_COEFFICIENTS];
float *dummy;
float scpe[N_DEPENDENT*N_DEPENDENT];
float anova_table[15*N_DEPENDENT];
static float x[] = { 7.0, 5.0, 6.0, 7.0, 1.0,
2.0,-1.0, 6.0, -5.0, 4.0,
7.0, 3.0, 5.0, 6.0, 10.0,
-3.0, 1.0, 4.0, 5.0, 5.0,
2.0,-1.0, 0.0, 5.0, -2.0,
2.0, 1.0, 7.0, -2.0, 4.0,
-3.0,-1.0, 3.0, 0.0, -6.0,
2.0, 1.0, 1.0, 8.0, 2.0,
2.0, 1.0, 4.0, 3.0, 0.0};
int ifrq = -1, iwt=-1;
static int indind[N_INDEPENDENT] = {0, 1, 2};
static int inddep[N_DEPENDENT] = {3, 4};
char *fmt = "%10.4f";
char *anova_row_labels[] = {
"d.f. regression",
"d.f. error",
"d.f. total (uncorrected)",
"ssr",
"sse",
"sst (uncorrected)",
"msr",
"mse", "F-statistic",
"p-value", "R-squared (in percent)",
"adj. R-squared (in percent)",
"est. s.t.d. of model error",
"overall mean of y",
"coefficient of variation (in percent)"};
imsls_f_regression(N_OBSERVATIONS, N_INDEPENDENT,
(float *) x, dummy,
IMSLS_X_COL_DIM, N_INDEPENDENT+N_DEPENDENT,
IMSLS_N_DEPENDENT, N_DEPENDENT,
IMSLS_X_INDICES, indind, inddep, ifrq, iwt,
IMSLS_SCPE_USER, scpe,
IMSLS_ANOVA_TABLE_USER, anova_table,
IMSLS_RETURN_USER, coefficients,
0);
imsls_f_write_matrix("Least Squares Coefficients", N_DEPENDENT,
N_COEFFICIENTS, coefficients,
IMSLS_COL_NUMBER_ZERO, 0);
imsls_f_write_matrix("SCPE", N_DEPENDENT, N_DEPENDENT, scpe,
IMSLS_WRITE_FORMAT, "%10.4f", 0);
imsls_f_write_matrix("* * * Analysis of Variance * * *\n",
15, N_DEPENDENT,
anova_table,
IMSLS_ROW_LABELS, anova_row_labels,
IMSLS_WRITE_FORMAT, "%10.2f",
0);
}
Output
Least Squares Coefficients
0 1 2 3
1 7.733 -0.200 2.333 -1.667
2 -1.633 0.400 0.167 0.667
SCPE
1 2
1 4.0000 20.0000
2 20.0000 110.0000
* * * Analysis of Variance * * *
1 2
d.f. regression 3.00 3.00
d.f. error 5.00 5.00
d.f. total (uncorre 8.00 8.00
cted)
ssr 152.00 56.00
sse 4.00 110.00
sst (uncorrected) 156.00 166.00
msr 50.67 18.67
mse 0.80 22.00
F-statistic 63.33 0.85
p-value 0.00 0.52
R-squared (in 97.44 33.73
percent)
adj. R-squared 95.90 0.00
(in percent)
est. s.t.d. of 0.89 4.69
model error
overall mean of y 3.00 2.00
coefficient of 29.81 234.52
variation (in
percent)
Warning Errors
IMSLS_RANK_DEFICIENT The model is not full rank. There is not a unique least-squares solution.
Fatal Errors
IMSLS_BAD_IDO_6 ido = #. Initial allocations must be performed by making a call to function regression with ido = 1.
IMSLS_BAD_IDO_7 ido = #. A new analysis may not begin until the previous analysis is terminated by a call to function regression with ido = 3.
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |