Estimates the optimum seasonality parameters for a time series using an autoregressive model, AR(p), to represent the time series.
Synopsis
#include <imsls.h>
float
*imsls_f_seasonal_fit(int
n_obs,
float z[],
int
maxlag,
int
n_differences, int
n_s_initial, int
s_initial[],…,0)
The type double function is imsls_d_seasonal_fit.
Required Arguments
int n_obs
(Input)
Number of observations in the time series.
float z[]
(Input)
An array of length n_obs containing the
time series. No missing values in the series are allowed.
int maxlag (Input)
The
maximum lag allowed when fitting an AR(p) model.
int n_differences
(Input)
The number of differences to perform. Argument n_differences must be
greater than or equal to one.
int n_s_initial
(Input)
The number of rows of the array containing the seasonal
differences.
int s_initial[]
(Input)
Array of dimension n_s_initial by n_differences
containing the seasonal differences to test. All values of s_initial must be
greater than or equal to one.
Return Value
Pointer to an array of length n_obs
or n_obs-n_lost
containing the optimum seasonally adjusted, autoregressive series. The
first n_lost
observations in this series are set to NaN, missing values. The seasonal
adjustment is done by selecting optimum values for 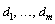 ,
,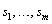 (m=n_differences)
and
(m=n_differences)
and 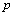 in the AR
model:
in the AR
model:
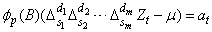 ,
,
where 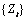 is the original time series,
is the original time series,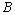 is the backward shift operator
defined by
is the backward shift operator
defined by 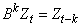 ,
, 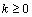 ,
, 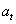 is Gaussian white noise with
is Gaussian white noise with
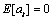 and
and 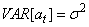 ,
,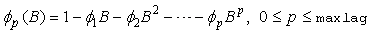 ,
,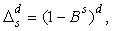 with
with 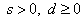 , and
, and 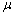 is a centering parameter
for the differenced series.
is a centering parameter
for the differenced series.
NOTE that
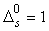 , the identity
operator, i.e.
, the identity
operator, i.e. 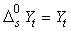 .
.
If an error occurred, then NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_seasonal_fit (int
n_obs, float z[],
int
maxlag,
int
n_differences, int
n_s_initial, int
s_initial[],
IMSLS_RETURN_USER, float
w[],
IMSLS_D_INITIAL, int
n_d_initial, int
d_initial[],
IMSLS_SET_FIRST_TO_NAN, or
IMSLS_EXCLUDE_FIRST,
IMSLS_CENTER, int
n_center,
IMSLS_LOST, int
*n_lost,
IMSLS_BEST_PERIODS,
int
**s,
IMSLS_BEST_PERIODS_USER,
int
s[],
IMSLS_BEST_ORDERS, int
**d,
IMSLS_BEST_ORDERS_USER, int
d[],
IMSLS_AR_ORDER,
int
*p,
IMSLS_AIC,
float
*aic,
0)
Optional Arguments
IMSLS_RETURN_USER,
float w[]
(Output)
An array of length n_obs supplied by the
user to hold the seasonally adjusted series returned by imsls_f_seasonal_fit.
IMSLS_D_INITIAL,
int n_d_initial,
int d_initial[]
(Input)
An array of dimension n_d_initial by n_differences
containing the candidate values for d[], from which the
optimum is being selected. All candidate values in d_initial[] must be
non-negative and
n_d_initial ³ 1.
Default: n_d_initial=1, d_initial an array of
length n_differences filled
with ones.
IMSLS_SET_FIRST_TO_NAN, or
IMSLS_EXCLUDE_FIRST
(Input)
If IMSLS_EXCLUDE_FIRST is
specified, the first n_lost values are
excluded from w
due to differencing. The differenced series w is of length
n_obs–n_lost. If
IMSLS_SET_FIRST_TO_NAN
is specified, the first n_lost observations
are set to NaN
(Not a Number).
Default: IMSLS_SET_FIRST_TO_NAN.
IMSLS_CENTER,
int n_center
(Input)
If supplied, IMSLS_CENTER controls
the method used to center the differenced series. If n_center=0 then the
series is not centered. If n_center=1, the mean
of the series is used to center the data, and if n_center=2, the median
is used.
Default: n_center=1.
IMSLS_LOST, int
*n_lost
(Output)
The number of observations
lost due to differencing the time series. This is also equal to the number
of NaN values that appear in the first n_lost locations of
the returned seasonally adjusted series.
IMSLS_BEST_PERIODS,
int **s
(Output)
Address of a pointer to an
internally allocated array of length m=n_differences
containing the optimum values for the seasonal adjustment parameters 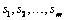 selected from
the list of candidates contained in s_initial[].
selected from
the list of candidates contained in s_initial[].
IMSLS_BEST_PERIODS_USER,
int s[]
(Output)
A user supplied array of
length n_differences for
storage of the array s.
IMSLS_BEST_ORDERS,
int **d
(Output)
Address of a pointer to an
internally allocated array of length m=n_differences
containing the optimum values for the seasonal adjustment parameters 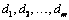 selected from the list of
candidates contained in d_initial[].
selected from the list of
candidates contained in d_initial[].
IMSLS_BEST_ORDERS_USER,
int d[]
(Output)
A user supplied array of
length n_differences for
storage of the array d.
IMSLS_AR_ORDER,
int *p
(Output)
The optimum value for the
autoregressive lag.
IMSLS_AIC,
float *aic
(Output)
Akaike's Information
Criterion (AIC) for the optimum seasonally adjusted model.
Description
Many time series contain seasonal trends and cycles that
can be modeled by first differencing the series. For example, if the
correlation is strong from one period to the next, the series might be
differenced by a lag of 1. Instead of fitting a model to the series
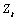 , the model is fitted
to the transformed series:
, the model is fitted
to the transformed series: 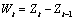 . Higher order lags or differences are warranted if the
series has a cycle every 4 or 13 weeks.
. Higher order lags or differences are warranted if the
series has a cycle every 4 or 13 weeks.
Function imsls_f_seasonal_fit
does not center the original series. If IMSLS_CENTER
is specified with either n_center
=1 or n_center
=2, then the differenced series, 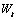 , is centered before determination of minimum AIC and optimum
lag. For every combination of rows in s_initial
and d_initial,
the series
, is centered before determination of minimum AIC and optimum
lag. For every combination of rows in s_initial
and d_initial,
the series 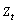 is
converted to the seasonally adjusted series using the following computation
is
converted to the seasonally adjusted series using the following computation
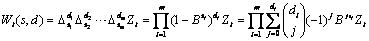 .
.
where 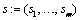 ,
, 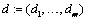 represent specific rows of
arrays s_initial
and d_initial
respectively, and
represent specific rows of
arrays s_initial
and d_initial
respectively, and 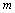 =n_differences.
=n_differences.
This transformation of the series 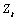 to
to 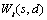 is accomplished using
function imsls_f_difference(). After this
transformation,
is accomplished using
function imsls_f_difference(). After this
transformation,
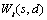
is (optionally) centered and a call is made to imsls_f_auto_uni_ar to automatically determine
the optimum lag for an AR(p) representation for 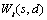 . This procedure is repeated for
every possible combination of rows of s_initial
and d_initial.
The series with the minimum AIC is identified as the optimum representation
and returned.
. This procedure is repeated for
every possible combination of rows of s_initial
and d_initial.
The series with the minimum AIC is identified as the optimum representation
and returned.
Example
Consider the Airline Data (Box, Jenkins and Reinsel 1994, p. 547) consisting of the monthly total number of international airline passengers from January 1949 through December 1960. Function imsls_f_seasonal_fit is used to compute the optimum seasonality representation of the adjusted series
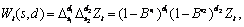
where
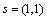
or
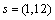
and
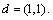
As differenced series with minimum AIC,
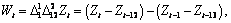
is identified.
#include <imsls.h>
#include <stdlib.h>
#include <stdio.h>
int main()
{
int i;
int maxlag = 10;
int nobs = 144;
int n_differences = 2;
int n_s_initial = 2;
int nlost;
int npar;
float aic;
int s_init[] = { 1, 1,
1, 12};
int *s = NULL;
int *d = NULL;
float *z = NULL;
float *difference = NULL;
z = imsls_f_data_sets(4, 0);
difference = imsls_f_seasonal_fit(nobs, z, maxlag, n_differences,
n_s_initial, s_init,
IMSLS_LOST, &nlost,
IMSLS_BEST_PERIODS, &s,
IMSLS_BEST_ORDERS, &d,
IMSLS_AIC, &aic,
IMSLS_AR_ORDER, &npar,
0);
printf("\nnlost = %d\n", nlost);
printf("s = (%d, %d)\n", s[0], s[1]);
printf("d = (%d, %d)\n", d[0], d[1]);
printf("Order of optimum AR process: %d\n", npar);
printf("aic = %lf\n", aic);
printf("\ni\tz[i]\tdifference[i]\n");
for (i=0; i<nobs; i++)
printf("%d\t%f\t%f\n", i, z[i], difference[i]);
if (s)
{
imsls_free(s);
s = NULL;
}
if (d)
{
imsls_free(d);
d = NULL;
}
if (z)
{
imsls_free(z);
z = NULL;
}
if (difference)
{
imsls_free(difference);
difference = NULL;
}
return;
}
Output
nlost = 13
s = (1, 12)
d = (1, 1)
Order of optimum AR process: 1
aic = 949.780334
i z[i] difference[i]
0 112.000000 NaN
1 118.000000 NaN
2 132.000000 NaN
3 129.000000 NaN
4 121.000000 NaN
5 135.000000 NaN
6 148.000000 NaN
7 148.000000 NaN
8 136.000000 NaN
9 119.000000 NaN
10 104.000000 NaN
11 118.000000 NaN
12 115.000000 NaN
13 126.000000 5.000000
14 141.000000 1.000000
15 135.000000 -3.000000
16 125.000000 -2.000000
17 149.000000 10.000000
18 170.000000 8.000000
19 170.000000 0.000000
20 158.000000 0.000000
21 133.000000 -8.000000
22 114.000000 -4.000000
23 140.000000 12.000000
24 145.000000 8.000000
25 150.000000 -6.000000
26 178.000000 13.000000
27 163.000000 -9.000000
28 172.000000 19.000000
29 178.000000 -18.000000
30 199.000000 0.000000
31 199.000000 0.000000
32 184.000000 -3.000000
33 162.000000 3.000000
34 146.000000 3.000000
35 166.000000 -6.000000
36 171.000000 0.000000
37 180.000000 4.000000
38 193.000000 -15.000000
39 181.000000 3.000000
40 183.000000 -7.000000
41 218.000000 29.000000
42 230.000000 -9.000000
43 242.000000 12.000000
44 209.000000 -18.000000
45 191.000000 4.000000
46 172.000000 -3.000000
47 194.000000 2.000000
48 196.000000 -3.000000
49 196.000000 -9.000000
50 236.000000 27.000000
51 235.000000 11.000000
52 229.000000 -8.000000
53 243.000000 -21.000000
54 264.000000 9.000000
55 272.000000 -4.000000
56 237.000000 -2.000000
57 211.000000 -8.000000
58 180.000000 -12.000000
59 201.000000 -1.000000
60 204.000000 1.000000
61 188.000000 -16.000000
62 235.000000 7.000000
63 227.000000 -7.000000
64 234.000000 13.000000
65 264.000000 16.000000
66 302.000000 17.000000
67 293.000000 -17.000000
68 259.000000 1.000000
69 229.000000 -4.000000
70 203.000000 5.000000
71 229.000000 5.000000
72 242.000000 10.000000
73 233.000000 7.000000
74 267.000000 -13.000000
75 269.000000 10.000000
76 270.000000 -6.000000
77 315.000000 15.000000
78 364.000000 11.000000
79 347.000000 -8.000000
80 312.000000 -1.000000
81 274.000000 -8.000000
82 237.000000 -11.000000
83 278.000000 15.000000
84 284.000000 -7.000000
85 277.000000 2.000000
86 317.000000 6.000000
87 313.000000 -6.000000
88 318.000000 4.000000
89 374.000000 11.000000
90 413.000000 -10.000000
91 405.000000 9.000000
92 355.000000 -15.000000
93 306.000000 -11.000000
94 271.000000 2.000000
95 306.000000 -6.000000
96 315.000000 3.000000
97 301.000000 -7.000000
98 356.000000 15.000000
99 348.000000 -4.000000
100 355.000000 2.000000
101 422.000000 11.000000
102 465.000000 4.000000
103 467.000000 10.000000
104 404.000000 -13.000000
105 347.000000 -8.000000
106 305.000000 -7.000000
107 336.000000 -4.000000
108 340.000000 -5.000000
109 318.000000 -8.000000
110 362.000000 -11.000000
111 348.000000 -6.000000
112 363.000000 8.000000
113 435.000000 5.000000
114 491.000000 13.000000
115 505.000000 12.000000
116 404.000000 -38.000000
117 359.000000 12.000000
118 310.000000 -7.000000
119 337.000000 -4.000000
120 360.000000 19.000000
121 342.000000 4.000000
122 406.000000 20.000000
123 396.000000 4.000000
124 420.000000 9.000000
125 472.000000 -20.000000
126 548.000000 20.000000
127 559.000000 -3.000000
128 463.000000 5.000000
129 407.000000 -11.000000
130 362.000000 4.000000
131 405.000000 16.000000
132 417.000000 -11.000000
133 391.000000 -8.000000
134 419.000000 -36.000000
135 461.000000 52.000000
136 472.000000 -13.000000
137 535.000000 11.000000
138 622.000000 11.000000
139 606.000000 -27.000000
140 508.000000 -2.000000
141 461.000000 9.000000
142 390.000000 -26.000000
143 432.000000 -1.000000
|
Visual Numerics, Inc. PHONE: 713.784.3131 FAX:713.781.9260 |