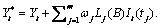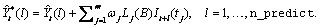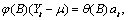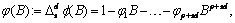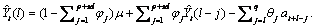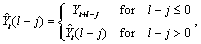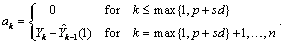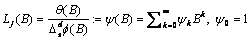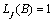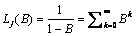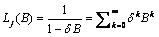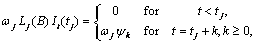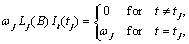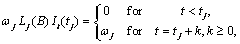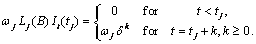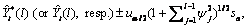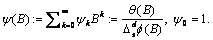ts_outlier_forecast

Chapter 8: Time Series and Forecasting

ts_outlier_forecast

Computes forecasts , their associated probability limits and 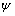weights for an outlier contaminated time series whose underlying outlier free series follows a general seasonal or nonseasonal ARMA model .

Synopsis

#include <imsls.h>

float *imsls_f_ts_outlier_forecast (int n_obs, float series[],
int num_outliers, int outlier_statistics[], float omega[],
float delta, int model[], float parameters[], int n_predict,…,0)

The type double function is imsls_d_ts_outlier_forecast.

Required Arguments

int n_obs (Input)
Number of observations in the time series.

float series[] (Input)
An array of length n_obs by 2 containing the outlier free time series in its first column and the residuals of the series in the second column.

int num_outliers (Input)
Number of detected outliers in the original outlier contaminated series as computed in imsls_f_ts_outlier_identification .

int outlier_statistics[] (Input)
An array of length num_outliers by 2 containing the outlier statistics from imsls_f_ts_outlier_identification . If num_outliers=0, this array is ignored.

float omega[] (Input)
Array of length num_outliers containing the 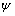weights for the outliers determined in imsls_f_ts_outlier_identification . Ignored, if num_outliers=0.

float delta (Input)
The dynamic dampening effect parameter used in the outlier detection.

int model[] (Input)
Vector of length 4 containing the numbers p, q, s, d of the ARIMA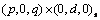 model the outlier free series is following.

float parameters[] (Input)
Vector of length 1+p +q containing the estimated constant, AR and MA parameters as output from imsls_f_ts_outlier_identification .

int n_predict (Input)
Maximum lead time for forecasts. The forecasts are taken at origin t=n_obs, the time point of the last observed value, for lead times 1,2,...,n_predict.

Return Value

Pointer to an array of length n_predict by 3. The first column contains the forecasted values for the original outlier contaminated series. The second column contains the deviations from each forecast for computing confidence probability limits, and the third column contains the 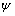weights of the infinite moving average form of the model.

If an error occurred, NULL is returned.

Synopsis with Optional Arguments

#include <imsls.h>

float *imsls_f_ts_outlier_forecast(int n_obs, float series[],
int num_outliers, int outlier_statistics[],
float omega[], float delta, int model[],
float parameters[], int n_predict,
IMSLS_RETURN_USER, float forecast[],
IMSLS_CONFIDENCE, float confidence,
IMSLS_OUT_FREE_FORECAST, float **outfree_forecast,
IMSLS_OUT_FREE_FORECAST_USER, float outfree_forecast[],
0)

Optional Arguments

IMSLS_RETURN_USER, float forecast[] (Output)
An array of length n_predict by 3 supplied by the user containing the forecasts for the original outlier contaminated series in column 1, deviations from each forecast in column 2 and the 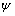weights of the infinite moving average form of the model in column 3.

IMSLS_CONFIDENCE, float confidence (Input)
Value in the exclusive interval (0,100) used to specify the confidence percent probability limits of the forecast.Typical choices for confidence are 90.0, 95.0 and 99.0.
Default: confidence = 95.0

IMSLS_OUT_FREE_FORECAST, float **outfree_forecast (Output)
Address of a pointer to an array of length n_predict by 3 containing the forecasts for the original outlier free series in column 1, deviations from each forecast in column 2 and the 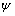weights of the infinite moving average form of the model in column 3.

IMSLS_OUT_FREE_FORECAST_USER, float outfree_forecast[] Output)
Storage for array outfree_forecast is provided by the user. For a description, see IMSLS_OUT_FREE_FORECAST.

Description

Consider the following model for a given outlier contaminated univariate time series :

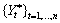For an explanation of the notation, see the “Description ” section for imsls_f_ts_outlier_identification. It follows from the formula above that the Box-Jenkins forecast at origin 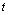for lead time 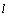, , 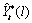can be computed as:

Therefore, computation of the forecasts for 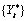is done in two steps:

1. Computation of the forecasts for the outlier free series .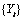

2. Computation of the forecasts for the original series 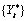by adding the multiple outlier effects to the forecasts for .

Step 1 above:

Since

where

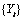the Box-Jenkins forecast at origin 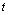for lead time 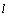, , 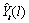can be computed recursively as:

Here,

and

Step 2 above:

The formulas for 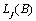for the different types of outliers are as follows:

Innovational outliers (IO)
Additive outliers (AO)
Level shifts (LS)
Temporary changes (TC)

Assuming the outlier occurs at time point 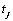, the outlier impact is therefore:

Innovational outliers (IO)
Additive outliers (AO)
Level shifts (LS)
Temporary changes (TC)

From these formulas, the forecasts 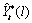can be computed easily.

The 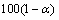percent probability limits for 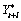and 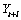are given by

where 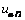is the 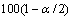percentile of the standard normal distribution, 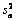is an estimate of the variance 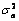of the random shocks (returned from imsls_f_ts_outlier_identification ), and the 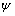weights 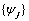are the coefficients in

For a detailed explanation of these concepts, see Chapter 5: “Forecasting”, Box, Jenkins and Reinsel (1994).

Example

This example is a realization of an ARMA(2,1) process described by the model 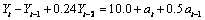, 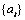a Gaussian white noise process.

Outliers were artificially added to the outlier free series 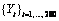at time points 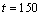(level shift, 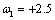) and 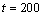(additive outlier, 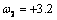), resulting in the outlier contaminated series 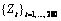. For both series, forecasts were determined for time points 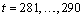and compared with the actual values of the series.

Link to example source

#include <imsls.h>

#include <stdlib.h>

#include <stdio.h>

int main()

{

float time_series[290] ={

41.6699982,41.6699982,42.0752144,42.6123962,43.6161919,42.1932831,

43.1055450,44.3518715,45.3961258,45.0790215,41.8874397,40.2159805,

40.2447319,39.6208458,38.6873589,37.9272423,36.8718872,36.8310852,

37.4524879,37.3440933,37.9861374,40.3810501,41.3464622,42.6495285,

42.6096764,40.3134537,39.7971268,41.5401535,40.7160759,41.0363541,

41.8171883,42.4190292,43.0318832,43.9968109,44.0419617,44.3225212,

44.6082611,43.2199631,42.0419197,41.9679718,42.4926224,43.2091255,

43.2512283,41.2301674,40.1057358,40.4510574,41.5329170,41.5678177,

43.0090141,42.1592140,39.9234505,38.8394127,40.4319878,40.8679352,

41.4551926,41.9756317,43.9878922,46.5736389,45.5939293,42.4487762,

41.5325394,42.8830910,44.5771217,45.8541985,46.8249474,47.5686378,

46.6700745,45.4120026,43.2305107,42.7635345,43.7112923,42.0768661,

41.1835632,40.3352280,37.9761467,35.9550056,36.3212509,36.9925880,

37.2625008,37.0040665,38.5232544,39.4119797,41.8316803,43.7091446,

42.9381447,42.1066780,40.3771248,38.6518707,37.0550499,36.9447708,

38.1017685,39.4727097,39.8670387,39.3820763,38.2180786,37.7543488,

37.7265244,38.0290642,37.5531158,37.4685936,39.8233147,42.0480766,

42.4053535,43.0117416,44.1289330,45.0393829,45.1114540,45.0086479,

44.6560631,45.0278931,46.7830849,48.7649765,47.7991905,46.5339661,

43.3679199,41.6420822,41.2694893,41.5959740,43.5330009,43.3643608,

42.1471291,42.5552788,42.4521446,41.7629128,39.9476891,38.3217010,

40.5318718,42.8811569,44.4796944,44.6887932,43.1670265,41.2226143,

41.8330154,44.3721924,45.2697029,44.4174194,43.5068550,44.9793015,

45.0585403,43.2746620,40.3317070,40.3880501,40.2627106,39.6230278,

41.0305252,40.9262009,40.8326912,41.7084885,42.9038048,45.8650513,

46.5231590,47.9916115,47.8463135,46.5921936,45.8854408,45.9130440,

45.7450371,46.2964249,44.9394569,45.8141251,47.5284042,48.5527802,

48.3950577,47.8753052,45.8880005,45.7086983,44.6174774,43.5567932,

44.5891113,43.1778679,40.9405632,40.6206894,41.3330421,42.2759552,

42.4744949,43.0719833,44.2178459,43.8956337,44.1033440,45.6241455,

45.3724861,44.9167595,45.9180603,46.9077835,46.1666603,46.6013489,

46.6592331,46.7291603,47.1908340,45.9784355,45.1215782,45.6791115,

46.7379875,47.3036957,45.9968834,44.4669495,45.7734680,44.6315041,

42.9911766,46.3842583,43.7214432,43.5276833,41.3946495,39.7013168,

39.1033401,38.5292892,41.0096245,43.4535828,44.6525154,45.5725899,

46.2815285,45.2766647,45.3481712,45.5039482,45.6745682,44.0144806,

42.9305000,43.6785469,42.2500534,40.0007210,40.4477005,41.4432716,

42.0058670,42.9357758,45.6758842,46.8809929,46.8601494,47.0449791,

46.5420647,46.8939934,46.2963371,43.5479164,41.3864059,41.4046364,

42.3037987,43.6223717,45.8602371,47.3016396,46.8632469,45.4651413,

45.6275482,44.9968376,42.7558670,42.0218239,41.9883728,42.2571678,

44.3708687,45.7483635,44.8832512,44.7945862,44.8922577,44.7409401,

45.1726494,45.5686874,45.9946709,47.3151054,48.0654068,46.4817467,

42.8618279,42.4550323,42.5791168,43.4230957,44.7787971,43.8317108,

43.6481781,42.4183960,41.8426285,43.3475227,44.4749908,46.3498306,

47.8599319,46.2449913,43.6044006,42.4563484,41.2715340,39.8492508,

39.9997292,41.4410820,42.9388237,42.5687332,42.6384087,41.7088661,

43.9399033,45.4284401,44.4558411,45.1761856,45.3489113,45.1892662,

46.3754730,45.6082802 };

int n_obs = 280, i;

float *parameters = NULL, *result = NULL, *forecast = NULL;

float *outfree_forecast = NULL, *omega = NULL, *residual = NULL;

float res_sigma, aic;

float delta = 0.7;

float series[560];

int *outlier_stat = NULL;

int num_outliers;

int n_predict = 10;

int model[4];

float forecast_table[40];

model[0] = 2;

model[1] = 1;

model[2] = 1;

model[3] = 0;

result = imsls_f_ts_outlier_identification(n_obs, model,

time_series,

IMSLS_RELATIVE_ERROR, 1.0e-5,

IMSLS_NUM_OUTLIERS, &num_outliers,

IMSLS_RESIDUAL, &residual,

IMSLS_OUTLIER_STATISTICS, &outlier_stat,

IMSLS_OMEGA_WEIGHTS, &omega,

IMSLS_ARMA_PARAM, &parameters,

IMSLS_RESIDUAL_SIGMA, &res_sigma,

IMSLS_AIC, &aic,

0);

printf("\nARMA parameters:\n");

for (i=0; i<=model[0]+model[1]; i++)

printf("%d\t\t%lf\n", i, parameters[i]);

printf("\nNumber of outliers: %d\n\n", num_outliers);

printf("Outlier statistics:\n");

printf("Time point\t\tOutlier type\n");

for (i=0; i<num_outliers; i++)

printf("%d\t\t%d\n", outlier_stat[2*i], outlier_stat[2*i+1]);

printf("\n");

printf("RSE:%lf\n", res_sigma);

printf("AIC:%lf\n", aic);

for (i=0; i<n_obs; i++)

{

series[2*i] = result[i];

series[2*i+1] = residual[i];

}

forecast = imsls_f_ts_outlier_forecast(n_obs, series,

num_outliers, outlier_stat, omega, delta,

model, parameters, n_predict,

IMSLS_OUT_FREE_FORECAST,&outfree_forecast, 0);

for (i=0; i<n_predict; i++)

{

forecast_table[4*i] = time_series[n_obs+i];

forecast_table[4*i+1] = forecast[3*i];

forecast_table[4*i+2] = forecast[3*i+1];

forecast_table[4*i+3] = forecast[3*i+2];

}

imsls_f_write_matrix("\t* * * Forecast Table for outlier"

"contaminated series * * *\nOrig. Series"

"\tforecast\tprob. limits\tpsi weights\n",

n_predict, 4, forecast_table,

IMSLS_WRITE_FORMAT, "%11.4f", 0);

for (i=0; i<n_predict; i++)

{

forecast_table[4*i] = time_series[n_obs+i] - 2.5;

forecast_table[4*i+1] = outfree_forecast[3*i];

forecast_table[4*i+2] = outfree_forecast[3*i+1];

forecast_table[4*i+3] = outfree_forecast[3*i+2];

}

printf("\n");

imsls_f_write_matrix("\t* * * Forecast Table for outlier free"

"series * * *\n\nOutlier free series\tforecast"

"\tprob. limits\tpsi weights\n",

n_predict, 4, forecast_table,

IMSLS_WRITE_FORMAT, "%11.4f", 0);

}

Output

ARMA parameters:

0 8.839014

1 0.948735

2 -0.153870

3 -0.553387

Number of outliers: 2

Outlier statistics:

Time point Outlier type

150 2

200 1

RSE:1.004321

AIC:1323.625977

* * * Forecast Table for outlier contaminated series * * *

Orig. series forecast prob. limits psi weights

1 2 3 4

1 42.6384 42.3178 1.9684 1.5021

2 41.7089 42.7910 3.5521 1.2712

3 43.9399 43.2786 4.3450 0.9749

4 45.4284 43.6684 4.7500 0.7294

5 44.4558 43.9632 4.9622 0.5420

6 45.1762 44.1828 5.0756 0.4019

7 45.3489 44.3459 5.1369 0.2979

8 45.1893 44.4668 5.1703 0.2208

9 46.3755 44.5564 5.1885 0.1637

10 45.6083 44.6228 5.1985 0.1213

* * * Forecast Table for outlier free series * * *

Outlier free series forecast prob. limits psi weights

1 2 3 4

1 40.1384 40.5936 1.9684 1.5021

2 39.2089 41.0668 3.5521 1.2712

3 41.4399 41.5544 4.3450 0.9749

4 42.9284 41.9442 4.7500 0.7294

5 41.9558 42.2389 4.9622 0.5420

6 42.6762 42.4586 5.0756 0.4019

7 42.8489 42.6217 5.1369 0.2979

8 42.6893 42.7426 5.1703 0.2208

9 43.8755 42.8322 5.1885 0.1637

10 43.1083 42.8986 5.1985 0.1213

Visual Numerics, Inc.
Visual Numerics - Developers of IMSL and PV-WAVE
http://www.vni.com/
PHONE: 713.784.3131
FAX:713.781.9260