Solves a nonlinear least-squares problem subject to bounds on the variables using a modified Levenberg-Marquardt algorithm.
Synopsis
#include <imsl.h>
float *imsl_f_bounded_least_squares (void fcn(), int m, int n, int ibtype, float xlb[], float xub[], ..., 0)
The type double function is imsl_d_bounded_least_squares.
Required Arguments
void fcn (int m, int n, float x[],
float f[])
(Input/Output)
User-supplied function to evaluate the function that
defines the least-squares problem where x is a vector of
length n at
which point the function is evaluated, and f is a vector of
length m
containing the function values at point x.
int m
(Input)
Number of functions.
int n
(Input)
Number of variables where n ≤ m.
int ibtype
(Input)
Scalar indicating the types of bounds on the variables.
|
ibtype |
Action |
|
0 |
User will supply all the bounds. |
|
1 |
All variables are nonnegative |
|
2 |
All variables are nonpositive. |
|
3 |
User supplies only the bounds on 1st variable, all other variables will have the same bounds |
float xlb[]
(Input, Output, or Input/Output)
Array with n components
containing the lower bounds on the variables. (Input, if ibtype = 0;
output, if ibtype = 1
or 2; Input/Output, if ibtype = 3)
If there is no lower bound on a variable, then the corresponding xlb value should be set to −106.
float xub[]
(Input, Output, or Input/Output)
Array with n components
containing the upper bounds on the variables. (Input, if ibtype = 0;
output, if ibtype 1 or 2;
Input/Output, if ibtype = 3)
If there is no upper bound on a variable, then the corresponding xub value should be set to 106.
Return Value
A pointer to the solution x of the nonlinear least-squares problem. To release this space, use imsl_free. If no solution can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_bounded_least_squares (void fcn(), int m, int n, int ibtype, float xlb[], float xub[],
IMSL_XGUESS, float xguess[],
IMSL_JACOBIAN, void jacobian(),
IMSL_XSCALE, float xscale[],
IMSL_FSCALE, float fscale[],
IMSL_GRAD_TOL, float grad_tol,
IMSL_STEP_TOL, float step_tol,
IMSL_REL_FCN_TOL, float rfcn_tol,
IMSL_ABS_FCN_TOL, float afcn_tol,
IMSL_MAX_STEP, float max_step,
IMSL_INIT_TRUST_REGION, float trust_region,
IMSL_GOOD_DIGIT, int ndigit,
IMSL_MAX_ITN, int max_itn,
IMSL_MAX_FCN, int max_fcn,
IMSL_MAX_JACOBIAN, int max_jacobian,
IMSL_INTERN_SCALE,
IMSL_RETURN_USER, float x[],
IMSL_FVEC, float **fvec,
IMSL_FVEC_USER, float fvec[],
IMSL_FJAC, float **fjac,
IMSL_FJAC_USER, float fjac[],
IMSL_FJAC_COL_DIM, int fjac_col_dim,
IMSL_FCN_W_DATA, void fcn(), void *data,
IMSL_JACOBIAN_W_DATA, void jacobian(), void *data,
0)
Optional Arguments
IMSL_XGUESS, float xguess[]
(Input)
Array with n components
containing an initial guess.
Default: xguess = 0
IMSL_JACOBIAN, void jacobian (int m, int n, float x[], float fjac[], int fjac_col_dim)
(Input)
User-supplied function to compute the Jacobian where x is a vector of
length n at
which point the Jacobian is evaluated, fjac is the computed
m × n
Jacobian at the point x, and fjac_col_dim is the
column dimension of fjac. Note that each
derivative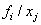 
should be returned in fjac[(i−1)*fjac_col_dim+j−1].
IMSL_XSCALE, float xscale[]
(Input)
Array with n components
containing the scaling vector for the variables. Argument xscale is used mainly
in scaling the gradient and the distance between two points. See keywords IMSL_GRAD_TOL and
IMSL_STEP_TOL
for more details.
Default: xscale[] = 1
IMSL_FSCALE, float fscale[]
(Input)
Array with m components
containing the diagonal scaling matrix for the functions. The i-th
component of fscale is a positive
scalar specifying the reciprocal magnitude of the i-th component function
of the problem.
Default: fscale[] = 1
IMSL_GRAD_TOL, float grad_tol
(Input)
Scaled gradient tolerance. The i-th component of the scaled
gradient at x is
calculated as
where g = ∇ F(x), s = xscale, and
Default: grad_tol =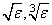 
in double where ɛ is the machine
precision
IMSL_STEP_TOL, float step_tol
(Input)
Scaled step tolerance. The i-th component of the scaled step
between two points x, and y, is computed as
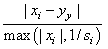
where s = xscale.
Default:
step_tol = ɛ2/3, where
ɛ is the
machine precision
IMSL_REL_FCN_TOL, float rfcn_tol
(Input)
Relative function tolerance.
Default: rfcn_tol = max(10-10, ɛ2/3),
max(10-20, ɛ2/3) in double,
where ɛ is
the machine precision
IMSL_ABS_FCN_TOL, float afcn_tol
(Input)
Absolute function tolerance.
Default: afcn_tol = max(10-20, ɛ2), max(10-40, ɛ2) in double,
where ɛ is
the machine precision
IMSL_MAX_STEP, float max_step
(Input)
Maximum allowable step size.
Default: max_step = 1000 max(ɛ1, ɛ2), where
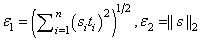
for s = xscale and t = xguess.
IMSL_INIT_TRUST_REGION, float trust_region
(Input)
Size of initial trust region radius. The default is based on the
initial scaled Cauchy step.
IMSL_GOOD_DIGIT, int ndigit
(Input)
Number of good digits in the function.
Default: machine
dependent
IMSL_MAX_ITN, int max_itn
(Input)
Maximum number of iterations.
Default: max_itn = 100
IMSL_MAX_FCN, int max_fcn
(Input)
Maximum number of function evaluations.
Default: max_fcn = 400
IMSL_MAX_JACOBIAN, int max_jacobian
(Input)
Maximum number of Jacobian evaluations.
Default: max_jacobian = 400
IMSL_INTERN_SCALE
Internal variable scaling option. With
this option, the values for xscale are set
internally.
IMSL_RETURN_USER, float x[]
(Output)
Array with n components
containing the computed solution.
IMSL_FVEC, float **fvec
(Output)
The address of a pointer to a real array of length m containing the
residuals at the approximate solution. On return, the necessary space is
allocated by imsl_f_bounded_least_squares.
Typically, float *fvec is declared, and
&fvec is
used as an argument.
IMSL_FVEC_USER, float fvec[]
(Output)
A user-allocated array of size m containing the
residuals at the approximate solution.
IMSL_FJAC,
float **fjac
(Output)
The address of a pointer to an array of size
m × n containing the Jacobian at the approximate
solution. On return, the necessary space is allocated by imsl_f_bounded_least_squares.
Typically, float *fjac is declared, and
&fjac is
used as an argument.
IMSL_FJAC_USER, float fjac[]
(Output)
A user-allocated array of size m × n
containing the Jacobian at the approximate solution.
IMSL_FJAC_COL_DIM, int fjac_col_dim
(Input)
The column dimension of fjac.
Default:
fjac_col_dim = n
IMSL_FCN_W_DATA, void fcn (int m, int n, float x[],
float f[], void *data),
void *data,
(Input)
User-supplied function to evaluate the function that defines the
least-squares problem, which also accepts a pointer to data that is supplied by
the user. data
is a pointer to the data to be passed to the user-supplied function. See the
Introduction, Passing Data
to User-Supplied Functions at the beginning of this manual for more
details.
IMSL_JACOBIAN_W_DATA, void jacobian (int m, int n, float x[], float fjac[], int fjac_col_dim,
void *data),
void *data,
(Input)
User-supplied function to compute the Jacobian, which also accepts a
pointer to data that is supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
Description
The function imsl_f_bounded_least_squares uses a modified Levenberg-Marquardt method and an active set strategy to solve nonlinear least-squares problems subject to simple bounds on the variables. The problem is stated as follows:
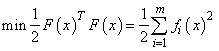
subject to l ≤ x ≤ u
where m ≥ n, F : Rn → Rm, and fi(x) is the i-th component function of F(x). From a given starting point, an active set IA, which contains the indices of the variables at their bounds, is built. A variable is called a “free variable” if it is not in the active set. The routine then computes the search direction for the free variables according to the formula
d = −(JTJ + μ I)-1 JTF
where μ is the Levenberg-Marquardt parameter, F = F(x), and J is the Jacobian with respect to the free variables. The search direction for the variables in IA is set to zero. The trust region approach discussed by Dennis and Schnabel (1983) is used to find the new point. Finally, the optimality conditions are checked. The conditions are
||g (xi)|| ≤ ε, li < xi < ui
g (xi) < 0, xi = ui
g (xi) >0, xi = li
where ε is a gradient tolerance. This process is repeated until the optimality criterion is achieved.
The active set is changed only when a free variable hits its bounds during an iteration or the optimality condition is met for the free variables but not for all variables in IA, the active set. In the latter case, a variable that violates the optimality condition will be dropped out of IA. For more detail on the Levenberg-Marquardt method, see Levenberg (1944) or Marquardt (1963). For more detail on the active set strategy, see Gill and Murray (1976).
Since a finite-difference method is used to estimate the Jacobian for some single-precision calculations, an inaccurate estimate of the Jacobian may cause the algorithm to terminate at a noncritical point. In such cases, high-precision arithmetic is recommended. Also, whenever the exact Jacobian can be easily provided, the option IMSL_JACOBIAN should be used.
On some platforms, imsl_f_bounded_least_squares can evaluate the user-supplied functions fcn and jacobian in parallel. This is done only if the function imsl_omp_options is called to flag user-defined functions as thread-safe. A function is thread-safe if there are no dependencies between calls. Such dependencies are usually the result of writing to global or static variables.
Examples
Example 1
In this example, the nonlinear least-squares problem
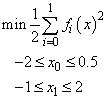
where
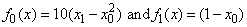
is solved with an initial guess (−1.2, 1.0).
#include <imsl.h>
#include <math.h>
#define M 2
#define N 2
#define LDFJAC 2
int main()
{
void rosbck(int, int, float *, float *);
int ibtype = 0;
float xlb[N] = {-2.0, -1.0};
float xub[N] = {0.5, 2.0};
float *x;
x =
imsl_f_bounded_least_squares (rosbck, M, N, ibtype,
xlb,
xub, 0);
printf("x[0] = %f\n", x[0]);
printf("x[1] = %f\n", x[1]);
}
void rosbck (int m, int n, float *x, float *f)
{
f[0] = 10.0*(x[1] - x[0]*x[0]);
f[1] = 1.0 - x[0];
}
Output
x[0] = 0.500000
x[1] = 0.250000
Example 2
This example solves the nonlinear least-squares problem
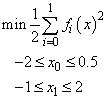
where
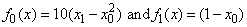
This time, an initial guess (−1.2, 1.0) is supplied, as well as the analytic Jacobian. The residual at the approximate solution is returned.
#include <imsl.h>
#include <math.h>
#define M 2
#define N 2
#define LDFJAC 2
int main()
{
void rosbck(int, int, float *, float *);
void jacobian(int, int, float *, float *, int);
int ibtype = 0;
float xlb[N] = {-2.0, -1.0};
float xub[N] = {0.5, 2.0};
float xguess[N] = {-1.2, 1.0};
float *fvec;
float *x;
x = imsl_f_bounded_least_squares (rosbck, M, N, ibtype, xlb, xub,
IMSL_JACOBIAN, jacobian,
IMSL_XGUESS, xguess,
IMSL_FVEC, &fvec,
0);
printf("x[0] = %f\n", x[0]);
printf("x[1] = %f\n\n", x[1]);
printf("fvec[0] = %f\n", fvec[0]);
printf("fvec[1] = %f\n\n", fvec[1]);
}
void rosbck (int m, int n, float *x, float *f)
{
f[0] = 10.0*(x[1] - x[0]*x[0]);
f[1] = 1.0 - x[0];
}
void jacobian (int m, int n, float *x, float *fjac, int fjac_col_dim)
{
fjac[0] = -20.0*x[0];
fjac[1] = 10.0;
fjac[2] = -1.0;
fjac[3] = 0.0;
}
Output
x[0] = 0.500000
x[1] = 0.250000
fvec[0] = 0.000000
fvec[1] = 0.500000
