Computes the value of a Hermite quintic spline or the value of one of its derivatives. In particular, computes solutions to the Feynman-Kac PDE handled by function imsl_f_feynman_kac.
Synopsis
#include <imsl.h>
float *imsl_f_feynman_kac_evaluate (int nw, int m, float breakpoints[], float w[], float coef[],…, 0)
The type double function is imsl_d_feynman_kac_evaluate.
Required Arguments
int nw
(Input)
Length of the array containing the evaluation points of the
spline.
int m
(Input)
Number of breakpoints for the Hermite quintic spline interpolation.
It is required that m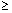
2. When applied to imsl_f_feynman_kac,
m is identical
to argument nxgrid.
float breakpoints[]
(Input)
Array of length m containing the
breakpoints for the Hermite quintic spline interpolation. The breakpoints must
be in strictly increasing order. When applied to imsl_f_feynman_kac,
breakpoints[] is
identical to array xgrid[].
float w[]
(Input)
Vector of length nw containing the
evaluation points for the spline. It is required that breakpoints[0]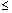 
w[i] 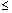breakpoints[m-1]
for
i=0,…,nw-1.
float coef[]
(Input)
Vector of length 3*m containing the
coefficients of the Hermite quintic spline.
When applied to imsl_f_feynman_kac,
this vector is one of the rows of output arrays y or y_prime related to the
spline coefficients at time points t=tgrid[j], j=1,…, ntgrid.
Return Value
A pointer to an array of length nw containing the values of the Hermite quintic spline or one of its derivatives at the evaluation points in array w[]. If no values can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_feynman_kac_evaluate(int nw, int m, float breakpoints[], float w[], float coef[],
IMSL_DERIV, int deriv,
IMSL_RETURN_USER, float value[],
0)
Optional Arguments
IMSL_DERIV, int deriv
(Input)
Let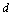 
= deriv and let 
be the given Hermite quintic spline.
Then, this option produces the d-th derivative of at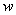 
, 
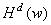. It is required that deriv = 0,1,2
or 3.
Default: deriv = 0.
IMSL_RETURN_USER,
float value[]
(Output)
A user defined array of length nw to receive the
d-th derivative of 
at the evaluation points in
w[]. When using
this option, the return value of the function is NULL.
Description
The Hermite quintic spline interpolation is done over the
composite interval 
, where breakpoints[i-1]
=
are given by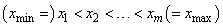 
.
The Hermite quintic spline function is constructed using three primary functions, defined by
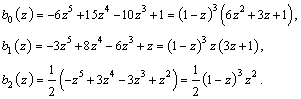
For each
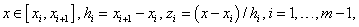
the spline is locally defined by
where
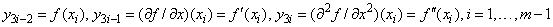
are the values of a given twice continuously differentiable
function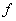 
and its first two derivatives at
the breakpoints.
The approximating function is twice continuously
differentiable on , whereas the third derivative is in
general only continuous within the interior of the intervals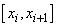 
. From the local representation of
it follows that
.
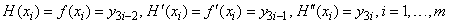The spline coefficients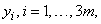 
are stored as successive
triplets in array coef[].
For a given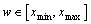 
, function imsl_f_feynman_kac_evaluate
uses the information in coef[]
together with the values of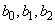 
and its derivatives at
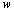to compute 
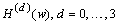using the local representation
on the particular subinterval containing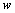 
.
Example
Consider function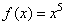 
, a polynomial of degree 5, on the
interval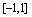 
with breakpoints 
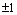. Then, the end derivative values are
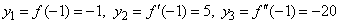
and
.
Since the Hermite quintic interpolates all polynomials up
to degree 5 exactly, the spline interpolation on 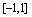must agree with the exact
function value up to rounding errors.
#include <imsl.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
/* Define function */
#define F(x) pow(x,5.0)
int main()
{
int i;
int nw = 7;
int m = 2;
float breakpoints[] = { -1.0, 1.0 };
float w[] = { -0.75, -0.5, -0.25, 0.0,
0.25, 0.5, 0.75 };
float coef[] = { -1.0, 5.0, -20.0,
1.0, 5.0, 20.0 };
float *result = NULL;
result = imsl_f_feynman_kac_evaluate(nw, m, breakpoints, w, coef, 0);
/* Print results */
printf(" x F(x) Interpolant Error\n\n");
for (i=0; i<=6; i++)
printf(" %6.3f %10.3f %10.3f %10.7f\n", w[i], F(w[i]),
result[i], fabs(F(w[i])-result[i]));
}
Output
x F(x) Interpolant Error
-0.750 -0.237 -0.237 0.0000000
-0.500 -0.031 -0.031 0.0000000
-0.250 -0.001 -0.001 0.0000000
0.000 0.000 0.000 0.0000000
0.250 0.001 0.001 0.0000000
0.500 0.031 0.031 0.0000000
0.750 0.237 0.237 0.0000000
