Computes the discrete Fourier cosine transformation of an even sequence.
Synopsis
#include <imsl.h>
float *imsl_f_fft_cosine (int n, float p[], …, 0)
The type double procedure is imsl_d_fft_cosine.
Required Arguments
int n
(Input)
Length of the sequence to be transformed. It must be greater than
1.
float p[]
(Input)
Array of size n containing the
sequence to be transformed.
Return Value
A pointer to the transformed sequence. To release this space, use imsl_free. If no solution was computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_fft_cosine (int n, float p[],
IMSL_RETURN_USER, float q[],
IMSL_PARAMS, float params[],
0)
Optional Arguments
IMSL_RETURN_USER, float q[]
(Output)
Store the result in the user-provided space pointed to by q. Therefore, no
storage is allocated for the solution, and imsl_f_fft_cosine
returns q. The
length of array must be at least n.
IMSL_PARAMS, float params[]
(Input)
Pointer returned by a previous call to imsl_f_fft_cosine_init. If imsl_f_fft_cosine is
used repeatedly with the same value of n, then it is more
efficient to compute these parameters only once.
Default: Initializing
parameters computed each time imsl_f_fft_cosine is
entered
Description
The function imsl_f_fft_cosine computes the discrete Fourier cosine transform of a real vector of size N. It uses the system’s high performance library for the computation, if available. Otherwise, the method used is a variant of the Cooley-Tukey algorithm, which is most efficient when N − 1 is a product of small prime factors. If N satisfies this condition, then the computational effort is proportional to N logN. Specifically, given an N-vector p, imsl_f_fft_cosine returns in q
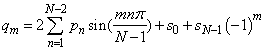
Finally, note that the Fourier cosine transform is its own (unnormalized) inverse. The Cooley-Tukey algorithm is based on the cosine FFT in FFTPACK, which was developed by Paul Swarztrauber at the National Center for Atmospheric Research.
Example
This example inputs a pure cosine wave as a data vector and recovers its Fourier cosine series, which is a vector with all components zero, except n − 1 at the appropriate frequency.
#include <imsl.h>
#include <math.h>
#include <stdio.h>
int main()
{
int n = 7;
int i;
float p[7];
float *q;
float pi;
pi = imsl_f_constant("pi", 0);
/* Fill p with a pure cosine wave */
for (i=0; i<n; i++)
p[i] = cos((float)(i)*pi/(float)(n-1));
q = imsl_f_fft_cosine (n, p, 0);
printf (" index\t p\t q\n");
for (i=0; i<n; i++)
printf("\t%1d\t%5.2f\t%5.2f\n", i, p[i], q[i]);
}
Output
index p q
0 1.00 -0.00
1 0.87 6.00
2 0.50 0.00
3 -0.00 0.00
4 -0.50 -0.00
5 -0.87 -0.00
6 -1.00 -0.00

