Computes the real discrete Fourier transform of a real sequence.
Synopsis
#include <imsl.h>
float *imsl_f_fft_real (int n, float p[], …, 0)
The type double function is imsl_d_fft_real.
Required Arguments
int n
(Input)
Length of the sequence to be transformed.
float p[]
(Input)
Array with n components
containing the periodic sequence.
Return Value
A pointer to the transformed sequence. To release this space, use imsl_free. If no value can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_fft_real (int n, float p[],
IMSL_BACKWARD,
IMSL_PARAMS, float params[],
IMSL_RETURN_USER, float q[],
0)
Optional Arguments
IMSL_BACKWARD
Compute the
backward transform. If IMSL_BACKWARD is used,
the return value of the function is the backward transformed sequence.
IMSL_PARAMS, float params[]
(Input)
Pointer returned by a previous call to imsl_f_fft_real_init.
If imsl_f_fft_real is
used repeatedly with the same value of n, then it is more
efficient to compute these parameters only once.
IMSL_RETURN_USER, float q[]
(Output)
Store the result in the user-provided space pointed to by q. Therefore, no
storage is allocated for the solution, and imsl_f_fft_real
returns q. The
array q must be
at least n
long.
Description
The function imsl_f_fft_real computes the discrete Fourier transform of a real vector of size n. It uses the system’s high performance library for the computation, if available. Otherwise, the method used is a variant of the Cooley-Tukey algorithm, which is most efficient when n is a product of small prime factors. If n satisfies this condition, then the computational effort is proportional to n log n. The Cooley-Tukey algorithm is based on the real FFT in FFTPACK, which was developed by Paul Swarztrauber at the National Center for Atmospheric Research.
By default, imsl_f_fft_real computes the forward transform. If n is even, then the forward transform is
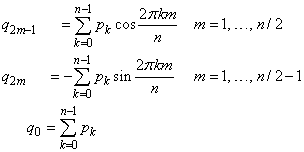
If n is odd, qm is defined as above for m from 1 to (n − 1)/2.
Let f be a real valued function of time. Suppose we sample f at n equally spaced time intervals of length Δ seconds starting at time t0. That is, we have
pi:= f(t0 + iΔ) i = 0, 1, …, n − 1
We will assume that n is odd for the remainder of this discussion. The function imsl_f_fft_real treats this sequence as if it were periodic of period n. In particular, it assumes that f(t0) = f(t0 + nΔ). Hence, the period of the function is assumed to be T = nΔ. We can invert the above transform for p as follows:
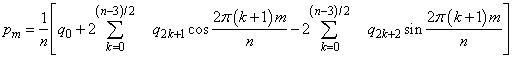
This formula is very revealing. It can be interpreted in the following manner. The coefficients q produced by imsl_f_fft_real determine an interpolating trigonometric polynomial to the data. That is, if we define
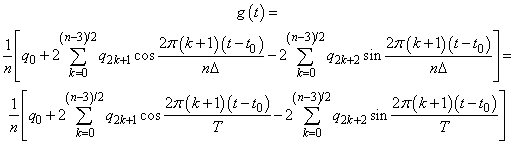
then we have
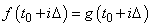
Now suppose we want to discover the dominant frequencies, forming the vector P of length (n + 1)/2 as follows:
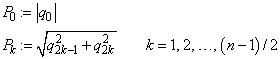
These numbers correspond to the energy in the spectrum of the signal. In particular, Pk corresponds to the energy level at frequency
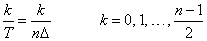
Furthermore, note that there are only (n + 1)/2 ≈ T/(2Δ) resolvable frequencies when n observations are taken. This is related to the Nyquist phenomenon, which is induced by discrete sampling of a continuous signal. Similar relations hold for the case when n is even.
If the optional argument IMSL_BACKWARD is specified, then the backward transform is computed. If n is even, then the backward transform is
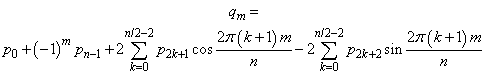
If n is odd,
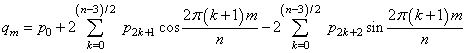
The backward Fourier transform is the unnormalized inverse of the forward Fourier transform.
Examples
Example 1
In this example, a pure cosine wave is used as a data vector, and its Fourier series is recovered. The Fourier series is a vector with all components zero except at the appropriate frequency where it has an n.
#include <imsl.h>
#include <math.h>
#include <stdio.h>
int main()
{
int k, n = 7;
float two_pi = 2*imsl_f_constant("pi", 0);
float p[7], *q;
/* Fill q with a pure exponential signal */
for (k = 0; k < n; k++)
p[k] = cos(k*two_pi/n);
q = imsl_f_fft_real (n, p, 0);
printf(" index p q\n");
for (k = 0; k < n; k++)
printf("%11d%10.2f%10.2f\n", k, p[k], q[k]);
}
Output
index p q
0 1.00 0.00
1 0.62 3.50
2 -0.22 0.00
3 -0.90 -0.00
4 -0.90 -0.00
5 -0.22 0.00
6 0.62 -0.00
Example 2
This example computes the Fourier transform of the vector x, where xj = (−1)j for j = 0 to n − 1. The backward transform of this vector is now computed by using the optional argument IMSL_BACKWARD. Note that s = nx, that is, sj = (−1)jn, for j = 0 to n − 1.
#include <imsl.h>
#include <stdio.h>
int main()
{
int k, n = 7;
float *q, *s, x[7];
/* Fill data vector */
x[0] = 1.0;
for (k = 1; k<n; k++)
x[k] = -x[k-1];
/* Compute the forward transform of x */
q = imsl_f_fft_real (n, x, 0);
/* Compute the backward transform of x */
s = imsl_f_fft_real (n, q,
IMSL_BACKWARD,
0);
printf(" index x q s\n");
for (k = 0; k < n; k++)
printf("%11d%10.2f%10.2f%10.2f\n", k, x[k], q[k], s[k]);
}
Output
index x q s
0 1.00 1.00 7.00
1 -1.00 1.00 -7.00
2 1.00 0.48 7.00
3 -1.00 1.00 -7.00
4 1.00 1.25 7.00
5 -1.00 1.00 -7.00
6 1.00 4.38 7.00

