Integrates a function with singularity points given.
Synopsis
#include <imsl.h>
float imsl_f_int_fcn_sing_pts (float fcn(), float a, float b, int npoints, float points[], …, 0)
The type double function is imsl_d_int_fcn_sing_pts.
Required Arguments
float fcn (float x)
(Input)
User-supplied function to be integrated.
float a
(Input)
Lower limit of integration.
float b
(Input)
Upper limit of integration.
int npoints
(Input)
The number of singularities of the integrand.
float points[]
(Input)
The abscissas of the singularities. These values should be interior
to the interval [a, b].
Return Value
The value of
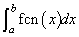
is returned. If no value can be computed, NaN is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float imsl_f_int_fcn_sing_pts (float fcn(), float a, float b, int npoints, float points[],
IMSL_ERR_ABS, float err_abs,
IMSL_ERR_REL, float err_rel,
IMSL_ERR_EST, float *err_est,
IMSL_MAX_SUBINTER, int max_subinter,
IMSL_N_SUBINTER, int *n_subinter,
IMSL_N_EVALS, int *n_evals,
IMSL_FCN_W_DATA, float fcn(), void *data,
0)
Optional Arguments
IMSL_ERR_ABS, float err_abs
(Input)
Absolute accuracy desired.
Default: 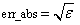 where ɛ is the machine
precision
where ɛ is the machine
precision
IMSL_ERR_REL, float err_rel
(Input)
Relative accuracy desired.
Default: 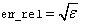 where ɛ is the machine
precision
where ɛ is the machine
precision
IMSL_ERR_EST, float *err_est
(Output)
Address to store an estimate of the absolute value of the error.
IMSL_MAX_SUBINTER, int max_subinter
(Input)
Number of subintervals allowed.
Default: max_subinter = 500
IMSL_N_SUBINTER, int *n_subinter
(Output)
Address to store the number of subintervals generated.
IMSL_N_EVALS, int *n_evals
(Output)
Address to store the number of evaluations of fcn.
IMSL_FCN_W_DATA, float fcn (float x, void *data), void *data
(Input)
User supplied function to be integrated, which also accepts a pointer
to data that is supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
Description
The function imsl_f_int_fcn_sing_pts is a special-purpose integrator that uses a globally adaptive scheme in order to reduce the absolute error. It subdivides the interval [a, b] into npoints + 1 user-supplied subintervals and uses a 21-point Gauss-Kronrod rule to estimate the integral over each subinterval. The error for each subinterval is estimated by comparison with the 10-point Gauss quadrature rule. The subinterval with the largest estimated error is then bisected, and the same procedure is applied to both halves. The bisection process is continued until either the error criterion is satisfied, roundoff error is detected, the subintervals become too small, or the maximum number of subintervals allowed is reached. This function uses an extrapolation procedure known as the ɛ-algorithm.
On some platforms,imsl_f_int_fcn_sing_pts can evaluate the user-supplied function fcn in parallel. This is done only if the function imsl_omp_options is called to flag user-defined functions as thread-safe. A function is thread-safe if there are no dependencies between calls. Such dependencies are usually the result of writing to global or static variables.
The function imsl_f_int_fcn_sing_pts is based on the subroutine QAGP by Piessens et al. (1983).
Examples
Example 1
The value of
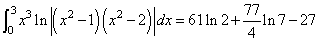
is computed. The values of the actual and estimated error are machine dependent. Note that this function never evaluates the user-supplied function at the user-supplied breakpoints.
#include <math.h>
#include <imsl.h>
float fcn(float x);
int main()
{
int npoints = 2;
float q, exact, points[2];
/* Set singular points */
points[0] = 1.0;
points[1] = sqrt(2.);
imsl_omp_options(IMSL_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
/* Evaluate the integral */
q = imsl_f_int_fcn_sing_pts (fcn, 0.0, 3.0, npoints, points, 0);
/* print the result and */
/* the exact answer */
exact = 61.*log(2.) + (77./4)*log(7.) - 27.;
printf("integral = %10.3f\nexact = %10.3f\n", q, exact);
}
float fcn(float x)
{
return x*x*x*(log(fabs((x*x-1.)*(x*x-2.))));
}
Output
integral = 52.741
exact = 52.741
Example 2
The value of

is again computed. The values of the actual and estimated error are printed as well. Note that these numbers are machine dependent. Furthermore, the error estimate is usually pessimistic. That is, the actual error is usually smaller than the error estimate, as in this example. The number of function evaluations also are printed.
#include <math.h>
#include <imsl.h>
float fcn(float x);
int main()
{
int n_evals, npoints = 2;
float q, exact, err_est, exact_err, points[2];
/* Set singular points */
points[0] = 1.0;
points[1] = sqrt(2.);
imsl_omp_options(IMSL_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
/* Evaluate the integral and get the */
/* error estimate and the number of */
/* evaluations */
q = imsl_f_int_fcn_sing_pts (fcn, 0.0, 3.0, npoints, points,
IMSL_ERR_EST, &err_est,
IMSL_N_EVALS, &n_evals,
0);
/* Print the result and the */
/* exact answer */
exact = 61.*log(2.) + (77./4)*log(7.) - 27.;
exact_err = fabs(exact - q);
printf("integral = %10.3f\nexact = %10.3f\n", q, exact);
printf("error estimate = %e\nexact error = %e\n", err_est,
exact_err);
printf("The number of function evaluations = %d\n", n_evals);
}
float fcn(float x)
{
return x*x*x*(log(fabs((x*x-1.)*(x*x-2.))));
}
Output
integral = 52.741
exact = 52.741
error estimate = 1.258850e-04
exact error = 3.051758e-05
The number of function evaluations = 819
Warning Errors
|
IMSL_ROUNDOFF_CONTAMINATION
|
Roundoff error, preventing the requested tolerance from being achieved, has been detected. |
|
IMSL_PRECISION_DEGRADATION |
A degradation in precision has been detected. |
|
IMSL_EXTRAPOLATION_ROUNDOFF |
Roundoff error has been detected in the extrapolation table. The tolerances, “err_abs” = # and “err_rel” = # cannot be reached. |
Fatal Errors
|
IMSL_DIVERGENT |
Integral is probably divergent or slowly convergent. |

