Chapter 1: Linear Systems > lin_sol_gen_band (complex)

lin_sol_gen_band (complex)

TextonSpedometerHPClogo.gif

Solves a complex general band system of linear equations Ax = b. Using optional arguments, any of several related computations can be performed. These extra tasks include computing the LU factorization of A using partial pivoting, solving AHx = b, or computing the solution of Ax = b given the LU factorization of A.

Synopsis

#include <imsl.h>

f_complex *imsl_c_lin_sol_gen_band (int n, f_complex a[], int nlca, int nuca, f_complex b[], …, 0)

The type double procedure is imsl_z_lin_sol_gen_band.

Required Arguments

int n   (Input)
Number of rows and columns in the matrix.

f_complex a[]   (Input)
Array of size (nlca + nuca + 1) × n containing the n × n banded coefficient matrix in band storage mode.

int nlca   (Input)
Number of lower codiagonals in a.

int nuca   (Input)
Number of upper codiagonals in a.

f_complex b[] (Input)
Array of size n containing the right-hand side.

Return Value

A pointer to the solution x of the linear system Ax = b. To release this space use imsl_free. If no solution was computed, NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

f_complex *imsl_c_lin_sol_gen_band (int n, f_complex a[],int nlca, int nuca, f_complex b[],

IMSL_TRANSPOSE,

IMSL_RETURN_USER, f_complex x[],

IMSL_FACTOR, int **p_pvt, f_complex **p_factor,

IMSL_FACTOR_USER, int pvt[], f_complex factor[],

IMSL_CONDITION, float *condition,

IMSL_FACTOR_ONLY,

IMSL_SOLVE_ONLY,

0)

Optional Arguments

IMSL_TRANSPOSE
Solve AHx = b
Default: Solve Ax = b.

IMSL_RETURN_USER, f_complex x[]  (Output)
A user-allocated array of length n containing the solution x.

IMSL_FACTOR, int **p_pvt, f_complex **p_factor   (Output)

int **p_pvt   (Input/Output)
The address of a pointer to an array of length n containing the pivot sequence for the factorization. On return, the necessary space is allocated by imsl_c_lin_sol_gen_band. Typically, int *p_pvt is declared and &p_pvt is used as an argument.

f_complex **p_factor   (Input/Output)
The address of a pointer to an array of size (2nlca + nuca + 1) × n containing the LU factorization of A with column pivoting. On return, the necessary space is allocated by imsl_c_lin_sol_gen_band. Typically, f_complex *p_factor is declared and &p_factor is used as an argument.

IMSL_FACTOR_USER, int pvt[], f_complex factor[]   (Input/Output)

int pvt[]   (Input/Output)
A user-allocated array of size n containing the pivot sequence for the factorization.

f_complex factor[]   (Input/Output)
A user-allocated array of size (2nlca + nuca + 1) × n containing the LU factorization of A. If A is not needed, factor and a can share the first (nlca + nuca + 1) × n locations.

            These parameters are “Input” if IMSL_SOLVE_ONLY is specified. They are “Output” otherwise.

IMSL_CONDITION, float *condition   (Output)
A pointer to a scalar containing an estimate of the L1 norm condition number of the matrix A. This option cannot be used with the option IMSL_SOLVE_ONLY.

IMSL_FACTOR_ONLY
Compute the LU factorization of A with partial pivoting. If IMSL_FACTOR_ONLY is used, either IMSL_FACTOR or IMSL_FACTOR_USER is required. The argument b is then ignored, and the returned value of imsl_c_lin_sol_gen_band is NULL.

IMSL_SOLVE_ONLY
Solve Ax = b given the LU factorization previously computed by imsl_c_lin_sol_gen_band. By default, the solution to Ax = b is pointed to by imsl_c_lin_sol_gen_band. If IMSL_SOLVE_ONLY is used, argument IMSL_FACTOR_USER is required and argument a is ignored.

Description

The function imsl_c_lin_sol_gen_band solves a system of linear algebraic equations with a complex band matrix A. It first computes the LU factorization of A using scaled partial pivoting. Scaled partial pivoting differs from partial pivoting in that the pivoting strategy is the same as if each row were scaled to have the same L∝ norm. The factorization fails if U has a zero diagonal element. This can occur only if A is singular or very close to a singular matrix.

The solution of the linear system is then found by solving two simpler systems, y = L-1b and x = U -1y. When the solution to the linear system or the inverse of the matrix is sought, an estimate of the L1 condition number of A is computed using Higham’s modifications to Hager’s method, as given in Higham (1988). If the estimated condition number is greater than 1/ɛ (where ɛ is the machine precision), a warning message is issued. This indicates that very small changes in A may pro­duce large changes in the solution x. The function imsl_c_lin_sol_gen_band fails if U, the upper triangular part of the factorization, has a zero diagonal element. The function imsl_c_lin_sol_gen_band is based on the LINPACK subroutine CGBFA; see Dongarra et al. (1979). CGBFA uses unscaled partial pivoting.

Examples

Example 1

The following linear system is solved:

 

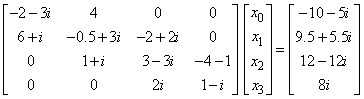
#include <imsl.h>

 

int main()

{

        int          n = 4;

        int          nlca = 1;

        int          nuca = 1;

        f_complex    *x;

 

                     /* Note that a is in band storage mode */

 

        f_complex    a[] =

                {{0.0, 0.0}, {4.0, 0.0}, {-2.0, 2.0}, {-4.0, -1.0},

                {-2.0, -3.0}, {-0.5, 3.0}, {3.0, -3.0}, {1.0, -1.0},

                {6.0, 1.0}, {1.0, 1.0}, {0.0, 2.0}, {0.0, 0.0}};

 

        f_complex    b[] =

                {{-10.0, -5.0}, {9.5, 5.5}, {12.0, -12.0}, {0.0, 8.0}};

 

        x = imsl_c_lin_sol_gen_band (n, a, nlca, nuca, b, 0);

 

        imsl_c_write_matrix ("Solution, x, of Ax = b", n, 1, x, 0);

}

Output

  Solution, x, of Ax = b

1  (         3,        -0)

2  (        -1,         1)

3  (         3,         0)

4  (        -1,         1)

Example 2

This example solves the problem Ax = b using the data from the first example. This time, the factorizations are returned and then the problem AHx = b is solved without recomputing LU.

 

#include <imsl.h>

 

#include <stdlib.h>

int main()

{

        int            n = 4;

        int            nlca = 1;

        int            nuca = 1;

        int           *pivot;

        f_complex     *x;

        f_complex     *factor;

 

                        /* Note that a is in band storage mode */

 

        f_complex      a[] =

                {{0.0, 0.0}, {4.0, 0.0}, {-2.0, 2.0}, {-4.0, -1.0},

                {-2.0, -3.0}, {-0.5, 3.0}, {3.0, -3.0}, {1.0, -1.0},

                {6.0, 1.0}, {1.0, 1.0}, {0.0, 2.0}, {0.0, 0.0}};

        f_complex      b[] =

                {{-10.0, -5.0}, {9.5, 5.5}, {12.0, -12.0}, {0.0, 8.0}};

 

                        /* Solve Ax = b and return LU */

 

        x = imsl_c_lin_sol_gen_band (n, a, nlca, nuca, b,

                IMSL_FACTOR, &pivot, &factor,

                0);

 

        imsl_c_write_matrix ("solution of Ax = b", n, 1, x, 0);

        imsl_free (x);

 

                        /* Use precomputed LU to solve ctrans(A)x = b */

 

        x = imsl_c_lin_sol_gen_band (n, a, nlca, nuca, b,

                IMSL_FACTOR_USER, pivot, factor,

                IMSL_TRANSPOSE,

                0);

 

        imsl_c_write_matrix ("solution of ctrans(A)x = b", n, 1, x, 0);

}

 

 

Output

    solution of Ax = b

1  (         3,        -0)

2  (        -1,         1)

3  (         3,         0)

4  (        -1,         1)

 

solution of ctrans(A)x = b

1  (      5.58,     -2.91)

2  (     -0.48,     -4.67)

3  (     -6.19,      7.15)

4  (     12.60,     30.20)

Warning Errors

IMSL_ILL_CONDITIONED                         The input matrix is too ill-conditioned. An estimate of the reciprocal of its L1 condition number is “rcond” = #. The solution might not be accurate.

Fatal Errors

IMSL_SINGULAR_MATRIX                         The input matrix is singular.

RW_logo.jpg
Contact Support