lin_sol_gen (complex)

Chapter 1: Linear Systems > lin_sol_gen (complex)

lin_sol_gen (complex)

Solves a complex general system of linear equations Ax = b. Using optional arguments, any of several related computations can be performed. These extra tasks include computing the LU factorization of A using partial pivoting, computing the inverse matrix A^-1, solving AHx = b, or computing the solution of Ax = b given the LU factorization of A.

Synopsis

#include <imsl.h>

f_complex *imsl_c_lin_sol_gen (int n, f_complex a[], f_complex b[], …, 0)

The type d_complex procedure is imsl_z_lin_sol_gen.

Required Arguments

int n (Input)
Number of rows and columns in the matrix.

f_complex a[] (Input)
Array of size n × n containing the matrix.

f_complex b[] (Input)
Array of length n containing the right-hand side.

Return Value

A pointer to the solution x of the linear system Ax = b. To release this space, use imsl_free. If no solution was computed, then NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

f_complex *imsl_c_lin_sol_gen (int n, f_complex a[], f_complex b[],

IMSL_A_COL_DIM, int a_col_dim,

IMSL_TRANSPOSE,

IMSL_RETURN_USER, f_complex x[],

IMSL_FACTOR, int **p_pvt, f_complex **p_factor,

IMSL_FACTOR_USER, int pvt[], f_complex factor[],

IMSL_FAC_COL_DIM, int fac_col_dim,

IMSL_INVERSE, f_complex **p_inva,

IMSL_INVERSE_USER, f_complex inva[],

IMSL_INV_COL_DIM, int inva_col_dim,

IMSL_CONDITION, float *cond,

IMSL_FACTOR_ONLY,

IMSL_SOLVE_ONLY,

IMSL_INVERSE_ONLY,

Optional Arguments

IMSL_A_COL_DIM, int a_col_dim (Input)
The column dimension of the array a.
Default: a_col_dim = n

IMSL_TRANSPOSE
Solve AHx = b
Default: Solve Ax = b

IMSL_RETURN_USER, f_complex x[] (Output)
A user-allocated array of length n containing the solution x.

IMSL_FACTOR, int **p_pvt, f_complex **p_factor (Output)

int **p_pvt (Output)
The address of a pointer to an array of length n containing the pivot sequence for the factorization. On return, the necessary space is allocated by imsl_c_lin_sol_gen. Typically, int *p_pvt is declared, and &p_pvt is used as an argument.

f_complex **p_factor (Output)
The address of a pointer to an array of size n × n containing the LU factorization of A with column pivoting. On return, the necessary space is allocated by imsl_c_lin_sol_gen. The lower-triangular part of this array contains information necessary to construct L, and the upper-triangular part contains U. Typically, f_complex *p_factor is declared, and &p_factor is used as an argument.

IMSL_FACTOR_USER, int pvt[], f_complex factor[] (Input/Output)

int pvt[] (Input/Output)
A user-allocated array of size n containing the pivot sequence for the factorization.

f_complex factor[] (Input/Output)
A user-allocated array of size n × n containing the LU factorization of A. The lower-triangular part of this array contains information necessary to construct L, and the upper-triangular part contains U.

These parameters are input if IMSL_SOLVE is specified. They are output otherwise. If A is not needed, factor and a can share the same storage.

IMSL_FAC_COL_DIM, int fac_col_dim (Input)
The column dimension of the array containing the LU factorization of A.
Default: fac_col_dim = n

IMSL_INVERSE, f_complex **p_inva (Output)
The address of a pointer to an array of size n × n containing the inverse of the matrix A. On return, the necessary space is allocated by imsl_c_lin_sol_gen. Typically, f_complex *p_inva is declared, and &p_inva is used as an argument.

IMSL_INVERSE_USER, f_complex inva[] (Output)
A user-allocated array of size n × n containing the inverse of A.

IMSL_INV_COL_DIM, int inva_col_dim (Input)
The column dimension of the array containing the inverse of A.
Default: inva_col_dim = n

IMSL_CONDITION, float *cond (Output)
A pointer to a scalar containing an estimate of the L1 norm condition number of the matrix A. Do not use this option with IMSL_SOLVE_ONLY.

IMSL_FACTOR_ONLY
Compute the LU factorization of A with partial pivoting. If IMSL_FACTOR_ONLY is used, either IMSL_FACTOR or IMSL_FACTOR_USER is required. The argument b is then ignored, and the returned value of imsl_c_lin_sol_gen is NULL.

IMSL_SOLVE_ONLY
Solve Ax = b given the LU factorization previously computed by imsl_c_lin_sol_gen. By default, the solution to Ax = b is pointed to by imsl_c_lin_sol_gen. If IMSL_SOLVE_ONLY is used, argument IMSL_FACTOR_USER is required and argument a is ignored.

IMSL_INVERSE_ONLY
Compute the inverse of the matrix A. If IMSL_INVERSE_ONLY is used, either IMSL_INVERSE or IMSL_INVERSE_USER is required. Argument b is then ignored, and the returned value of imsl_c_lin_sol_gen is NULL.

Description

The function imsl_c_lin_sol_gen solves a system of linear algebraic equations with a complex coefficient matrix A. It first computes the LU factorization of A with partial pivoting such that L^-1A = U. Let F be the matrix p_factor returned by optional argument IMSL_FACTOR. The triangular matrix U is stored in the upper triangle of F. The strict lower triangle of F contains the information needed to reconstruct L^-¹ using

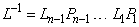
The factors Pi and Li are defined by partial pivoting. Piis the identity matrix with rows i and p_pvt[i-1] interchanged. L_i is the identity matrix with Fji, for j = i + 1,…, n, inserted below the diagonal in column i.

The solution of the linear system is then found by solving two simpler systems, y = L^-1b and x = U ^-1y. When the solution to the linear system or the inverse of the matrix is computed, an estimate of the L1 condition number of A is computed using the same algorithm as in Dongarra et al. (1979). If the estimated condition number is greater thasn 1∕ɛ (where ɛ is the machine precision), a warning message is issued. This indicates that very small changes in A may produce large changes in the solution x. The function imsl_c_lin_sol_gen fails if U, the upper-triangular part of the factorization, has a zero diagonal element.

Examples

Example 1

This example solves a system of three linear equations. The equations are:

(1 + i) x1 + (2 + 3i) x2 + (3 − 3i) x3 = 3 + 5i

(2 + i) x1 + (5 + 3i) x2 + (7 − 5i) x3 = 22 + 10i

(−2 + i) x1 + (−4 + 4i) x2 + (5 + 3i) x3 = −10 + 4i

#include <imsl.h>

f_complex a[] = {{1.0, 1.0}, {2.0, 3.0}, {3.0, -3.0},

{2.0, 1.0}, {5.0, 3.0}, {7.0, -5.0},

{-2.0, 1.0}, {-4.0, 4.0}, {5.0, 3.0}};

f_complex b[] = {{3.0, 5.0}, {22.0, 10.0}, {-10.0, 4.0}};

int main()

{

int n = 3;

f_complex *x;

/* Solve Ax = b for x */

x = imsl_c_lin_sol_gen (n, a, b, 0);

/* Print x */

imsl_c_write_matrix ("Solution, x, of Ax = b", 1, n, x, 0);

}

Output

Solution, x, of Ax = b

1 2 3

( 1, -1) ( 2, 4) ( 3, -0)

Example 2

This example solves the conjugate transpose problem AHx = b and returns the LU factorization of A using partial pivoting. This example differs from the first example in that the solution array is allocated in the main program.

#include <imsl.h>

f_complex a[] = {{1.0, 1.0}, {2.0, 3.0}, {3.0, -3.0},

{2.0, 1.0}, {5.0, 3.0}, {7.0, -5.0},

{-2.0, 1.0}, {-4.0, 4.0}, {5.0, 3.0}};

f_complex b[] = {{3.0, 5.0}, {22.0, 10.0}, {-10.0, 4.0}};

int main()

{

int n = 3, pvt[3];

f_complex factor[9];

f_complex x[3];

/* Solve ctrans(A)*x = b for x */

imsl_c_lin_sol_gen (n, a, b,

IMSL_TRANSPOSE,

IMSL_RETURN_USER, x,

IMSL_FACTOR_USER, pvt, factor,

0);

/* Print x */

imsl_c_write_matrix ("Solution, x, of ctrans(A)x = b", 1, n, x, 0);

/* Print factors and pivot sequence */

imsl_c_write_matrix ("LU factors of A", n, n, factor, 0);

imsl_i_write_matrix ("Pivot sequence", 1, n, pvt, 0);

}

Output

Solution, x, of ctrans(A)x = b

1 2 3

( -9.79, 11.23) ( 2.96, -3.13) ( 1.85, 2.47)

LU factors of A

1 2 3

1 ( -2.000, 1.000) ( -4.000, 4.000) ( 5.000, 3.000)

2 ( 0.600, 0.800) ( -1.200, 1.400) ( 2.200, 0.600)

3 ( 0.200, 0.600) ( -1.118, 0.529) ( 4.824, 1.294)

Pivot sequence

1 2 3

3 3 3

Example 3

This example computes the inverse of the 3 × 3 matrix A in the first example and also solves the linear system. The product matrix C = A^-1A is computed as a check. The approximate result is C = I.

#include <imsl.h>

f_complex a[] = {{1.0, 1.0}, {2.0, 3.0}, {3.0, -3.0},

{2.0, 1.0}, {5.0, 3.0}, {7.0, -5.0},

{-2.0, 1.0}, {-4.0, 4.0}, {5.0, 3.0}};

f_complex b[] = {{3.0, 5.0}, {22.0, 10.0}, {-10.0, 4.0}};

int main()

{

int n = 3;

f_complex *x;

f_complex *p_inva;

f_complex *C;

/* Solve Ax = b for x */

x = imsl_c_lin_sol_gen (n, a, b,

IMSL_INVERSE, &p_inva,

0);

/* Print solution */

imsl_c_write_matrix ("Solution, x, of Ax = b", 1, n, x, 0);

/* Print input and inverse matrices */

imsl_c_write_matrix ("Input A", n, n, a, 0);

imsl_c_write_matrix ("Inverse of A", n, n, p_inva, 0);

/* Check and print result */

C = imsl_c_mat_mul_rect ("A*B",

IMSL_A_MATRIX, n,n, p_inva,

IMSL_B_MATRIX, n,n, a,

0);

imsl_c_write_matrix ("Product, inv(A)*A", n, n, C, 0);

}

Output

Solution, x, of Ax = b

1 2 3

( 1, -1) ( 2, 4) ( 3, -0)

Input A

1 2 3

1 ( 1, 1) ( 2, 3) ( 3, -3)

2 ( 2, 1) ( 5, 3) ( 7, -5)

3 ( -2, 1) ( -4, 4) ( 5, 3)

Inverse of A

1 2 3

1 ( 1.330, 0.594) ( -0.151, 0.028) ( -0.604, 0.613)

2 ( -0.632, -0.538) ( 0.160, 0.189) ( 0.142, -0.245)

3 ( -0.189, 0.160) ( 0.193, -0.052) ( 0.024, 0.042)

Product, inv(A)*A

1 2 3

1 ( 1, -0) ( -0, -0) ( -0, 0)

2 ( 0, 0) ( 1, 0) ( 0, -0)

3 ( -0, -0) ( -0, 0) ( 1, 0)

Warning Errors

IMSL_ILL_CONDITIONED The input matrix is too ill-conditioned. An estimate of the reciprocal of the L1 condition number is “rcond” = #. The solution might not be accurate.

Fatal Errors

IMSL_SINGULAR_MATRIX The input matrix is singular.

Contact Support