Minimizes a function f(x) of n variables using a quasi-Newton method.
Synopsis
#include <imsl.h>
float *imsl_f_min_uncon_multivar (float fcn(), int n, …, 0)
The type double function is imsl_d_min_uncon_multivar.
Required Arguments
float fcn (int n, float x[])
(Input/Output)
User-supplied function to evaluate the function to be
minimized where n is the size of x, x is the point at
which the function is evaluated, and fcn is the computed
function value at the point x.
int n
(Input)
Number of variables.
Return Value
A pointer to the minimum point x of the function. To release this space, use imsl_free. If no solution can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_min_uncon_multivar (float fcn(), int n,
IMSL_XGUESS, float xguess[],
IMSL_GRAD, void grad(),
IMSL_XSCALE, float xscale[],
IMSL_FSCALE, float fscale,
IMSL_GRAD_TOL, float grad_tol,
IMSL_STEP_TOL, float step_tol,
IMSL_MAX_STEP, float max_step,
IMSL_GOOD_DIGIT, int ndigit,
IMSL_MAX_ITN, int max_itn,
IMSL_MAX_FCN, int max_fcn,
IMSL_MAX_GRAD, int max_grad,
IMSL_INIT_HESSIAN, int ihess,
IMSL_RETURN_USER, float x[],
IMSL_FVALUE, float *fvalue,
IMSL_FCN_W_DATA, float fcn(), void *data,
IMSL_GRADIENT_W_DATA, void grad(), void *data,
0)
Optional Arguments
IMSL_XGUESS, float xguess[]
(Input)
Array with n components
containing an initial guess of the computed solution.
Default: xguess = 0
IMSL_GRAD, void grad (int n, float x[], float g[])
(Input/Output)
User-supplied function to compute the gradient at the point
x where n is the size of x, x is the point at
which the gradient is evaluated, and g is the computed
gradient at the point x.
IMSL_XSCALE, float xscale[]
(Input)
Array with n components
containing the scaling vector for the variables. xscale is used mainly
in scaling the gradient and the distance between two points. See keywords IMSL_GRAD_TOL and
IMSL_STEP_TOL
for more details.
Default: xscale[] = 1.0
IMSL_FSCALE, float fscale
(Input)
Scalar containing the function scaling. fscale is used mainly
in scaling the gradient. See keyword IMSL_GRAD_TOL for more
details.
Default: fscale = 1.0
IMSL_GRAD_TOL, float grad_tol
(Input)
Scaled gradient tolerance. The i-th component of the scaled
gradient at x is
calculated as
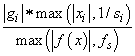
where g = ∇ f(x), s = xscale, and
fs = fscale.
Default:
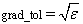 ,
, 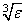 in double where ɛ is the machine
precision.
in double where ɛ is the machine
precision.
IMSL_STEP_TOL, float step_tol
(Input)
Scaled step tolerance. The i-th component of the scaled step
between two points x and y is computed as
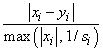
where s = xscale.
Default:
step_tol = ɛ2/3
IMSL_MAX_STEP, float max_step
(Input)
Maximum allowable step size.
Default: max_step = 1000
max (ɛ1, ɛ2) where,
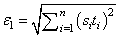
ɛ2 = ||s||2, s = xscale, and t = xguess.
IMSL_GOOD_DIGIT, int ndigit
(Input)
Number of good digits in the function. The default is machine
dependent.
IMSL_MAX_ITN, int max_itn
(Input)
Maximum number of iterations.
Default: max_itn = 100
IMSL_MAX_FCN, int max_fcn
(Input)
Maximum number of function evaluations.
Default: max_fcn = 400
IMSL_MAX_GRAD, int max_grad
(Input)
Maximum number of gradient evaluations.
Default: max_grad = 400
IMSL_INIT_HESSIAN, int ihess
(Input)
Hessian initialization parameter. If ihess is zero, the
Hessian is initialized to the identity matrix; otherwise, it is initialized to a
diagonal matrix containing
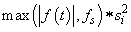
on the diagonal where t = xguess, fs = fscale, and
s = xscale.
Default:
ihess = 0
IMSL_RETURN_USER, float x[]
(Output)
User-supplied array with n components
containing the computed solution.
IMSL_FVALUE, float *fvalue
(Output)
Address to store the value of the function at the computed
solution.
IMSL_FCN_W_DATA, float fcn (int n, float x[], void *data),
void *data,
(Input)
User supplied function to compute the value of the function to be
minimized, which also accepts a pointer to data that is supplied by the user.
data is a
pointer to the data to be passed to the user-supplied function. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
IMSL_GRADIENT_W_DATA, void grad (int n, float x[], float g[], void *data),
void *data,
(Input)
User supplied function to compute the gradient at the point x, which also accepts
a pointer to data that is supplied by the user. data is a pointer to
the data to be passed to the user-supplied function. See the Introduction, Passing Data to
User-Supplied Functions at the beginning of this manual for more
details.
Description
The function f_min_uncon_multivar uses a quasi-Newton method to find the minimum of a function f(x) of n variables. The problem is stated as follows:

Given a starting point xc, the search direction is computed according to the formula
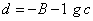
where B is a positive definite approximation of the Hessian, and gc is the gradient evaluated at xc. A line search is then used to find a new point
xn = xc + λd, λ > 0
such that
f(xn) ≤ f(xc) + αgTd, α ∈ (0, 0.5)
Finally, the optimality condition ||g(x)|| ≤ ɛ is checked where ɛ is a gradient tolerance.
When optimality is not achieved, B is updated according to the BFGS formula
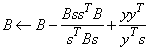
where s = xn − xc and y = gn − gc. Another search direction is then computed to begin the next iteration. For more details, see Dennis and Schnabel (1983, Appendix A).
In this implementation, the first stopping criterion for imsl_f_min_uncon_multivar occurs when the norm of the gradient is less than the given gradient tolerance grad_tol. The second stopping criterion for imsl_f_min_uncon_multivar occurs when the scaled distance between the last two steps is less than the step tolerance step_tol.
Since by default, a finite-difference method is used to estimate the gradient for some single precision calculations, an inaccurate estimate of the gradient may cause the algorithm to terminate at a noncritical point. In such cases, high precision arithmetic is recommended; the keyword IMSL_GRAD should be used to provide more accurate gradient evaluation.
On some platforms, imsl_f_min_uncon_multivar can evaluate the user-supplied functions fcn and grad in parallel. This is done only if the function imsl_omp_options is called to flag user-defined functions as thread-safe. A function is thread-safe if there are no dependencies between calls. Such dependencies are usually the result of writing to global or static variables
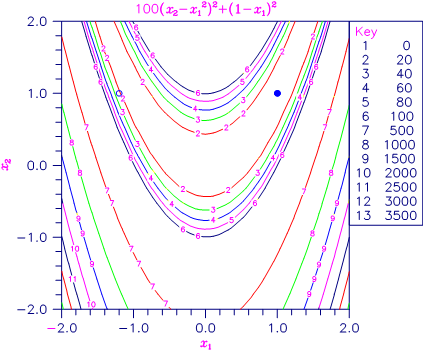
Figure 8- 1 Plot of the Rosenbrock Function
Examples
Example 1
The function
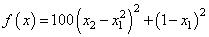
is minimized. In the following plot, the solid circle marks the minimum.
#include <stdio.h>
#include <imsl.h>
int main()
{
int i, n=2;
float *result, fx;
static float rosbrk(int, float[]);
imsl_omp_options(IMSL_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
/* Minimize Rosenbrock function */
result = imsl_f_min_uncon_multivar(rosbrk, n, 0);
fx = rosbrk(n, result);
/* Print results */
printf(" The solution is ");
for (i = 0; i < n; i++) printf("%8.3f", result[i]);
printf("\n\n The function value is %8.3f\n", fx);
} /* end of main */
static float rosbrk(int n, float x[])
{
float f1, f2;
f1 = x[1] - x[0]*x[0];
f2 = 1.0 - x[0];
return 100.0 * f1 * f1 + f2 * f2;
} /* end of function */
Output
The solution is 1.000 1.000
The function value is 0.000
Example 2
The function
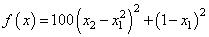
is minimized with the initial guess x = (−1.2, 1.0). The initial guess is marked with an open circle in the figure on page 20.
#include <stdio.h>
#include <imsl.h>
int main()
{
int i, n=2;
float *result, fx;
static float rosbrk(int, float[]);
static void rosgrd(int, float[], float[]);
static float xguess[2] = {-1.2e0, 1.0e0};
static float grad_tol = .0001;
imsl_omp_options(IMSL_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
/* Minimize Rosenbrock function using initial guesses of -1.2 and 1.0 */
result = imsl_f_min_uncon_multivar(rosbrk, n, IMSL_XGUESS, xguess,
IMSL_GRAD, rosgrd,
IMSL_GRAD_TOL, grad_tol,
IMSL_FVALUE, &fx, 0);
/* Print results */
printf(" The solution is ");
for (i = 0; i < n; i++) printf("%8.3f", result[i]);
printf("\n\n The function value is %8.3f\n", fx);
} /* End of main */
static float rosbrk(int n, float x[])
{
float f1, f2;
f1 = x[1] - x[0]*x[0];
f2 = 1.0e0 - x[0];
return 100.0 * f1 * f1 + f2 * f2;
} /* End of function */
static void rosgrd(int n, float x[], float g[])
{
g[0] = -400.0*(x[1]-x[0]*x[0])*x[0] - 2.0*(1.0-x[0]);
g[1] = 200.0*(x[1]-x[0]*x[0]);
} /* End of function */
Output
The solution is 1.000 1.000
The function value is 0.000
Informational Errors
|
IMSL_STEP_TOLERANCE |
Scaled step tolerance satisfied. The current point may be an approximate local solution, but it is also possible that the algorithm is making very slow progress and is not near a solution, or that step_tol is too big. |
Warning Errors
|
IMSL_TOO_MANY_ITN |
Maximum number of iterations exceeded. |
|
IMSL_TOO_MANY_FCN_EVAL |
Maximum number of function evaluations exceeded. |
|
IMSL_TOO_MANY_GRAD_EVAL |
Maximum number of gradient evaluations exceeded. |
|
IMSL_UNBOUNDED |
Five consecutive steps have been taken with the maximum step length. |
|
IMSL_NO_FURTHER_PROGRESS |
The last global step failed to locate a lower point than the current x value. |
Fatal Errors
|
IMSL_FALSE_CONVERGENCE |
False convergence—The iterates appear to be converging to a noncritical point. Possibly incorrect gradient information is used, or the function is discontinuous, or the other stopping tolerances are too tight. |

