Solves a sparse convex quadratic programming problem by an infeasible primal-dual interior-point method.

Synopsis

#include <imsl.h>

double *imsl_d_sparse_quadratic_prog (int m, int n, int nza, int nzq, Imsl_d_sparse_elem a[], double b[], double c[], Imsl_d_sparse_elem q[], …, 0)

Required Arguments

int m   (Input)
Number of constraints.

int n   (Input)
Number of variables.

int nza   (Input)
Number of nonzero entries in constraint matrix A.

int nzq (Input)
Number of nonzero entries in the lower triangular part of the matrix Q of the objective function.

Imsl_d_sparse_elem a[]   (Input)
An array of length nza containing the location and value of each nonzero coefficient in the constraint matrix A.

double b[]   (Input)
An array of length m containing the right-hand side of the constraints; if there are limits on both sides of the constraints, then b contains the lower limit of the constraints.

double c[]   (Input)
An array of length n containing the coefficients of the linear term of the objective function.

Imsl_d_sparse_elem q[]   (Input)
Array of length nzq containing the location and value of each nonzero coefficient in the lower triangular part of the matrix Q of the objective function. The matrix must be symmetric positive semidefinite.

Return Value

A pointer to an array of length n containing the solution x of the convex QP problem. To release this space, use imsl_free. If no solution can be computed, then NULL is returned.

Synopsis with Optional Arguments

#include <imsl.h>

double *imsl_d_sparse_quadratic_prog (int m, int n, int nza, int nzq, Imsl_d_sparse_elem a[], double b[], double c[], Imsl_d_sparse_elem q[],

IMSL_CONSTR_TYPE, int irtype[],

IMSL_UPPER_LIMIT, double bu[],

IMSL_LOWER_BOUND, double xlb[],

IMSL_UPPER_BOUND, double xub[],

IMSL_OBJ_CONSTANT, double c0,

IMSL_MAX_ITERATIONS, int max_iterations,

IMSL_OPT_TOL, double opt_tol,

IMSL_PRINF_TOL, double prinf_tol,

IMSL_DLINF_TOL, double dlinf_tol,

IMSL_PRINT, int iprint,

IMSL_PRESOLVE, int presolve,

IMSL_CSC_FORMAT, int a_colptr[], int a_rowind[], double a_values[], int q_colptr[], int q_rowind[], double q_values[],

IMSL_TERMINATION_STATUS, int *status,

IMSL_OBJ, double *obj,

IMSL_ITERATION_COUNT, int *iterations,

IMSL_DUAL, double **y,

IMSL_DUAL_USER, double y[],

IMSL_PRIMAL_INFEAS, double *err_b, double *err_u,

IMSL_DUAL_INFEAS, double *err_c,

IMSL_CP_RATIO_SMALLEST, double *cp_smallest,

IMSL_CP_RATIO_LARGEST, double *cp_largest,

IMSL_RETURN_USER, double x[],

0)

Optional Arguments

IMSL_CONSTR_TYPE, int irtype[]   (Input)
An array of length m indicating the types of general constraints in the matrix A. Let ri = ai1x1 + … + ainxn. Then, the value of irtype[i] signifies the following:

 

irtype[i]	Constraint
0	ri = bi
1	ri ≤ bi
2	ri ≥ bi
3	bi ≤ ri ≤ bui
4	Ignore this constraint

 

            Note that irtype[i] = 3 should only be used for constraints i with both finite lower and finite upper bound. For one-sided constraints, use irtype[i] = 1 or irtype[i] = 2. For free constraints, use irtype[i]  = 4.
Default: irtype = 0

IMSL_UPPER_LIMIT, double bu[]   (Input)
An array of length m containing the upper limit of the constraints that have both a lower and an upper bound. If such a constraint exists, then optional argument IMSL_CONSTR_TYPE must be used to define the type of constraints.  If irtype[i]≠ 3, i.e. if constraint i is not two-sided, then the corresponding entry in bu, bu[i], is ignored.
Default:  None of the constraints has an upper bound.

IMSL_LOWER_BOUND, double xlb[]   (Input)
An array of length n containing the lower bound on the variables. If there is no lower bound on a variable, then −1030 should be set as the lower bound.
Default:  xlb = 0.

IMSL_UPPER_BOUND, double xub[]   (Input)
An array of length n containing the upper bound on the variables. If there is no upper bound on a variable, then 1030 should be set as the upper bound.
Default:  None of the variables has an upper bound.

IMSL_OBJ_CONSTANT, double c0 (Input)
Value of the constant term in the objective function.
Default:  c0 = 0.

IMSL_MAX_ITERATIONS, int max_iterations (Input)
The maximum number of iterations allowed for the primal-dual solver.
Default:  max_iterations = 200.

IMSL_OPT_TOL, double opt_tol (Input)
Relative optimality tolerance.
Default:  opt_tol = 1.0e-10.

IMSL_PRINF_TOL, double prinf_tol (Input)
The primal infeasibility tolerance.
Default:  prinf_tol = 1.0e-8.

IMSL_DLINF_TOL, double dlinf_tol (Input)
The dual infeasibility tolerance.
Default:  dlinf_tol = 1.0e-8.

IMSL_PRINT, int iprint (Input)
Printing option.

 

iprint	Action
0	No printing is performed.
1	Prints statistics on the QP problem and the solution process.

 

            Default:  iprint = 0.

IMSL_PRESOLVE, int presolve  (Input)
Presolve the QP problem in order to reduce the problem size or to detect infeasibility or unboundedness of the problem. Depending on the number of presolve techniques used different presolve levels can be chosen:

 

presolve	Description
0	No presolving.
1	Eliminate singleton rows
2	Additionally to 1, eliminate redundant (and forcing) rows.
3	Additionally to 2, eliminate dominated variables.
4	Additionally to 3, eliminate singleton columns.
5	Additionally to 4, eliminate doubleton rows.
6	Additionally to 5, eliminate aggregate columns.

 

            Default:  presolve = 0.

IMSL_CSC_FORMAT, int a_colptr[], int a_rowind[], double a_values[], int q_colptr[], int q_rowind[], double q_values[]   (Input)
Accept the constraint matrix A (via vectors a_colptr, a_rowind and a_values) and the matrix Q of the objective function (via vectors q_colptr, q_rowind and q_values) in Harwell-Boeing (CSC) format. See the main “Introduction” chapter of this manual for a discussion of this storage scheme.

     If this optional argument is used, then required arguments a and q are ignored.

IMSL_TERMINATION_STATUS, int *status (Output)
The termination status for the problem.

 

status	Description
0	Optimal solution found.
1	The problem is primal infeasible (or dual unbounded).
2	The problem is primal unbounded (or dual infeasible).
3	Suboptimal solution found (accuracy problems).
4	Iterations limit max_iterations exceeded.

 

IMSL_OBJ, double *obj   (Output)
Optimal value of the objective function.

IMSL_ITERATION_COUNT, int *iterations   (Output)
The number of iterations required by the primal-dual solver.

IMSL_DUAL, double **y   (Output)
The address of a pointer y to an internally allocated array of length m containing the dual solution.

IMSL_DUAL_USER, double y[]   (Output)
A user-allocated array of size m containing the dual solution.

IMSL_PRIMAL_INFEAS, double *err_b, double *err_u   (Output)
The violation of the primal constraints, described by err_b, the primal infeasibility of the solution, and by err_u, the violation of the variable bounds.

IMSL_DUAL_INFEAS, double *err_c   (Output)
The violation of the dual constraints, described by err_c, the dual infeasibility of the solution.

IMSL_CP_RATIO_SMALLEST, double *cp_smallest   (Output)
The ratio of the smallest complementarity product to the average.

IMSL_CP_RATIO_LARGEST, double *cp_largest   (Output)
The ratio of the largest complementarity product to the average.

IMSL_RETURN_USER, double x[]   (Output)
A user-allocated array of length n containing the primal solution.

Description

The function imsl_d_sparse_quadratic_prog uses an infeasible primal-dual interior-point method to solve convex quadratic programming problems, i.e., problems of the form

where  c is the objective coefficient vector, Q is the symmetric positive semidefinite coefficient matrix, A is the constraint matrix and the vectors bl, bu, xl, and xu are the lower and upper bounds on the constraints and the variables, respectively.

Internally, imsl_d_sparse_quadratic_prog transforms the problem given by the user into a simpler form that is computationally more tractable. After redefining the notation, the new form reads

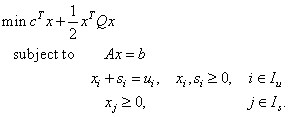
Here, 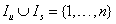is a partition of the index set 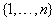into upper bounded and standard variables.

In order to simplify the description it is assumed in the following that the problem above contains only variables with upper bounds, i.e. is of the form

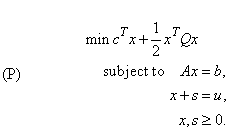
The corresponding dual problem is then

The Karush-Kuhn-Tucker (KKT) optimality conditions for (P) and (D) are

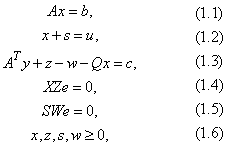
where 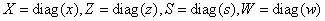are diagonal matrices and 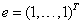 is a vector of ones.

Function imsl_d_sparse_quadratic_prog, like all infeasible interior point methods, generates a sequence

    

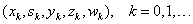
of iterates, that satisfy 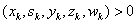  for all 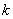, but are in general not feasible, i.e. the linear constraints (1.1)-(1.3) are only satisfied in the limiting case .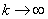

The barrier parameter 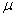, defined by

,

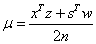measures how good the complementarity conditions (1.4), (1.5) are satisfied.

Mehrotra’s predictor-corrector algorithm is a variant of Newton’s method applied to the KKT conditions (1.1)-(1.5). Function imsl_d_sparse_quadratic_prog uses a modified version of this algorithm to compute the iterates 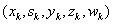. In every step of the algorithm, the search direction vector

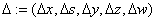
is decomposed into two parts, 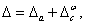where 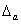 and 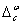denote the affine-scaling and a weighted centering component, respectively. Here,

,

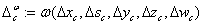where the scalar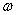denotes the corrector weight.

The vectors 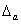and 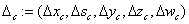are determined by solving the linear system

for two different right-hand sides.

For 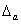, the right-hand side is defined as

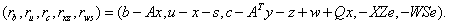
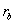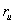Here,  and  are the violations of the primal constraints and 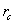defines the violations of the dual constraints.

The resulting direction 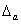 is the pure Newton step applied to the system (1.1)-(1.5).

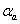In order to obtain the corrector direction , the maximum stepsize  in the primal and dual space preserving nonnegativity of 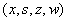, is determined and the predicted complementarity gap

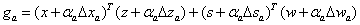
is computed. It is then used to determine the barrier parameter

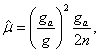
where  denotes the current complementarity gap.

The direction is then computed by choosing

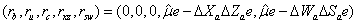
as the right-hand side in the linear system (2).

Function imsl_d_sparse_quadratic_prog now uses a linesearch to find the optimal weight 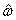 that maximizes the stepsize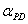in the primal and dual direction of .

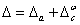A new iterate is then computed using a step reduction factor :

.

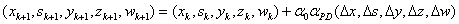In addition to the weighted Mehrotra predictor-corrector, imsl_d_sparse_quadratic_prog also uses multiple centrality correctors to enlarge the primal-dual stepsize per iteration step and to reduce the overall number of iterations required to solve a QP problem. The maximum number of centrality corrections depends on the ratio of the factorization and solve efforts for system (2) and is therefore problem dependent. For a detailed description of multiple centrality correctors, refer to Gondzio(1994).

The linear system (2) can be reduced to more compact forms, the augmented system (AS)

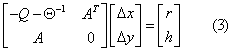
or further by elimination of 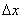to the normal equations (NE) system

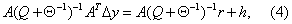
where

,   ,   .

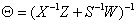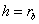The matrix on the left-hand side of (3), which is symmetric indefinite, can be transformed into a symmetric quasidefinite matrix by regularization. Since these types of matrices allow for a Cholesky-like factorization, the resulting linear system can be solved easily for 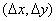 by triangular substitutions.  For more information on the regularization technique, see Altman and Gondzio (1998). For the NE system, matrix 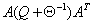is positive definite, and therefore a sparse Cholesky algorithm can be used to factor 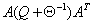and solve the system for 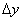by triangular substitutions with the Cholesky factor .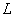

In function imsl_d_sparse_quadratic_prog, both approaches are implemented. The AS approach is chosen if 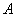 contains dense columns, if there is a considerable number of columns in 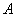 that are much denser than the remaining ones or if there are many more rows than columns in the structural part of 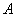. Otherwise, the NE approach is selected.

Function imsl_d_sparse_quadratic_prog stops with optimal termination status if the current iterate satisfies the following three conditions:

,

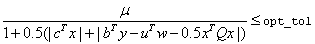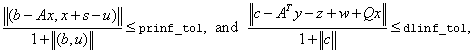
where prinf_tol, dlinf_tol and opt_tol are primal infeasibility, dual infeasibility and optimality tolerances, respectively. The default value is 1.0e-10 for opt_tol and 1.0e-8 for the two other tolerances.

Function imsl_d_sparse_quadratic_prog is based on the code HOPDM developed by Jacek Gondzio et al., see the HOPDM User’s Guide (1995).

Examples

Example 1

The convex quadratic programming problem

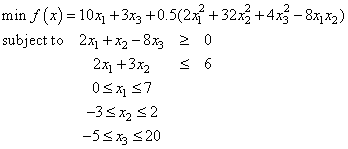
is solved.

 

#include <imsl.h>

#include <stdio.h>

 

int main()

{

    int m = 2, n = 3, nza = 5, nzq = 4;

    Imsl_d_sparse_elem a[] = { 0, 0, 2.0,

        0, 1, 1.0,

        0, 2, -8.0,

        1, 0, 2.0,

        1, 1, 3.0 };

 

    Imsl_d_sparse_elem q[] = { 0, 0, 2.0,

        1, 1, 32.0,

        2, 2, 4.0,

        1, 0, -4.0 };

 

    double b[] = { 0.0, 6.0 };

    double c[] = { 10.0, 0.0, 3.0 };

 

    double xlb[] = { 0.0, -3.0, -5.0 };

    double xub[] = { 7.0, 2.0, 20.0 };

 

    int irtype[] = { 2, 1 };

    double *x = NULL;

    double obj;

 

    x = imsl_d_sparse_quadratic_prog(m, n, nza, nzq, a, b, c, q,

        IMSL_CONSTR_TYPE, irtype,

        IMSL_LOWER_BOUND, xlb,

        IMSL_UPPER_BOUND, xub,

        IMSL_OBJ, &obj,

        0);

 

    imsl_d_write_matrix("x", 1, n, x, 0);

    printf("\nObjective: %lf\n", obj);

}

Output

 

                  x

          1            2            3

       0.00         0.00        -0.75

 

Objective: -1.125000

Example 2

This example demonstrates how the function imsl_d_read_mps can be used with imsl_d_sparse_quadratic_prog to solve a convex quadratic programming problem defined in an MPS file.  The MPS file used in this example is the file ‘qafiro’, available from the QP problems collection QPDATA2 on István Maros’ home page under http://www.doc.ic.ac.uk/~im/#DATA/ .

 

#include <imsl.h>

#include <stdio.h>

#include <stdlib.h>

 

int main()

{

    Imsl_d_mps  *problem;

    int          i, m, n, *irtype, nza, nzq;

    double  *x, objective, *bl, *bu, *xlb, *xub;

    Imsl_d_sparse_elem *a = NULL, *q = NULL;

 

    /* Read the QPS file. */

    problem = imsl_d_read_mps("QAFIRO.QPS", 0);

 

    m = problem->nrows;

    n = problem->ncolumns;

 

    /*

     * Setup the constraint matrix.

     */

    nza = problem->nonzeros;

    a = problem->constraint;

 

    /*

     * Setup the Hessian.

     */

    nzq = problem->nhessian;

    q = problem->hessian;

 

    /*

     * Setup constraint bounds and constraint type array.

     */

    irtype = (int*) malloc(m*sizeof(int));

    bl = (double*) malloc(m*sizeof(double));

    bu = (double*) malloc(m*sizeof(double));

 

    for (i = 0; i < m; i++) {

      if (problem->lower_range[i] == problem->negative_infinity &&

        problem->upper_range[i] == problem->positive_infinity)

      {

          bl[i] = problem->negative_infinity;

          bu[i] = problem->positive_infinity;

          irtype[i] = 4;

      }

      else if (problem->lower_range[i] == problem->negative_infinity)

      {

          irtype[i] = 1;

          bl[i] = problem->upper_range[i];

          bu[i] = problem->positive_infinity;

      }

      else if (problem->upper_range[i] == problem->positive_infinity)

      {

          irtype[i] = 2;

          bl[i] = problem->lower_range[i];

          bu[i] = problem->positive_infinity;

      }

      else

      {

        if (problem->lower_range[i] == problem->upper_range[i])

        {

          irtype[i] = 0;

          bl[i] = problem->lower_range[i];

          bu[i] = problem->positive_infinity;

        }

        else

        {

          irtype[i] = 3;

          bl[i] = problem->lower_range[i];

          bu[i] = problem->upper_range[i];

        }

      }

    }

 

    /*

     * Setup variable bounds.  Be sure to account for

     * how unbounded variables should be set.

     */

    xlb = (double*) malloc(n*sizeof(double));

    xub = (double*) malloc(n*sizeof(double));

 

    for (i = 0; i < n; i++) {

      xlb[i] = (problem->lower_bound[i] == problem->negative_infinity)?

                -1.0e30:problem->lower_bound[i];

      xub[i] = (problem->upper_bound[i] == problem->positive_infinity)?

                1.0e30:problem->upper_bound[i];

    }

 

    /*

     * Solve the QP problem.

     */

    x = imsl_d_sparse_quadratic_prog(m, n, nza, nzq,

        a, bl, problem->objective, q,

        IMSL_UPPER_LIMIT, bu,

        IMSL_CONSTR_TYPE, irtype,

        IMSL_LOWER_BOUND, xlb,

        IMSL_UPPER_BOUND, xub,

        IMSL_OBJ, &objective,

        IMSL_PRESOLVE, 6,

        0);

 

    /*

     * Output results.

     */

    printf("Problem Name: %s\n", problem->name);

    printf("objective   : %15.10e\n", objective);

    imsl_d_write_matrix("Solution", 1, n, x, 0);

 

    /*

     * Free memory.

     */

    imsl_d_mps_free(problem);

    imsl_free(irtype);

    imsl_free(bl);

    imsl_free(bu);

    imsl_free(xlb);

    imsl_free(xub);

    imsl_free(x);

}

Output

 

Problem Name: AFIRO

objective   : -1.5907817909e+000

 

                                  Solution

          1            2            3            4            5            6

       0.38         0.00         0.38         0.40        65.17         0.00

 

          7            8            9           10           11           12

       0.00         0.00         0.00         0.00         0.00         0.00

 

         13           14           15           16           17           18

       0.00        65.17        69.08         3.49         3.37         0.11

 

         19           20           21           22           23           24

       0.00         1.50        12.69         0.00         0.00         0.00

 

         25           26           27           28           29           30

       0.00         0.00         0.00         0.00         2.41        33.72

 

         31           32

       5.46         0.00

 

Warning Errors

 

IMSL_SUBOPTIMAL_SOL_FOUND	A suboptimal solution was found after # iterations.
IMSL_MAX_ITERATIONS_REACHED_1	The maximum number of iterations was reached. The best answer will be returned.  “#” = # was used, a larger value may help complete the algorithm.

 

Fatal Errors

 

IMSL_PRIMAL_UNBOUNDED	The primal problem is unbounded.
IMSL_PRIMAL_INFEASIBLE	The primal problem is infeasible.
IMSL_DUAL_INFEASIBLE	The dual problem is infeasible.
IMSL_INIT_SOL_INFEASIBLE	The initial solution for the one-row linear program is infeasible.
IMSL_PROB_UNBOUNDED	The problem is unbounded.
IMSL_DIAG_WEIGHT_TOO_SMALL	The diagonal element # [#] = # of the diagonal weight matrix # is too small.
IMSL_CHOL_FAC_ACCURACY	The Cholesky factorization failed because of accuracy problems.

---

Contact Support