Evaluates the Student’s t cumulative distribution function (CDF).
Synopsis
#include <imsl.h>
float imsl_f_t_cdf (float t, float df)
The type double function is imsl_d_t_cdf.
Required Arguments
float t
(Input)
Argument for which the Student’s t cumulative distribution
function is to be evaluated.
float df
(Input)
Degrees of freedom. Argument df must be greater
than or equal to 1.0.
Return Value
The probability that a Student’s t random variable takes a value less than or equal to the input t.
Description
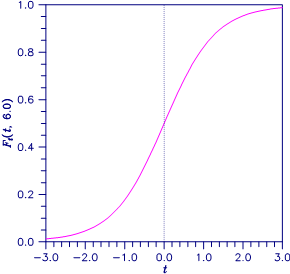
Function imsl_f_t_cdf evaluates the cumulative distribution function of a Student’s t random variable with ν = df degrees of freedom. If t2 ≥ ν, the following identity relating the Student’s t cumulative distribution function TCDF(t, ν) to the incomplete beta ratio function Ix (a, b) is used:
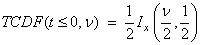
where
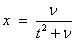
and
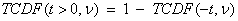
If t2 < ν, the solution
space is partitioned into four algorithms as follows: If ν ≥ 64 and t2 / ν ≤ 0.1,
a Cornish-Fisher expansion is used to evaluate the distribution function.
If ν < 64
and an integer and |t| < 2.0, a trigonometric series is used
(see Abramowitz and Stegun 1964, Equations 26.7.3 and 26.7.4 with some
rearrangement). If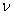 
< 64 and an integer and
|t| > 2.0, a series given by Hill (1970) that
converges well for large values of t is used. For the remaining
t2 < ν cases,
TCDF(t, ν) is
calculated using the identity:
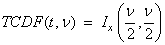
where
.
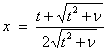Figure 9-2 Plot of Ft (t, 6.0)
Example
This example finds the probability that a t random variable with 6 degrees of freedom is greater in absolute value than 2.447. The fact that t is symmetric about 0 is used.
#include <imsl.h>
#include <stdio.h>
int main ()
{
float t = 2.447, df = 6.0, p;
p = 2.0*imsl_f_t_cdf(-t,df);
printf("Pr(|t(%1.0f)| > %5.3f) = %6.4f\n", df, t, p);
}
Output
Pr(|t(6)| > 2.447) = 0.0500
