Finds the real zeros of a real, continuous, univariate function.
Synopsis
#include <imsl.h>
float *imsl_f_zeros_function (float fcn(), …, 0)
The type double function is imsl_d_zeros_function.
Required Arguments
float fcn (float x)
(Input/Output)
User-supplied function to compute the value of the function of
which the zeros will be found.
float x
(Input)
The point at which the function is evaluated.
Return Value
The
computed function value at the point x.
Return Value
A pointer to an array containing the zeros of the function. The zeros are in increasing order. If fewer than the requested number of zeros were found, the final entries are set to NaN. To release this space, use imsl_free. If there is a fatal error, then NULL is returned.
Synopsis with Optional Arguments
#include <imsl.h>
float *imsl_f_zeros_function (float fcn(),
IMSL_NUM_ROOTS, int num_roots,
IMSL_FCN_W_DATA, float fcn(), void *data,
IMSL_NUM_ROOTS_FOUND, int *num_roots_found,
IMSL_N_EVALS, int *n_evals,
IMSL_BOUND, float a, float b,
IMSL_MAX_EVALS, int max_evals,
IMSL_XGUESS, float xguess[],
IMSL_ERR_ABS, float err_abs,
IMSL_ERR_X, float err_x,
IMSL_TOLERANCE_MULLER, float tolerance_muller,
IMSL_MIN_SEPARATION, float min_separation,
IMSL_XSCALE, float xscale,
IMSL_RETURN_USER, float x[],
0)
Optional Arguments
IMSL_NUM_ROOTS, int num_roots
(Input)
The number of zeros to be found.
Default: num_roots = 1.
IMSL_FCN_W_DATA, float fcn (float x, void *data),
void *data (Input)
User
supplied function to compute the value of the function of which the zeros will
be found, which also accepts a pointer to data that is supplied by the user. See
the Introduction, Passing
Data to User-Supplied Functions at the beginning of this manual for more
details.
float x
(Input)
The point at which the function is evaluated.
void *data
(Input)
A pointer to the data to be passed to the user-supplied function.
Return Value
The
computed function value at the point x.
IMSL_NUM_ROOTS_FOUND, int *num_roots_found
(Output)
The number of zeros actually found.
IMSL_N_EVALS, int *n_evals
(Output)
The actual number of function evaluations used.
IMSL_BOUND, float a, float b
(Input)
The closed interval in which to search for the roots. The function
must be defined for all values in this interval.
Default: The search for the
roots is not bounded.
IMSL_MAX_EVALS, int max_evals
(Input)
The maximum number of function evaluations allowed. Once this limit
is reached, the roots found are returned.
Default: max_evals = 100
IMSL_XGUESS, float xguess[]
(Input)
Array with num_roots
components containing initial guesses for the zeros. If a bound on the zeros is
also given, the guesses must satisfy the bound condition.
IMSL_ERR_ABS, float err_abs
(Input)
A convergence criterion. A root is accepted if the absolute value of
the function at the point is less than or equal to err_abs.
Default:
err
_abs= 100 ɛ, where ɛ is the machine
precision.
IMSL_ERR_X, float err_x
(Input)
A convergence criterion. A root is accepted if it is
bracketed within an interval of length err_x.
Default:
err_x = 100 ɛ / xscale, where ɛ is the machine
precision.
IMSL_TOLERANCE_MULLER, float tolerance_muller
(Input)
Müller’s method is started if, during refinement, a point is found
for which the absolute value of the function is less than tolerance_muller and
the point is not near an already discovered root. If tolerance_muller is
less than or equal to zero Müller’s method is never used.
Default: tolerance_muller = ɛ / err_abs, where ɛ is the machine
precision. With the default value of err_abs, this equals
0.01.
IMSL_MIN_SEPARATION, float min_separation
(Input)
The minimum separation between accepted roots. If two points both
satisfy the convergence criteria, but are within min_separation of each
other, only one of the roots is accepted.
Default: min_separation = ɛ1/2/xscale, where ɛ is the machine
precision.
IMSL_XSCALE, float xscale
(Input)
The scaling in the x-coordinate. The absolute value of the
roots divided by xscale should be about
one.
Default: xscale = 1.0
IMSL_RETURN_USER, float x[]
(Output)
Array with num_root components
containing the computed zeros.
Description
The function imsl_f_zeros_function computes num_roots real zeros of a real, continuous, univariate function. The search for the zeros of the function can be limited to a specified interval, or extended over the entire real line. The code is generally more efficient if an interval is specified. The user supplied function must return valid results for all values in the specified interval. If no interval is given, the user-supplied function must return valid results for all real numbers.
The function has two convergence criteria. The first criterion accepts a root, x, if
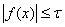
where τ = err_x.
The second criterion accepts a root if it is known to be inside of an interval of length at most err_abs.
A root is accepted if it satisfies either criteria and is not within min_separation of another accepted root.
If initial guesses for the roots are given, Müller’s method (Müller 1956) is used for each of these guesses. For each guess, the Müller iteration is stopped if the next step would be outside of the bound, if given. The iteration is also stopped if it cannot make further progress in finding a root.
If no guess for the zeros were given, or if Müller’s method with the guesses did not find the requested number of roots, a meta-algorithm, combining Müller’s and Brent’s methods, is used. Müller’s method is used primarily to find the roots of functions, such as f(x) = x2, where the function does not cross the y=0 line. Brent’s method is used to find other types of roots.
The meta-algorithm successively refines the interval using a one-dimensional Faure low-discrepancy sequence. If the optional argument IMSL_BOUND is used to specify a bounded interval, [a,b], the Faure sequence is scaled from (0,1) to (a,b).
If no bound on the function’s domain is given, the entire real line must be searched for roots. In this case the Faure sequence is scaled from (0, 1) to (-∞,+∞) using the mapping
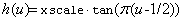
where xscale is given by the optional argument IMSL_XSCALE.
At each step of the iteration the next point in the Faure sequence is added to the list of breakpoints defining the subintervals. Call the points x0=a, x1=b, x2, x3, …. The new point, xs splits an existing subinterval, [xp, xq].
The function is evaluated at xs. If its value is small enough, specifically if
then Müller’s method is used with xp, xq and xs as starting values. If a root is found, it is added to the list of roots. If more roots are required, the new Faure point is used.
If Müller’s method did not find a root using the new point,
the function value at the point is compared with the function values at the
endpoints of the subinterval it divides. If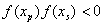 
and no root has previously been found in
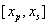then Brent’s method is used to find a
root in this interval. Similarly, if the function changes sign over the
interval
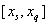, and a root has not already been found
in the subinterval, Brent’s method is used there.
Examples
Example 1
This example finds a real zero of the function.
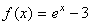
#include <imsl.h>
#include <math.h>
#include <stdio.h>
float fcn(float x);
int main()
{
float *x;
x = imsl_f_zeros_function (fcn, 0);
printf("fcn(%6.3f) = %12.3e\n",
x[0], fcn(x[0]));
}
float fcn(float x)
{
return exp(x) - 3.0;
}
Output
fcn( 1.099) = -6.378e-006
Example 2
This example finds two real zeros of function
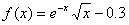
on the interval [0,20].
#include <imsl.h>
#include <math.h>
float fcn(float x);
int main()
{
float *x;
int n_found;
x = imsl_f_zeros_function (fcn,
IMSL_NUM_ROOTS, 2,
IMSL_BOUND, 0.0, 20.0,
IMSL_NUM_ROOTS_FOUND, &n_found,
0);
imsl_f_write_matrix ("x", 1, n_found, x, 0);
}
float fcn(float x)
{
return sqrt(x)*exp(-x) - 0.3;
}
Output
x
1 2
0.113 1.356
Warning Errors
IMSL_ZEROS_MAX_EVALS_EXCEEDED The maximum number of function evaluations allowed has been exceeded. Any zeros found are returned.
