Computes the sample autocorrelation function of a stationary time series.
Synopsis
float *imsls_f_autocorrelation (int n_observations, float x[], int lagmax, ...0)
The type double function is imsls_d_autocorrelation.
Required Arguments
int n_observations
(Input)
Number of observations in the time series x. n_observations must be
greater than or equal to 2.
float x[]
(Input)
Array of length n_observations
containing the time series.
int lagmax (Input)
Maximum lag of autocovariance, autocorrelations, and standard errors of
autocorrelations to be computed. lagmax must be greater
than or equal to 1 and less than n_observations.
Return Value
Pointer to an array of length lagmax + 1 containing the autocorrelations of the time series x. The 0-th element of this array is 1. The k-th element of this array contains the autocorrelation of lag k where k = 1, ..., lagmax.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_autocorrelation (int
n_observations,
float x[],
int lagmax,
IMSLS_PRINT_LEVEL,
int iprint,
IMSLS_X_MEAN_IN,
float x_mean_in,
IMSLS_X_MEAN_OUT,
float *x_mean_out,
IMSLS_ACV,
float **autocovariances,
IMSLS_ACV_USER,
float autocovariances[],
IMSLS_SEAC,
float **standard_errors, int
se_option,
IMSLS_SEAC_USER, float standard_errors[],
int
se_option,
IMSLS_RETURN_USER,
float autocorrelations[],
0)
Optional Arguments
IMSLS_PRINT_LEVEL,
int iprint
(Input)
Printing option.
Default = 0.
|
iprint |
Action |
|
0 |
No printing is performed. |
|
1 |
Prints the mean and variance. |
|
2 |
Prints the mean, variance, and autocovariances. |
|
3 |
Prints the mean, variance, autocovariances, autocorrelations, and standard errors of autocorrelations. |
IMSLS_X_MEAN_IN,
float x_mean_in
(Input)
User input the estimate of the time series x.
IMSLS_X_MEAN_OUT,
float *x_mean_out
(Output)
If specified, x_mean_out is the
estimate of the mean of the time
series x.
IMSLS_ACV,
float **autocovariances
(Output)
Address of a pointer to an array of length lagmax + 1 containing
the variance and autocovariances of the time series x. The
0-th element of this array is the variance of the time series x. The
kth element contains the autocovariance of lag k
where k = 1, ..., lagmax.
IMSLS_ACV_USER,
float autocovariances[]
(Output)
If specified, autocovariances is an
array of length lagmax + 1
containing the variance and autocovariances of the time series x.
See IMSLS_ACV.
IMSLS_SEAC,
float **standard_errors,
int se_option
(Output)
Address of a pointer to an array of length lagmax containing the
standard errors of the autocorrelations of the time series x.
Method of
computation for standard errors of the autocorrelations is chosen by se_option.
|
se_option |
Action |
|
1 |
Compute the standard errors of autocorrelations using Barlett’s formula. |
|
2 |
Compute the standard errors of autocorrelations using Moran’s formula. |
IMSLS_SEAC_USER,
float standard_errors[],
int se_option
(Output)
If specified, autocovariances is an
array of length lagmax containing the
standard errors of the autocorrelations of the time series x.
See IMSLS_SEAC.
IMSLS_RETURN_USER,
float autocorrelations[]
(Output)
If specified, autocorrelations is an array of length lagmax + 1 containing
the autocorrelations of the time series x. The oth element of this array
is 1. The kth element of this array contains the autocorrelation of
lag k where k = 1, ..., lagmax.
Description
Function imsls_f_autocorrelation estimates the autocorrelation function of a stationary time series given a sample of n = n_observations observations {Xt} for t = 1, 2, …, n.
Let
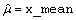
be the estimate of the mean μ of the time series {Xt} where
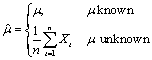
The autocovariance function σ(k) is estimated by
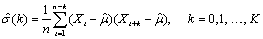
where K = lagmax. Note that
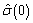
is an estimate of the sample variance. The autocorrelation function ρ(k) is estimated by
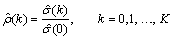
Note that
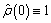
by definition.
The standard errors of the sample autocorrelations may be optionally computed according to argument se_option for the optional argument IMSLS_SEAC. One method (Bartlett 1946) is based on a general asymptotic expression for the variance of the sample autocorrelation coefficient of a stationary time series with independent, identically distributed normal errors. The theoretical formula is
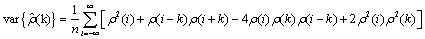
where
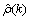
assumes μ is unknown. For computational purposes, the autocorrelations r(k) are replaced by their estimates
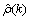
for |k| ≤ K, and the limits of summation are bounded
because of the assumption that
r(k) = 0 for all k such that |k| > K.
A second method (Moran 1947) utilizes an exact formula for the variance of the sample autocorrelation coefficient of a random process with independent, identically distributed normal errors. The theoretical formula is
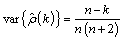
where μ is assumed to be equal to zero. Note that this formula does not depend on the autocorrelation function.
Example
Consider the Wolfer Sunspot Data (Anderson 1971, page 660) consisting of the number of sunspots observed each year from 1749 through 1924. The data set for this example consists of the number of sunspots observed from 1770 through 1869. Function imsls_f_autocorrelation with optional arguments computes the estimated autocovariances, estimated autocorrelations, and estimated standard errors of the autocorrelations.
#include <imsls.h>
#include <stdio.h>
int main()
{
float *result=NULL, data[176][2], x[100], xmean;
int i, nobs = 100, lagmax = 20;
float *acv=NULL, *seac=NULL;
imsls_f_data_sets(2, IMSLS_RETURN_USER, data, 0);
for (i=0;i<nobs;i++) x[i] = data[21+i][1];
result = imsls_f_autocorrelation(nobs, x, lagmax,
IMSLS_X_MEAN_OUT, &xmean,
IMSLS_ACV, &acv,
IMSLS_SEAC, &seac, 1,
0);
printf("Mean = %8.3f\n", xmean);
printf("Variance = %8.1f\n", acv[0]);
printf("\nLag\t ACV\t\t AC\t\t SEAC\n");
printf("%2d\t%8.1f\t%8.5f\n", 0, acv[0], result[0]);
for(i=1; i<21; i++)
printf("%2d\t%8.1f\t%8.5f\t%8.5f\n", i, acv[i], result[i],
seac[i-1]);
}
Output
Mean = 46.976
Variance = 1382.9
Lag ACV AC SEAC
0 1382.9 1.00000
1 1115.0 0.80629 0.03478
2 592.0 0.42809 0.09624
3 95.3 0.06891 0.15678
4 -236.0 -0.17062 0.20577
5 -370.0 -0.26756 0.23096
6 -294.3 -0.21278 0.22899
7 -60.4 -0.04371 0.20862
8 227.6 0.16460 0.17848
9 458.4 0.33146 0.14573
10 567.8 0.41061 0.13441
11 546.1 0.39491 0.15068
12 398.9 0.28848 0.17435
13 197.8 0.14300 0.19062
14 26.9 0.01945 0.19549
15 -77.3 -0.05588 0.19589
16 -143.7 -0.10394 0.19629
17 -202.0 -0.14610 0.19602
18 -245.4 -0.17743 0.19872
19 -230.8 -0.16691 0.20536
20 -142.9 -0.10332 0.20939
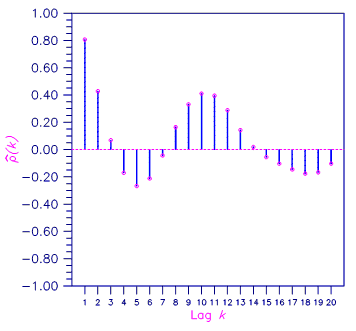
Figure 8-1 Sample Autocorrelation Function

