Performs a forward or an inverse Box-Cox (power) transformation.
Synopsis
#include <imsls.h>
float *imsls_f_box_cox_transform (int n_observations, float z[], float power, ..., 0)
The type double function is imsls_d_box_cox_transform.
Required Arguments
int
n_observations (Input)
Number of observations in z.
float z[]
(Input)
Array of length n_observations
containing the observations.
float power
(Input)
Exponent parameter in the Box-Cox (power) transformation.
Return Value
Pointer to an internally allocated array of length n_observations containing the transformed data. To release this space, use imsls_free. If no value can be computed, then NULL is returned.
Synopsis with Optional Arguments
#include <imsls.h>
float
*imsls_f_box_cox_transform (int
n_observations,
float z[],
float power,
IMSLS_SHIFT,
float shift,
IMSLS_INVERSE_TRANSFORM,
IMSLS_RETURN_USER,
float x[],
0)
Optional Arguments
IMSLS_SHIFT, float shift
(Input)
Shift parameter in the Box-Cox (power) transformation. Parameter
shift must satisfy the relation min (z(i)) + shift > 0.
Default:
shift = 0.0.
IMSLS_INVERSE_TRANSFORM
If
IMSLS_INVERSE_TRANSFORM
is specified, the inverse transform is performed.
IMSLS_RETURN_USER, float x[]
(Output)
User-allocated array of length n_observations
containing the transformed data.
Description
Function imsls_f_box_cox_transform performs a forward or an inverse Box-Cox (power) transformation of n = n_observations observations {Zt} for t = 1, 2, ..., n.
The forward transformation is useful in the analysis of linear models or models with nonnormal errors or nonconstant variance (Draper and Smith 1981, p. 222). In the time series setting, application of the appropriate transformation and subsequent differencing of a series can enable model identification and parameter estimation in the class of homogeneous stationary autoregressive-moving average models. The inverse transformation can later be applied to certain results of the analysis, such as forecasts and prediction limits of forecasts, in order to express the results in the scale of the original data. A brief note concerning the choice of transformations in the time series models is given in Box and Jenkins (1976, p. 328).
The class of power transformations discussed by Box and Cox (1964) is defined by
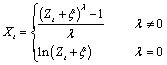
where Zt + ξ > 0 for all t. Since
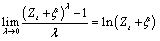
the family of power transformations is continuous.
Let λ = power and ξ = shift; then, the computational formula used by imsls_f_box_cox_transform is given by
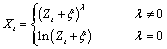
where Zt + ξ > 0 for all t. The computational and Box-Cox formulas differ only in the scale and origin of the transformed data. Consequently, the general analysis of the data is unaffected (Draper and Smith 1981, p. 225).
The inverse transformation is computed by
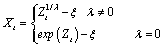
where {Zt} now represents the result computed by imsls_f_box_cox_transform for a forward transformation of the original data using parameters λ and ξ.
Examples
Example 1
The following example performs a Box-Cox transformation with power = 2.0 on 10 data points.
#include <imsls.h>
int main() {
int n_observations = 10;
float power = 2.0;
float *x;
static float z[10] ={
1.0, 2.0, 3.0, 4.0, 5.0, 5.5, 6.5, 7.5, 8.0, 10.0};
/* Transform Data using Box Cox Transform */
x = imsls_f_box_cox_transform(n_observations, z, power, 0);
imsls_f_write_matrix("Transformed Data", 1, n_observations, x, 0);
imsls_free(x);
}
Output
Transformed Data
1 2 3 4 5 6
1.0 4.0 9.0 16.0 25.0 30.2
7 8 9 10
42.2 56.2 64.0 100.0
Example 2
This example extends the first example—an inverse transformation is applied to the transformed data to return to the orignal data values.
#include <imsls.h>
int main() {
int n_observations = 10;
float power = 2.0;
float *x, *y;
static float z[10] ={
1.0, 2.0, 3.0, 4.0, 5.0, 5.5, 6.5, 7.5, 8.0, 10.0};
/* Transform Data using Box Cox Transform */
x = imsls_f_box_cox_transform(n_observations, z, power, 0);
imsls_f_write_matrix("Transformed Data", 1, n_observations, x, 0);
/* Perform an Inverse Transform on the Transformed Data */
y = imsls_f_box_cox_transform(n_observations, x, power,
IMSLS_INVERSE_TRANSFORM, 0);
imsls_f_write_matrix("Inverse Transformed Data", 1, n_observations,
y, 0);
imsls_free(x);
imsls_free(y);
}
Output
Transformed Data
1 2 3 4 5 6
1.0 4.0 9.0 16.0 25.0 30.2
7 8 9 10
42.2 56.2 64.0 100.0
Inverse Transformed Data
1 2 3 4 5 6
1.0 2.0 3.0 4.0 5.0 5.5
7 8 9 10
6.5 7.5 8.0 10.0
Fatal Errors
IMSLS_ILLEGAL_SHIFT “shift” = # and the smallest element of “z” is “z[#]” = #. “shift” plus “z[#]” = #. “shift” + “z[i]” must be greater than 0 for i = 1, ..., “n_observations”. “n_observations” = #.
IMSLS_BCTR_CONTAINS_NAN One or more elements of “z” is equal to NaN (Not a number). No missing values are allowed. The smallest index of an element of “z” that is equal to NaN is #.
IMSLS_BCTR_F_UNDERFLOW Forward transform. “power” = #. “shift” = #. The minimum element of “z” is “z[#]” = #. (“z[#]”+ “shift”) ^ “power” will underflow.
IMSLS_BCTR_F_OVERFLOW Forward transformation. “power” = #. “shift” = #. The maximum element of “z” is “z[#]” = #. (“z[#]” + “shift”) ^ “power” will overflow.
IMSLS_BCTR_I_UNDERFLOW Inverse transformation. “power” = #. The minimum element of “z” is “z[#]” = #. exp(“z[#]”) will underflow.
IMSLS_BCTR_I_OVERFLOW Inverse transformation. “power” = #. The maximum element of “z[#]” = #. exp(“z[#]”) will overflow.
IMSLS_BCTR_I_ABS_UNDERFLOW Inverse transformation. “power” = #. The element of “z” with the smallest absolute value is “z[#]” = #. “z[#]” ^ (1/ “power”) will underflow.
IMSLS_BCTR_I_ABS_OVERFLOW Inverse transformation. “power” = #. The element of “z” with the largest absolute value is “z[#]” = #. “z[#]” ^ (1/ “power”) will overflow.
