Evaluates the chi-squared cumulative distribution function (CDF).
Synopsis
#include <imsls.h>
float imsls_f_chi_squared_cdf (float chi_squared, float df)
The type double function is imsls_d_chi_squared_cdf.
Required Arguments
float
chi_squared (Input)
Argument for which the chi-squared
distribution function is to be evaluated.
float df
(Input)
Number of degrees of freedom of the chi-squared distribution.
Argument df must
be greater than 0.
Return Value
The probability p that a chi-squared random variable takes a value less than or equal to chi_squared.
Description
Function imsls_f_chi_squared_cdf
evaluates the distribution function,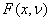 
, of a chi-squared random variable
x = chi_squared
with ν = df
degrees of freedom, where:
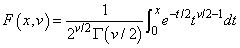
and Γ (⋅) is the gamma function. The value of the distribution function at the point x is the probability that the random variable takes a value less than or equal to x.
For v > vmax = 1.e7, imsls_f_chi_squared_cdf uses the Wilson-Hilferty approximation (Abramowitz and Stegun [A&S] 1964, Equation 26.4.17) for p in terms of the normal CDF, which is evaluated using function imsls_f_normal_cdf.
For v ≤ vmax, imsls_f_chi_squared_cdf uses series expansions to evaluate p: for x < ν, imsls_f_chi_squared_cdf calculates p using A&S series 6.5.29, and for x > ν, imsls_f_chi_squared_cdf calculates p using the continued fraction expansion of the incomplete gamma function given in A&S equation 6.5.31.
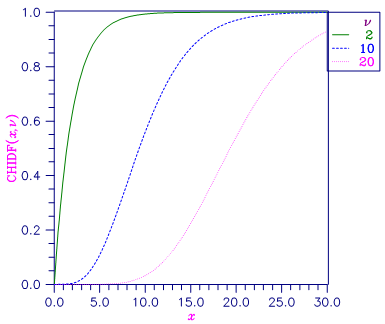
Figure 11-3 Plot of Fx (x, df)
Example
Suppose X is a chi-squared random variable with two degrees of freedom. In this example, we find the probability that X is less than 0.15 and the probability that X is greater than 3.0.
#include <imsls.h>
#include <stdio.h>
int main()
{
float chi_squared = 0.15, df = 2.0, p;
p = imsls_f_chi_squared_cdf(chi_squared, df);
printf("The probability that chi-squared"
" with %1.0f df is less than %4.2f is %5.4f\n",
df, chi_squared, p);
chi_squared = 3.0;
p = 1.0 - imsls_f_chi_squared_cdf(chi_squared, df);
printf("The probability that chi-squared"
" with %1.0f df is greater than %3.1f is %5.4f\n",
df, chi_squared, p);
}
Output
The probability that chi-squared with 2 df is less than 0.15 is 0.0723
The probability that chi-squared with 2 df is greater than 3.0 is 0.2231
Informational Errors
IMSLS_ARG_LESS_THAN_ZERO Since “chi_squared” = # is less than zero, the distribution function is zero at “chi_squared.”
Alert Errors
IMSLS_NORMAL_UNDERFLOW Using the normal distribution for large degrees of freedom, underflow would have occurred.
