Evaluates the complement of the Student’s t distribution.
Synopsis
#include <imsls.h>
float imsls_f_complementary_t_cdf (float t, float df)
The type double function is imsls_d_complementary_t_cdf.
Required Arguments
float t
(Input)
Argument for which Pr(x > t) is to be
evaluated.
float df
(Input)
Degrees of freedom. Argument df must be greater
than or equal to 1.0.
Return Value
The probability that a Student’s t random variable takes a value greater than t.
Description
Function imsls_f_complementary_t_cdf
evaluates one minus the distribution function of a Student’s t random
variable with 
= df
degrees of freedom. If 
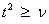, the following identity
relating the complementary Student’s t cumulative distribution
function, denoted by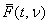 
, to the incomplete beta ratio
function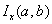 
is used:
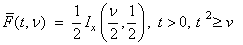
where
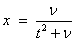
and
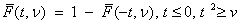
If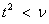 
, the solution space is partitioned
into four algorithms as follows: If > 64 and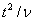 
< 0.1, a
Cornish-Fisher expansion is used to evaluate the distribution function. If
< 64 and an integer and
|t| < 2.0, a trigonometric series is used (see
Abramowitz and Stegun 1964, Equations 26.7.3 and 26.7.4 with some
rearrangement). If < 64 and an
integer and |t| > 2.0, a series given by Hill (1970)
that converges well for large values of t is used. For the
remaining 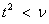cases, 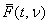is calculated using the
identity:
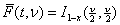
where
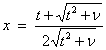
This function provides higher right tail accuracy for the Student's t distribution.
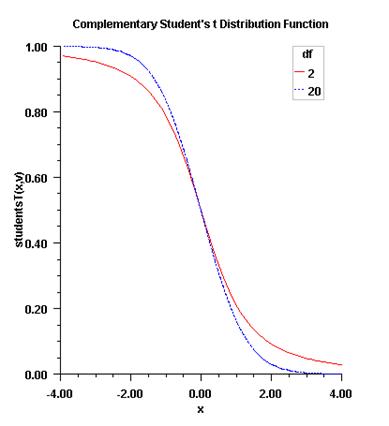
Figure 11-10 Plot of Ft (t, df)
Example
This example finds the 2-tail probability that a Student’s t random variable exceeds 2.447.
#include <imsls.h>
#include <stdio.h>
int main ()
{
float t = 2.447, df = 6.0, p;
p = 2.0*imsls_f_complementary_t_cdf(t,df);
printf("Pr(|t(%1.0f)| > %4.3f) = %6.4f\n", df, t, p);
}
Output
Pr(|t(6)| > 2.447) = 0.0500
