Performs a linear or a quadratic discriminant function analysis among several known groups.
Synopsis
#include <imsls.h>
void imsls_f_discriminant_analysis (int n_rows, int n_variables, float *x, int n_groups, ..., 0)
The type double function is imsls_d_discriminant_analysis.
Required Arguments
int n_rows
(Input)
Number of rows of x to be processed.
int
n_variables (Input)
Number of variables to be used in the
discrimination.
float *x
(Input)
Array of size n_rows by n_variables + 1
containing the data. The first n_variables columns
correspond to the variables, and the last column (column n_variables) contains
the group numbers. The groups must be numbered 1, 2, ..., n_groups.
int n_groups
(Input)
Number of groups in the data.
Synopsis with Optional Arguments
#include <imsls.h>
void
imsls_f_discriminant_analysis
(int n_rows,
int n_variables,
float *x,
int n_groups,
IMSLS_X_COL_DIM, int
x_col_dim,
IMSLS_X_INDICES, int
igrp, int
ind[], int
ifrq, int
iwt,
IMSLS_METHOD, int
method,
IMSLS_IDO, int
ido,
IMSLS_ROWS_ADD,
IMSLS_ROWS_DELETE,
IMSLS_PRIOR_EQUAL,
IMSLS_PRIOR_PROPORTIONAL,
IMSLS_PRIOR_INPUT, float
prior_input[],
IMSLS_PRIOR_OUTPUT, float
**prior_output
IMSLS_PRIOR_OUTPUT_USER, float
prior_output[]
IMSLS_GROUP_COUNTS, int
**gcounts,
IMSLS_GROUP_COUNTS_USER, int
gcounts[]
IMSLS_MEANS, float
**means,
IMSLS_MEANS_USER, float
means[],
IMSLS_COV, float
**covariances,
IMSLS_COV_USER,
float
covariances[],
IMSLS_COEF, float
**coefficients
IMSLS_COEF_USER, float
coefficients[],
IMSLS_CLASS_MEMBERSHIP, int
**class_membership,
IMSLS_CLASS_MEMBERSHIP_USER, int
class_membership[],
IMSLS_CLASS_TABLE, float
**class_table,
IMSLS_CLASS_TABLE_USER, float
class_table[],
IMSLS_PROB, float
**prob,
IMSLS_PROB_USER, float
prob[],
IMSLS_MAHALANOBIS, float
**d2,
IMSLS_MAHALANOBIS_USER,
float
d2[],
IMSLS_STATS, float
**stats,
IMSLS_STATS_USER, float
stats[],
IMSLS_N_ROWS_MISSING, int
*nrmiss,
0)
Optional Arguments
IMSLS_X_COL_DIM, int x_col_dim
(Input)
Column dimension of array x.
Default: x_col_dim = n_variables + 1
IMSLS_X_INDICES, int igrp, int ind[], int ifrq, int iwt
(Input)
Each of the four arguments contains indices indicating column numbers
of x in which
particular types of data are stored. Columns are numbered 0 … x_col_dim − 1.
Parameter igrp contains the index for the column of x in which the group numbers are stored.
Parameter ind contains the indices of the variables to be used in the analysis.
Parameters ifrq and iwt contain the column numbers of x in which the frequencies and weights, respectively, are stored. Set ifrq = −1 if there will be no column for frequencies. Set iwt = −1 if there will be no column for weights. Weights are rounded to the nearest integer. Negative weights are not allowed.
Defaults: igrp = n_variables, ind[] = 0, 1, ..., n_variables − 1, ifrq = −1, and iwt = −1
IMSLS_METHOD, int method
(Input)
Method of discrimination. The method chosen determines whether linear
or quadratic discrimination is used, whether the group covariance matrices are
computed (the pooled covariance matrix is always computed), and whether the
leaving-out-one or the reclassification method is used to classify each
observation.
|
method |
discrimination method |
covariances computed |
classification method |
|
1 |
linear |
pooled, group |
reclassification |
|
2 |
quadratic |
pooled, group |
reclassification |
|
3 |
linear |
pooled |
reclassification |
|
4 |
linear |
pooled, group |
leaving-out-one |
|
5 |
quadratic |
pooled, group |
leaving-out-one |
|
6 |
linear |
pooled |
leaving-out-one |
In the leaving-out-one method of classification, the posterior probabilities are adjusted so as to eliminate the effect of the observation from the sample statistics prior to its classification. In the classification method, the effect of the observation is not eliminated from the classification function.
When optional argument IMSLS_IDO is specified, the following rules for mixing methods apply; Methods 1, 2, 4, and 5 can be intermixed, as can methods 3 and 6. Methods 1, 2, 4, and 5 cannot be intermixed with methods 3 and 6.
Default: method = 1
IMSLS_IDO, int ido
(Input)
Processing option. See Comments 3 and 4 for more information.
|
ido |
Action |
|
0 |
This is the only invocation; all the data are input at once. (Default) |
|
1 |
This is the first invocation with this data; additional calls will be made. Initialization and updating for the n_rows observations of x will be performed. |
|
2 |
This is an intermediate invocation; updating for the n_rows observations of x will be performed. |
|
3 |
All statistics are updated for the n_rows observations. The discriminant functions and other statistics are computed. |
|
4 |
The discriminant functions are used to classify each of the n_rows observations of x. |
|
5 |
The covariance matrices are computed, and workspace is released. No further call to discriminant_analysis with ido greater than 1 should be made without first calling discriminant_analysis with ido = 1. |
|
6 |
Workspace is released. No further calls to discriminant_analysis with ido greater than 1 should be made without first calling discriminant_analysis with ido = 1. Invocation with this option is not required if a call has already been made with ido = 5. |
Default: ido = 0
IMSLS_ROWS_ADD, or
IMSLS_ROWS_DELETE
(Input)
By default (or if IMSLS_ROWS_ADD is
specified), then the observations in x are added to the
discriminant statistics. If IMSLS_ROWS_DELETE is
specified, then the observations are deleted.
If ido = 0, these optional arguments are ignored (data is always added if there is only one invocation).
IMSLS_PRIOR_EQUAL, or
IMSLS_PRIOR_PROPORTIONAL, or
IMSLS_PRIOR_INPUT, float
prior_input[] (Input)
By default, (or if IMSLS_PRIOR_EQUAL is
specified), equal prior probabilities are calculated as 1.0/n_groups.
If IMSLS_PRIOR_PROPORTIONAL is specified, prior probabilities are calculated to be proportional to the sample size in each group.
If IMSLS_PRIOR_INPUT is specified, then array prior_input is an array of length n_groups containing the prior probabilities for each group, such that the sum of all prior probabilities is equal to 1.0. Prior probabilities are not used if ido is equal to 1, 2, 5, or 6.
IMSLS_PRIOR_OUTPUT, float
**prior_output (Output)
Address of a pointer to an array
of length n_groups containing
the most recently calculated or input prior probabilities. If IMSLS_PRIOR_PROPORTIONAL
is specified, every element of prior_output is equal
to −1 until
a call is made with ido equal to 0 or 3,
at which point the priors are calculated. Note that subsequent calls to discriminant_analysis
with IMSLS_PRIOR_PROPORTIONAL
specified, and ido not equal to 0 or 3 will result in the elements of prior_output being
reset to −1.
IMSLS_PRIOR_OUTPUT_USER, float
prior_output[] (Output)
Storage for array prior_output is
provided by the user. See IMSLS_PRIOR_OUTPUT.
IMSLS_GROUP_COUNTS, int **gcounts
(Output)
Address of a pointer to an integer array of length n_groups containing
the number of observations in each group. Array gcounts is updated when ido is
equal to 0, 1, or 2.
IMSLS_GROUP_COUNTS_USER, int gcounts[]
(Output)
Storage for integer array gcounts is provided by
the user. See IMSLS_GROUP_COUNTS.
IMSLS_MEANS, float **means
(Output)
Address of a pointer to an array of size n_groups by n_variables. The
i-th row of means contains the group i variable means. Array means
is updated when ido is equal to 0, 1,
2, or 5. The means are unscaled until a call is made with ido = 5.
where the unscaled means are calculated as Σwifi xi and the scaled
means as
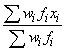
where xi is the value of the i-th observation, wi is the weight of the i-th observation, and fi is the frequency of the i-th observation.
IMSLS_MEANS_USER, float means[]
(Output)
Storage for array means is
provided by the user. See IMSLS_MEANS.
IMSLS_COV, float
**covariances (Output)
Address of a pointer to an array of
size g by n variables by n_variables
containing the within-group covariance matrices (methods 1, 2, 4, and 5
only) as the first g-1 matrices, and the pooled covariance matrix as the
g-th matrix (that is, the first n_variables ∗ n_variables elements
comprise the group 1 covariance matrix, the next n_variables ∗ n_variables elements
comprise the group 2 covariance, ..., and the last n_variables ∗ n_variables elements
comprise the pooled covariance matrix). If method is 3 or 6 then
g is equal to 1. Otherwise, g is equal to n_groups + 1. Argument
cov is updated
when ido is
equal to 0, 1, 2, 3, or 5.
IMSLS_COV_USER, float
covariances[] (Output)
Storage for array covariances is
provided by the user. See IMSLS_COVARIANCES.
IMSLS_COEF, float
**coefficients (Output)
Address of a pointer to an array
of size n_groups
by
(n_variables + 1)
containing the linear discriminant coefficients. The first column of coefficients contains
the constant term, and the remaining columns contain the variable coefficients.
Row i − 1 of coefficients
corresponds to group i, for
i = 1, 2, ..., n_variables + 1. Array coefficients are
always computed as the linear discriminant function coefficients even when
quadratic discrimination is specified.
Array coefficients is updated when ido is equal to 0 or 3.
IMSLS_COEF_USER, float
coefficients[] (Output)
Storage for array coefficients is
provided by the user. See IMSLS_COEFFICIENTS.
IMSLS_CLASS_MEMBERSHIP, int
**class_membership (Output)
Address of a pointer to an
integer array of length n_rows containing the
group to which the observation was classified. Array class_membership is
updated when ido
is equal to 0 or 4.
If an observation has an invalid group number, frequency, or weight when the leaving-out-one method has been specified, then the observation is not classified and the corresponding elements of class_membership (and prob, see IMSLS_PROB) are set to zero.
IMSLS_CLASS_MEMBERSHIP_USER, int
class_membership[] (Ouput)
Storage for array class_membership is
provided by the user. See IMSLS_CLASS_MEMBERSHIP.
IMSLS_CLASS_TABLE, float
**class_table (Output)
Address of a pointer to an array of
size n_groups by
n_groups
containing the classification table. Array class_table is updated
when ido is
equal to 0, 1, or 4. Each observation that is classified and has a group number
1.0, 2.0, ..., n_groups is entered
into the table. The rows of the table correspond to the known group membership.
The columns refer to the group to which the observation was classified.
Classification results accumulate with each call to imsls_f_discriminant_analysis
with ido equal
to 4. For example, if two calls with ido equal to 4 are
made, the elements in class_table sum to the
total number of valid observations in the two calls.
IMSLS_CLASS_TABLE_USER, float
class_table[] (Output)
Storage for array class_table is
provided by the user. See IMSLS_CLASS_TABLE.
IMSLS_PROB, float **prob
(Output)
Address of a pointer to an array of size n_rows by n_groups containing
the posterior probabilities for each observation. Argument prob is updated when
ido is equal to
0 or 4.
IMSLS_PROB_USER, float prob[]
(Output)
Storage for array prob is provided by
the user. See IMSLS_PROB.
IMSLS_MAHALANOBIS, float **d2
(Output)
Address of a pointer to an array of size n_groups by n_groups containing
the Mahalanobis distances
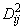
between the group means. Argument d2 is updated when ido is equal to 0 or 3.
For linear discrimination, the Mahalanobis distance is computed using the pooled covariance matrix. Otherwise, the Mahalanobis distance
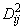
between group means i and j is computed using the within covariance matrix for group i in place of the pooled covariance matrix.
IMSLS_MAHALANOBIS_USER, float d2[]
(Output)
Storage for array d2 is provided by the
user. See IMSLS_MAHALANOBIS.
IMSLS_STATS, float **stats
(Output)
Address of a pointer to an array of length 4 + 2 × (n_groups + 1)
containing various statistics of interest. Array stats is updated when
ido is equal to
0, 2, 3, or 5. The first element of stats is the sum of
the degrees of freedom for the within-covariance matrices. The second,
third, and fourth elements of stats correspond to
the chi-squared statistic, its degrees of freedom, and the probability of a
greater
chi-squared, respectively, of a test of the homogeneity of the
within-covariance matrices (not computed if method is equal to 3
or 6). The fifth through 5 + n_groups elements of
stats contain
the log of the determinants of each group’s covariance matrix (not computed if
method is equal
to 3 or 6) and of the pooled covariance matrix (element 4 + n_groups). Finally,
the last n_groups + 1
elements of stats contain the sum
of the weights within each group, and in the last position, the sum of the
weights in all groups.
IMSLS_STATS_USER, float stats[]
(Output)
Storage for array stats is provided by
the user. See IMSLS_STATS_USER.
IMSLS_N_ROWS_MISSING, int *nrmiss
(Output)
Number of rows of data encountered in calls to discriminant_analysis
containing missing values (NaN) for the classification, group, weight, and/or
frequency variables. If a row of data contains a missing value (NaN) for any of
these variables, that row is excluded from the computations.
Array nrmiss is updated when ido is equal to 0, 1, 2, or 3.
Comments
1. Common
choices for the Bayesian prior probabilities are given by:
prior_input[i] = 1.0∕n_groups
(equal priors)
prior_input[i] = gcounts∕n_rows
(proportional priors)
prior_input[i] = Past
history or subjective judgment.
In all cases, the priors should sum to
1.0.
2. Two passes of the data are made. In the first pass, the statistics required to compute the discriminant functions are obtained (ido equal to 1, 2, and 3). In the second pass, the discriminant functions are used to classify the observations. When ido is equal to 0, all of the data are memory resident, and both passes are made in one call to imsls_f_discriminant_analysis. When ido > 0 (optional argument IMSLS_IDO is specified), a third call to imsls_f_discriminant_analysis involving no data is required with ido equal to 5 or 6.
3. Here are a few rules and guidelines for the correct value of ido in a series of calls:
1 Calls with ido = 0 or ido = 1 may be made at any time, subject to rule 2. These calls indicate that a new analysis is to begin, and therefore allocate memory and destroy all statistics from previous calls.
2 Each series of calls to imsls_f_discriminant_analysis which begins with ido = 1 must end with ido equal to 5 or 6 to ensure the proper release of workspace, subject to rule 3.
3 ido may not be 4 or 5 before a call with ido = 3 has been made.
4
ido may not be
2, 3, 4, 5, or 6
a) Immediately after a call with ido = 0.
b)
Before a call with ido = 1 has
been made.
c) Immediately after a call with ido equal to 5 or 6
has been made.
The following is a valid sequence of ido’s:
|
ido |
Explanation |
|
0 |
Data Set A: Perform a complete analysis. All data to be used in the analysis must be present in x. Since cleanup of workspace is automatic for ido = 0, no further calls are necessary. |
|
1 |
Data Set B: Begin analysis. The n_rows observations in x are used for initialization. |
|
2 |
Data Set B: Continue analysis. New observations placed in x are added to (or deleted from, see IMSLS_ROWS_DELETE) the analysis. |
|
2 |
Data Set B: Continue analysis. n_rows new observations placed in x are added to (or deleted from, see IMSLS_ROWS_DELETE) the analysis. |
|
3 |
Data Set B: Continue analysis. n_rows new observations are added (or deleted) and discriminant functions and other statistics are computed. |
|
4 |
Data Set B: Classification of each of the n_rows observations in the current x matrix. |
|
5 |
Data Set B: End analysis. Covariance matrices are computed and workspace is released. This analysis could also have been ended by choosing ido = 6 |
|
1 |
Data Set C: Begin analysis. Note that for this call to be valid the previous call must have been made with ido equal to 5 or 6. |
|
3 |
Data Set C: Continue analysis. |
|
4 |
Data Set C: Continue analysis. |
|
3 |
Data Set C: Continue analysis. |
|
6 |
Data Set C: End analysis. |
4. Because of the internal workspace allocation and saved variables, function imsls_f_discriminant_analysis must complete the analysis of a data set before beginning processing of the next data set.
Description
Function imsls_f_discriminant_analysis performs discriminant function analysis using either linear or quadratic discrimination. The output includes a measure of distance between the groups, a table summarizing the classification results, a matrix containing the posterior probabilities of group membership for each observation, and the within-sample means and covariance matrices. The linear discriminant function coefficients are also computed.
By default (or if optional argument IMSLS_IDO is specified with ido = 0) all observations are input during one call, a method of operation that has the advantage of simplicity. Alternatively, one or more rows of observations can be input during separate calls. This method does not require that all observations be memory resident, a significant advantage with large data sets. Note, however, that the algorithm requires two passes of the data. During the first pass the discriminant functions are computed while in the second pass, the observations are classified. Thus, with the second method of operation, the data will usually need to be input twice.
Because both methods result in the same operations being performed, the algorithm is discussed as if only a few observations are input during each call. The operations performed during each call depend upon the ido parameter.
The ido = 1 step is the initialization step. “Private” internally allocated saved variables corresponding to means, class_table, and covariances are initialized to zero, and other program parameters are set (copies of these private variables are written to the corresponding output variables upon return from the function call, assuming ido values such that the results are to be returned). Parameters n_rows, x, and method can be changed from one call to the next within the two sets {1, 2, 4, 5} and {3, 6} but not between these sets when ido > 1. That is, do not specify method = 1 in one call and method = 3 in another call without first making a call with ido = 1.
After initialization has been performed in the ido = 1 step, the within-group means are updated for all valid observations in x. Observations with invalid group numbers are ignored, as are observation with missing values. The LU factorization of the covariance matrices are updated by adding (or deleting) observations via Givens rotations.
The ido = 2 step is used solely for adding or deleting observations from the model as in the above paragraph.
The ido = 3 step begins by adding all observations in x to the means and the factorizations of the covariance matrices. It continues by computing some statistics of interest: the linear discriminant functions, the prior probabilities (by default, or if IMSLS_PROPORTIONAL_PRIORS is specified), the log of the determinant of each of the covariance matrices, a test statistic for testing that all of the within-group covariance matrices are equal, and a matrix of Mahalanobis distances between the groups. The matrix of Mahalanobis distances is computed via the pooled covariance matrix when linear discrimination is specified; the row covariance matrix is used when the discrimination is quadratic.
Covariance matrices are defined as follows: Let Ni denote the sum of the frequencies of the observations in group i and Mi denote the number of observations in group i. Then, if Si denotes the within-group i covariance matrix,
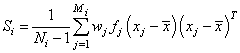
Where wj is the weight of the
j-th observation in group i, fj is the frequency,
xj is the j-th
observation column vector (in group i), and 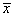 denotes the mean vector of the
observations in group i. The mean vectors are computed as
denotes the mean vector of the
observations in group i. The mean vectors are computed as
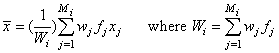
Given the means and the covariance matrices, the linear discriminant function for group i is computed as:
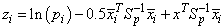
where ln (pi) is the natural log of the prior probability for the i-th group, x is the observation to be classified, and Sp denoted the pooled covariance matrix.
Let S denote either the pooled covariance matrix of one of the within-group covariance matrices Si. (S will be the pooled covariance matrix in linear discrimination, and Si otherwise.) The Mahalanobis distance between group i and group j is computed as:
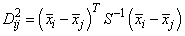
Finally, the asymptotic chi-squared test for the equality of covariance matrices is computed as follows (Morrison 1976, p. 252):
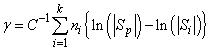
where ni is the number of degrees of freedom in the i-th sample covariance matrix, k is the number of groups, and
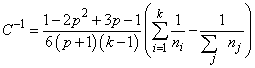
where p is the number of variables.
When ido = 4, the estimated posterior probability of each observation x belonging to group is computed using the prior probabilities and the sample mean vectors and estimated covariance matrices under a multivariate normal assumption. Under quadratic discrimination, the within-group covariance matrices are used to compute the estimated posterior probabilities. The estimated posterior probability of an observation x belonging to group i is
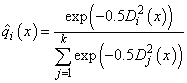
where
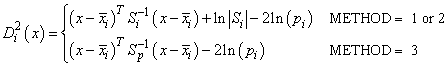
For the leaving-out-one method of classification (method equal to 4, 5 or 6), the sample mean vector and sample covariance matrices in the formula for
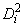
are adjusted so as to remove the observation x from their computation. For linear discrimination (method equal to 1, 3, 4, or 6), the linear discriminant function coefficients are actually used to compute the same posterior probabilities.
Using the posterior probabilities, each observation in x is classified into a group; the result is tabulated in the matrix class_table and saved in the vector class_membership. Matrix class_table is not altered at this stage if x[i][x_group] (by default, x_igrp = 0; see optional argument IMSLS_INDICES) contains a group number that is out of range. If the reclassification method is specified, then all observations with no missing values in the n_variables classification variables are classified. When the leaving-out-one method is used, observations with invalid group numbers, weights, frequencies, or classification variables are not classified. Regardless of the frequency, a 1 is added (or subtracted) from class_table for each row of x that is classified and contains a valid group number.
When method > 3, adjustment is made to the posterior probabilities to remove the effect of the observation in the classification rule. In this adjustment, each observation is presumed to have a weight of x[i][iwt] if iwt > −1 (and a weight of 1.0 if iwt = −1), and a frequency of 1.0. See Lachenbruch (1975, p. 36) for the required adjustment.
Finally, when ido = 5, the covariance matrices are computed from their LU factorizations. Internally allocated and saved variables are cleaned up at this step (ido equal to 5 or 6).
Examples
Example 1
The following example uses liner discrimination with equal prior probabilities on Fisher’s (1936) Iris data. This example illustrates the execution of imsls_f_discriminant_analysis when one call is made (i.e. using the default of ido = 0).
#include <stdio.h>
#include <stdlib.h>
#include <imsls.h>
int main() {
int n_groups = 3;
int nrow, nvar, ncol, nrmiss;
float *x, *xtemp;
float *prior_out, *means, *cov, *coef;
float *table, *d2, *stats, *prob;
int *counts, *cm;
static int perm[5] = {1, 2, 3, 4, 0};
/* Retrieve the Fisher Iris Data Set
*/
xtemp = imsls_f_data_sets(3, IMSLS_N_OBSERVATIONS, &nrow,
IMSLS_N_VARIABLES, &ncol, 0);
nvar = ncol - 1;
/* Move the group column to end of the
the matrix */
x = imsls_f_permute_matrix(nrow, ncol, xtemp, perm,
IMSLS_PERMUTE_COLUMNS, 0);
imsls_free(xtemp);
imsls_f_discriminant_analysis (nrow,
nvar, x, n_groups,
IMSLS_METHOD, 3,
IMSLS_GROUP_COUNTS, &counts,
IMSLS_COEF, &coef,
IMSLS_MEANS, &means,
IMSLS_STATS, &stats,
IMSLS_CLASS_MEMBERSHIP, &cm,
IMSLS_CLASS_TABLE, &table,
IMSLS_PROB, &prob,
IMSLS_MAHALANOBIS, &d2,
IMSLS_COV, &cov,
IMSLS_PRIOR_OUTPUT, &prior_out,
IMSLS_N_ROWS_MISSING, &nrmiss,
IMSLS_PRIOR_EQUAL,
IMSLS_METHOD, 3, 0);
imsls_i_write_matrix("Counts", 1,
n_groups, counts, 0);
imsls_f_write_matrix("Coef", n_groups, nvar+1, coef, 0);
imsls_f_write_matrix("Means", n_groups, nvar, means, 0);
imsls_f_write_matrix("Stats", 12, 1, stats, 0);
imsls_i_write_matrix("Membership", 1, nrow, cm, 0);
imsls_f_write_matrix("Table", n_groups, n_groups, table, 0);
imsls_f_write_matrix("Prob", nrow, n_groups, prob, 0);
imsls_f_write_matrix("D2", n_groups, n_groups, d2, 0);
imsls_f_write_matrix("Covariance", nvar, nvar, cov, 0);
imsls_f_write_matrix("Prior OUT", 1, n_groups, prior_out, 0);
printf("\nnrmiss = %3d\n", nrmiss);
imsls_free(means);
imsls_free(stats);
imsls_free(counts);
imsls_free(coef);
imsls_free(cm);
imsls_free(table);
imsls_free(prob);
imsls_free(d2);
imsls_free(prior_out);
imsls_free(cov);
}
Output
Counts
1 2 3
50 50 50
Coef
1 2 3 4 5
1 -86.3 23.5 23.6 -16.4 -17.4
2 -72.9 15.7 7.1 5.2 6.4
3 -104.4 12.4 3.7 12.8 21.1
Means
1 2 3 4
1 5.006 3.428 1.462 0.246
2 5.936 2.770 4.260 1.326
3 6.588 2.974 5.552 2.026
Stats
1 147
2 ..........
3 ..........
4 ..........
5 ..........
6 ..........
7 ..........
8 -10
9 50
10 50
11 50
12 150
Membership
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115
2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147
3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3
148 149 150
3 3 3
Table
1 2 3
1 50 0 0
2 0 48 2
3 0 1 49
Prob
1 2 3
1 1.000 0.000 0.000
2 1.000 0.000 0.000
3 1.000 0.000 0.000
4 1.000 0.000 0.000
5 1.000 0.000 0.000
6 1.000 0.000 0.000
7 1.000 0.000 0.000
8 1.000 0.000 0.000
9 1.000 0.000 0.000
10 1.000 0.000 0.000
11 1.000 0.000 0.000
12 1.000 0.000 0.000
13 1.000 0.000 0.000
14 1.000 0.000 0.000
15 1.000 0.000 0.000
16 1.000 0.000 0.000
17 1.000 0.000 0.000
18 1.000 0.000 0.000
19 1.000 0.000 0.000
20 1.000 0.000 0.000
21 1.000 0.000 0.000
22 1.000 0.000 0.000
23 1.000 0.000 0.000
24 1.000 0.000 0.000
25 1.000 0.000 0.000
26 1.000 0.000 0.000
27 1.000 0.000 0.000
28 1.000 0.000 0.000
29 1.000 0.000 0.000
30 1.000 0.000 0.000
31 1.000 0.000 0.000
32 1.000 0.000 0.000
33 1.000 0.000 0.000
34 1.000 0.000 0.000
35 1.000 0.000 0.000
36 1.000 0.000 0.000
37 1.000 0.000 0.000
38 1.000 0.000 0.000
39 1.000 0.000 0.000
40 1.000 0.000 0.000
41 1.000 0.000 0.000
42 1.000 0.000 0.000
43 1.000 0.000 0.000
44 1.000 0.000 0.000
45 1.000 0.000 0.000
46 1.000 0.000 0.000
47 1.000 0.000 0.000
48 1.000 0.000 0.000
49 1.000 0.000 0.000
50 1.000 0.000 0.000
51 0.000 1.000 0.000
52 0.000 0.999 0.001
53 0.000 0.996 0.004
54 0.000 1.000 0.000
55 0.000 0.996 0.004
56 0.000 0.999 0.001
57 0.000 0.986 0.014
58 0.000 1.000 0.000
59 0.000 1.000 0.000
60 0.000 1.000 0.000
61 0.000 1.000 0.000
62 0.000 0.999 0.001
63 0.000 1.000 0.000
64 0.000 0.994 0.006
65 0.000 1.000 0.000
66 0.000 1.000 0.000
67 0.000 0.981 0.019
68 0.000 1.000 0.000
69 0.000 0.960 0.040
70 0.000 1.000 0.000
71 0.000 0.253 0.747
72 0.000 1.000 0.000
73 0.000 0.816 0.184
74 0.000 1.000 0.000
75 0.000 1.000 0.000
76 0.000 1.000 0.000
77 0.000 0.998 0.002
78 0.000 0.689 0.311
79 0.000 0.993 0.007
80 0.000 1.000 0.000
81 0.000 1.000 0.000
82 0.000 1.000 0.000
83 0.000 1.000 0.000
84 0.000 0.143 0.857
85 0.000 0.964 0.036
86 0.000 0.994 0.006
87 0.000 0.998 0.002
88 0.000 0.999 0.001
89 0.000 1.000 0.000
90 0.000 1.000 0.000
91 0.000 0.999 0.001
92 0.000 0.998 0.002
93 0.000 1.000 0.000
94 0.000 1.000 0.000
95 0.000 1.000 0.000
96 0.000 1.000 0.000
97 0.000 1.000 0.000
98 0.000 1.000 0.000
99 0.000 1.000 0.000
100 0.000 1.000 0.000
101 0.000 0.000 1.000
102 0.000 0.001 0.999
103 0.000 0.000 1.000
104 0.000 0.001 0.999
105 0.000 0.000 1.000
106 0.000 0.000 1.000
107 0.000 0.049 0.951
108 0.000 0.000 1.000
109 0.000 0.000 1.000
110 0.000 0.000 1.000
111 0.000 0.013 0.987
112 0.000 0.002 0.998
113 0.000 0.000 1.000
114 0.000 0.000 1.000
115 0.000 0.000 1.000
116 0.000 0.000 1.000
117 0.000 0.006 0.994
118 0.000 0.000 1.000
119 0.000 0.000 1.000
120 0.000 0.221 0.779
121 0.000 0.000 1.000
122 0.000 0.001 0.999
123 0.000 0.000 1.000
124 0.000 0.097 0.903
125 0.000 0.000 1.000
126 0.000 0.003 0.997
127 0.000 0.188 0.812
128 0.000 0.134 0.866
129 0.000 0.000 1.000
130 0.000 0.104 0.896
131 0.000 0.000 1.000
132 0.000 0.001 0.999
133 0.000 0.000 1.000
134 0.000 0.729 0.271
135 0.000 0.066 0.934
136 0.000 0.000 1.000
137 0.000 0.000 1.000
138 0.000 0.006 0.994
139 0.000 0.193 0.807
140 0.000 0.001 0.999
141 0.000 0.000 1.000
142 0.000 0.000 1.000
143 0.000 0.001 0.999
144 0.000 0.000 1.000
145 0.000 0.000 1.000
146 0.000 0.000 1.000
147 0.000 0.006 0.994
148 0.000 0.003 0.997
149 0.000 0.000 1.000
150 0.000 0.018 0.982
D2
1 2 3
1 0.0 89.9 179.4
2 89.9 0.0 17.2
3 179.4 17.2 0.0
Covariance
1 2 3 4
1 0.2650 0.0927 0.1675 0.0384
2 0.0927 0.1154 0.0552 0.0327
3 0.1675 0.0552 0.1852 0.0427
4 0.0384 0.0327 0.0427 0.0419
Prior OUT
1 2 3
0.3333 0.3333 0.3333
nrmiss = 0
Example 2
Continuing with Fisher’s Iris data, the example below computes the quadratic discriminant functions using values of IDO greater than 0. In the first loop, all observations are added to the functions, one at a time. In the second loop, each of the observations is classified, one by one, using the leaving-out-one method.
#include <stdio.h>
#include <stdlib.h>
#include <imsls.h>
int main() {
int n_groups = 3;
int nrow, nvar, ncol, i, nrmiss;
float *x, *xtemp;
float *prior_out, *means, *cov, *coef;
float *table, *d2, *stats, *prob;
int *counts, *cm;
static int perm[5] = {1, 2, 3, 4, 0};
/* Retrieve the Fisher Iris Data Set
*/
xtemp = imsls_f_data_sets(3, IMSLS_N_OBSERVATIONS, &nrow,
IMSLS_N_VARIABLES, &ncol, 0);
nvar = ncol - 1;
/* Move the group column to end of the
the matrix */
x = imsls_f_permute_matrix(nrow, ncol, xtemp, perm,
IMSLS_PERMUTE_COLUMNS, 0);
imsls_free(xtemp);
prior_out = (float *)
malloc(n_groups*sizeof(float));
counts = (int *) malloc(n_groups*sizeof(int));
means = (float *) malloc(n_groups*nvar*sizeof(float));
cov = (float *) malloc(nvar*nvar*(ngroups+1)*sizeof(float));
coef = (float *) malloc(n_groups*(nvar+1)*sizeof(float));
table = (float *) malloc(n_groups*n_groups*sizeof(float));
d2 = (float *) malloc(n_groups*n_groups*sizeof(float));
stats = (float *) malloc((4+2*(n_groups+1))*sizeof(float));
cm = (int *) malloc(nrow*sizeof(int));
prob = (float *) malloc(nrow*n_groups*sizeof(float));
/*Initialize Analysis*/
imsls_f_discriminant_analysis (0, nvar, x, n_groups,
IMSLS_IDO, 1,
IMSLS_METHOD, 2, 0);
/*Add In Each Observation*/
for (i=0;i<nrow;i=i+1) {
imsls_f_discriminant_analysis (1, nvar, (x+i*ncol), n_groups,
IMSLS_IDO, 2, 0);
}
/*Remove observation 0 from the
analysis */
imsls_f_discriminant_analysis (1, nvar, (x+0), n_groups,
IMSLS_ROWS_DELETE,
IMSLS_IDO, 2, 0);
/*Add observation 0 back into the
analysis */
imsls_f_discriminant_analysis (1, nvar, (x+0), n_groups,
IMSLS_IDO, 2, 0);
/*Compute statistics*/
imsls_f_discriminant_analysis (0, nvar, x, n_groups,
IMSLS_PRIOR_PROPORTIONAL,
IMSLS_PRIOR_OUTPUT_USER, prior_out,
IMSLS_IDO, 3, 0);
imsls_f_write_matrix("Prior OUT", 1,
n_groups, prior_out, 0);
/*Classify One observation at a time,
using proportional priors*/
for (i=0;i<nrow;i=i+1) {
imsls_f_discriminant_analysis (1, nvar, (x+i*ncol), n_groups,
IMSLS_IDO, 4,
IMSLS_CLASS_MEMBERSHIP_USER, (cm+i),
IMSLS_PROB_USER, (prob+i*n_groups), 0);
}
/*Compute covariance matrices and
release internal workspace*/
imsls_f_discriminant_analysis (0, nvar, x, n_groups,
IMSLS_IDO, 5,
IMSLS_COV_USER, cov,
IMSLS_GROUP_COUNTS_USER, counts,
IMSLS_COEF_USER, coef,
IMSLS_MEANS_USER, means,
IMSLS_STATS_USER, stats,
IMSLS_CLASS_TABLE_USER, table,
IMSLS_MAHALANOBIS_USER, d2,
IMSLS_N_ROWS_MISSING, &nrmiss, 0);
imsls_i_write_matrix("Counts", 1,
n_groups, counts, 0);
imsls_f_write_matrix("Coef", n_groups, nvar+1, coef, 0);
imsls_f_write_matrix("Means", n_groups, nvar, means, 0);
imsls_f_write_matrix("Stats", 12, 1, stats, 0);
imsls_i_write_matrix("Membership", 1, nrow, cm, 0);
imsls_f_write_matrix("Table", n_groups, n_groups, table, 0);
imsls_f_write_matrix("Prob", nrow, n_groups, prob, 0);
imsls_f_write_matrix("D2", n_groups, n_groups, d2, 0);
imsls_f_write_matrix("Covariance", nvar, nvar, cov, 0);
printf("\nnrmiss = %3d\n", nrmiss);
imsls_free(means);
imsls_free(stats);
imsls_free(counts);
imsls_free(coef);
imsls_free(cm);
imsls_free(table);
imsls_free(prob);
imsls_free(d2);
imsls_free(prior_out);
imsls_free(cov);
}
Output
Prior OUT
1 2 3
0.3333 0.3333 0.3333
Counts
1 2 3
50 50 50
Coef
1 2 3 4 5
1 -86.3 23.5 23.6 -16.4 -17.4
2 -72.9 15.7 7.1 5.2 6.4
3 -104.4 12.4 3.7 12.8 21.1
Means
1 2 3 4
1 5.006 3.428 1.462 0.246
2 5.936 2.770 4.260 1.326
3 6.588 2.974 5.552 2.026
Stats
1 147.0
2 143.8
3 20.0
4 0.0
5 -13.1
6 -10.9
7 -8.9
8 -10.0
9 50.0
10 50.0
11 50.0
12 150.0
Membership
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60
1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
2 2 2 2 2 2 2 2 2 2 3 2 2 2 2 2 2 2 2 2
81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99
2 2 2 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115
2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131
3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147
3 3 2 3 3 3 3 3 3 3 3 3 3 3 3 3
148 149 150
3 3 3
Table
1 2 3
1 50 0 0
2 0 48 2
3 0 1 49
Prob
1 2 3
1 1.000 0.000 0.000
2 1.000 0.000 0.000
3 1.000 0.000 0.000
4 1.000 0.000 0.000
5 1.000 0.000 0.000
6 1.000 0.000 0.000
7 1.000 0.000 0.000
8 1.000 0.000 0.000
9 1.000 0.000 0.000
10 1.000 0.000 0.000
11 1.000 0.000 0.000
12 1.000 0.000 0.000
13 1.000 0.000 0.000
14 1.000 0.000 0.000
15 1.000 0.000 0.000
16 1.000 0.000 0.000
17 1.000 0.000 0.000
18 1.000 0.000 0.000
19 1.000 0.000 0.000
20 1.000 0.000 0.000
21 1.000 0.000 0.000
22 1.000 0.000 0.000
23 1.000 0.000 0.000
24 1.000 0.000 0.000
25 1.000 0.000 0.000
26 1.000 0.000 0.000
27 1.000 0.000 0.000
28 1.000 0.000 0.000
29 1.000 0.000 0.000
30 1.000 0.000 0.000
31 1.000 0.000 0.000
32 1.000 0.000 0.000
33 1.000 0.000 0.000
34 1.000 0.000 0.000
35 1.000 0.000 0.000
36 1.000 0.000 0.000
37 1.000 0.000 0.000
38 1.000 0.000 0.000
39 1.000 0.000 0.000
40 1.000 0.000 0.000
41 1.000 0.000 0.000
42 1.000 0.000 0.000
43 1.000 0.000 0.000
44 1.000 0.000 0.000
45 1.000 0.000 0.000
46 1.000 0.000 0.000
47 1.000 0.000 0.000
48 1.000 0.000 0.000
49 1.000 0.000 0.000
50 1.000 0.000 0.000
51 0.000 1.000 0.000
52 0.000 1.000 0.000
53 0.000 0.998 0.002
54 0.000 0.997 0.003
55 0.000 0.997 0.003
56 0.000 0.989 0.011
57 0.000 0.995 0.005
58 0.000 1.000 0.000
59 0.000 1.000 0.000
60 0.000 0.994 0.006
61 0.000 1.000 0.000
62 0.000 0.999 0.001
63 0.000 1.000 0.000
64 0.000 0.988 0.012
65 0.000 1.000 0.000
66 0.000 1.000 0.000
67 0.000 0.973 0.027
68 0.000 1.000 0.000
69 0.000 0.813 0.187
70 0.000 1.000 0.000
71 0.000 0.336 0.664
72 0.000 1.000 0.000
73 0.000 0.699 0.301
74 0.000 0.972 0.028
75 0.000 1.000 0.000
76 0.000 1.000 0.000
77 0.000 0.998 0.002
78 0.000 0.861 0.139
79 0.000 0.992 0.008
80 0.000 1.000 0.000
81 0.000 1.000 0.000
82 0.000 1.000 0.000
83 0.000 1.000 0.000
84 0.000 0.154 0.846
85 0.000 0.943 0.057
86 0.000 0.996 0.004
87 0.000 0.999 0.001
88 0.000 0.999 0.001
89 0.000 1.000 0.000
90 0.000 0.999 0.001
91 0.000 0.981 0.019
92 0.000 0.997 0.003
93 0.000 1.000 0.000
94 0.000 1.000 0.000
95 0.000 0.999 0.001
96 0.000 1.000 0.000
97 0.000 1.000 0.000
98 0.000 1.000 0.000
99 0.000 1.000 0.000
100 0.000 1.000 0.000
101 0.000 0.000 1.000
102 0.000 0.000 1.000
103 0.000 0.000 1.000
104 0.000 0.006 0.994
105 0.000 0.000 1.000
106 0.000 0.000 1.000
107 0.000 0.004 0.996
108 0.000 0.000 1.000
109 0.000 0.000 1.000
110 0.000 0.000 1.000
111 0.000 0.006 0.994
112 0.000 0.001 0.999
113 0.000 0.000 1.000
114 0.000 0.000 1.000
115 0.000 0.000 1.000
116 0.000 0.000 1.000
117 0.000 0.033 0.967
118 0.000 0.000 1.000
119 0.000 0.000 1.000
120 0.000 0.041 0.959
121 0.000 0.000 1.000
122 0.000 0.000 1.000
123 0.000 0.000 1.000
124 0.000 0.028 0.972
125 0.000 0.001 0.999
126 0.000 0.007 0.993
127 0.000 0.057 0.943
128 0.000 0.151 0.849
129 0.000 0.000 1.000
130 0.000 0.020 0.980
131 0.000 0.000 1.000
132 0.000 0.009 0.991
133 0.000 0.000 1.000
134 0.000 0.605 0.395
135 0.000 0.000 1.000
136 0.000 0.000 1.000
137 0.000 0.000 1.000
138 0.000 0.050 0.950
139 0.000 0.141 0.859
140 0.000 0.000 1.000
141 0.000 0.000 1.000
142 0.000 0.000 1.000
143 0.000 0.000 1.000
144 0.000 0.000 1.000
145 0.000 0.000 1.000
146 0.000 0.000 1.000
147 0.000 0.000 1.000
148 0.000 0.001 0.999
149 0.000 0.000 1.000
150 0.000 0.061 0.939
D2
1 2 3
1 0.0 323.1 706.1
2 103.2 0.0 17.9
3 168.8 13.8 0.0
Covariance
1 2 3 4
1 0.1242 0.0992 0.0164 0.0103
2 0.0992 0.1437 0.0117 0.0093
3 0.0164 0.0117 0.0302 0.0061
4 0.0103 0.0093 0.0061 0.0111
nrmiss = 0
Warning Errors
IMSLS_BAD_OBS_1 In call #, row # of the data matrix, “x”, has group number = #. The group number must be an integer between 1.0 and “n_groups” = #, inclusively. This observation will be ignored.
IMSLS_BAD_OBS_2 The leaving out one method is specified but this observation does not have a valid group number (Its group number is #.). This observation (row #) is ignored.
IMSLS_BAD_OBS_3 The leaving out one method is specified but this observation does not have a valid weight or it does not have a valid frequency. This observation (row #) is ignored.
IMSLS_COV_SINGULAR_3 The group # covariance matrix is singular. “stats[1]” cannot be computed. “stats[1]” and “stats[3]” are set to the missing value code (NaN).
Fatal Errors
IMSLS_BAD_IDO_1 “ido” = #. Initial allocations must be performed by making a call to discriminant_analysis with “ido” = 1.
IMSLS_BAD_IDO_2 “ido” = #. A new analysis may not begin until the previous analysis is terminated with “ido” equal to 5 or 6.
IMSLS_COV_SINGULAR_1 The variance-covariance matrix for population number # is singular. The computations cannot continue.
IMSLS_COV_SINGULAR_2 The pooled variance-covariance matrix is singular. The computations cannot continue.
IMSLS_COV_SINGULAR_4 A variance-covariance matrix is singular. The index of the first zero element is equal to #.
