Optimizes a user defined fitness function using a tailored genetic algorithm.
Synopsis
#include <imsls.h>
Imsls_f_individual
*imsls_f_genetic_algorithm(float
fitness(),
Imsls_f_population
*initial_population,
...,
0)
The type double function is imsls_d_genetic_algorithm.
Required Arguments
float
fitness(Imsls_f_individual
*individual) (Input)
The fitness function. Given the
data structure for an individual within the population, fitness returns the
fitness of that individual. The fitness function must return non-negative
values.
Imsls_f_population *initial_population
(Input)
A pointer to the initial population.
Return Value
Function imsls_f_genetic_algorithm optimizes a user defined fitness function by evolving an initial population using a tailored genetic algorithm that searches for the fittest individual. It returns a pointer to a clone of the fittest individual in the last generation. Memory allocated to this data structure can be released using imsls_f_ga_free_individual.
Synopsis with Optional Arguments
#include <imsls.h>
Imsls_f_individual
*imsls_f_genetic_algorithm (float
fitness(),
Imsls_f_population *initial_population,
IMSLS_GRAY_ENCODING,
IMSLS_NO_ELITISM,
IMSLS_NO_DECODE,
IMSLS_PRINT_LEVEL,
int
level,
IMSLS_MAX_GENERATIONS, int
max_generations,
IMSLS_MAX_FITNESS,
float
max_fitness,
IMSLS_LINEAR_SCALING, float
c,
IMSLS_SIGMA_SCALING,
IMSLS_GENERATION_GAP,
float
p_gap,
IMSLS_MUTATION_PROB, float
p_mutation,
IMSLS_CROSSOVER_PROB, float
p_xover,
IMSLS_CROSSOVERS, int
n_xover,
IMSLS_PMX_CROSSOVER,
IMSLS_INVERT_CROSSOVER,
IMSLS_SELECTION_MODEL, int
selection_model,
IMSLS_FITNESS_FCN_WITH_PARMS,
float fitness(),
void
*parms,
IMSLS_N_GENERATIONS, int
*n_generations,
IMSLS_ON_LINE_PERFORMANCE,
float
**on_line_performance,
IMSLS_OFF_LINE_PERFORMANCE,
float
**off_line_performance,
IMSLS_VELOCITY,
float
**velocity,
IMSLS_GENERATION_STATS, float
**gen_statistics,
IMSLS_LAST_GENERATION,
Imsls_f_population **last_generation,
0)
Optional Arguments
IMSLS_GRAY_ENCODING
(Input)
By default, alleles for integer and real phenotypes are encoded
using Base-2 encoding. This argument changes that default to Gray encoding
for integer and real phenotypes.
IMSLS_NO_ELITISM
(Input)
By default, elitism is used to preserve the fittest individual
from one generation to the next. This argument disables elitism.
IMSLS_NO_DECODE
(Input)
By default, chromosome information is decoded into the
individual’s phenotypes before every call to the user’s fitness function.
This argument disables automatic decoding between generations. Decoding is only
applied to the last generation, including the fittest individual.
IMSLS_PRINT_LEVEL,
int level
(Input)
By default, no printing of intermediate and final results occur from
this function. The IMSLS_PRINT_LEVEL
argument accepts the following values for level:
|
level |
Enumeration |
Description |
|
0 |
IMSLS_NONE |
Supresses printing of any results. |
|
1 |
IMSLS_FINAL |
Prints summary of final results. |
|
2 |
IMSLS_TRACE_GEN |
Prints summary of final results plus generation statistics. |
|
3 |
IMSLS_TRACE_ALL |
Prints summary of final results, generation statistics and individual crossovers. |
IMSLS_MAX_GENERATIONS, int
max_generations (Input)
The maximum number of
generations. Optimization is halted when the number of generations exceeds
max_generations.
Default: max_generations=100.
IMSLS_MAX_FITNESS, float
max_fitness (Input)
The optimization is halted if the
maximum fitness is greater than this value.
Default: max_fitness=imsls_f_machine(7),
i.e., optimization is not halted by large fitness values. Optimization
only stops when the number of generations exceeds max_generations.
IMSLS_LINEAR_SCALING,
float
c (Input)
Specifies an upper limit for the linear fitness
scaling constant. Set c = 1 for no
scaling. A check is made to ensure that the minimum scaled fitness is
non-negative. If it falls below zero, then the scaling constant is
automatically reduced to make the minimum scaled fitness equal to zero.
For linear scaling the scaling constant is typically between one and two.
Default: c =1, no linear fitness
scaling.
IMSLS_SIGMA_SCALING
(Input)
By default, sigma scaling is not used for fitness
scaling. This argument enables sigma scaling.
IMSLS_GENERATION_GAP, float p_gap
(Input)
The proportion of weakest individuals replaced between
generations. If p_gap=1, all of the
individuals are replaced.
Default: p_gap=1.
IMSLS_MUTATION_PROB, float
p_mutation (Input)
The probability of mutation. Although
most applications set this to a value between 0.005 and 0.1, any value between 0
and 1 is allowed.
Default: p_mutation=0.005.
IMSLS_CROSSOVER_PROB, float p_xover
(Input)
The probability of crossover. p_xover can be any
value between 0 and 1. Most genetic algorithms use a probability between 0.6 and
0.9.
Default: p_xover= 0.6.
IMSLS_CROSSOVERS, int n_xover
(Input)
The number of crossover points. De Jong’s (1975) generalized crossover model R6 is
implemented. If n_xover is odd, then
the chromosome is treated as a string with a default crossover at the beginning
of the chromosome. If n_xover is even, then
the chromosome is treated as a ring with no beginning or end, and crossovers are
selected using the uniform distribution on a circle. Crossing points occur
at the odd crossover points. If the IMSLS_PMX_CROSSOVER
optional argument is used, there are always two crossover points within the
nominal portion of the chromosome. For partially matched crossovers, this
argument is only used to define the number of crossovers within the binary,
integer and real portion of the chromosome.
Default: n_xover=1.
IMSLS_PMX_CROSSOVER, (Input)
By default
this optional argument applies partially matched crossover to the nominal
portion of the chromosome. Crossovers for other phenotypes are still
applied using standard crossover and inversion crossover if requested.
With partially matched crossover, the number of crossovers for nominal
phenotypes is set to 2, and partially matched crossover is applied only to the
nominal phenotype. The number of crossovers for non-nominal phenotypes is
still controlled by the value of n_xover.
However, if this optional argument is used, crossover points are randomly
selected separately for nominal and non-nominal alleles.
IMSLS_INVERT_CROSSOVER, (Input)
This
option augments standard or partially matched crossover with inversion.
Inversion crossover inverts the values of the alleles in every other crossover
segment. If this is applied
with partially matched crossover, inversion is applied within the matched
segment of the alleles for the nominal phenotypes and then within every other
segment of any non-nominal phenotype.
IMSLS_SELECTION_MODEL, int
selection_model, (Input)
The model used for selecting
individuals for reproduction. Selection models are described in the
following table:
|
selection_model |
Description |
|
IMSLS_DETERMINISTIC |
Individuals with highest fitness are selected for reproduction using their expected sampling frequency. See Goldberg (1989) |
|
IMSLS_ROULETTE_WITH |
Original fitness-proportional selected described by Holland(1975). Sampling is done with replacement. |
|
IMSLS_ROULETTE_WITHOUT |
The original fitness-proportional selected except that sampling is done without replacement. This is also referred to as De Jong’s (1975) R3 model. |
|
IMSLS_REMAINDER_WITH |
Remainder selection with replacement. |
|
IMSLS_REMAINDER_WITH |
Remainder selection with replacement. |
|
IMSLS_REMAINDER_WITHOUT |
Remainder selection without replacement |
|
IMSLS_SUS_SELECTION |
Stochastic Universal Sampling as described by Baker (1987). |
|
IMSLS_RANK_SELECTION |
Rank selection. The individuals with the highest fitness are selected once for reproduction. |
|
IMSLS_TOURNAMENT_1 |
Tournament selection as described by Wetzel (1983). Only the fittest individual in a pair is selected. |
|
IMSLS_TOURNAMENT_2 |
Tournament selection as described by Goldberg and Deb (1991). The fittest individual in a pair is selected with probability 0.75. Otherwise the weaker individual is selected. |
Default: The original selection method described by Holland (1975), selection_model=IMSLS_ROULETTE_WITH.
IMSLS_FITNESS_FCN_WITH_PARMS, float
fitness(Imsls_f_individual *individual,
void
*parms), void *parms, (Input)
The fitness function calculated for
individual. If
this is supplied, fitness values are calculated for each individual and included
in the expanded population data structure. The parameters in parms are passed to
the function.
IMSLS_N_GENERATIONS, int
*n_generations (Output)
The number of generations used to
find the fittest individual.
IMSLS_ON_LINE_PERFORMANCE,
float **on_line_performance
(Output)
An array of length max_generations
containing on-line performance statistics for each generation.
IMSLS_OFF_LINE_PERFORMANCE,
float **off_line_performance
(Output)
An array of length max_generations
containing off-line performance statistics for each generation.
IMSLS_VELOCITY,
float **velocity
(Output)
An array of length max_generations
containing velocity statistics for each generation. The velocity for the
i-th generation is equal to 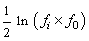 where
where 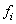 is the maximum fitness for the
i-th generation.
is the maximum fitness for the
i-th generation.
IMSLS_GENERATION_STATS,
float **gen_statistics
(Output)
An array of size max_generations*4
containing the maximum fitness, minimum fitness, average fitness and standard
deviation of the fitness for each generation. The
i-th row of
gen_statistics
contains the statistics for the i-th generation. When n_generations<max_generations,
rows greater than n_generations-1 are
filled with NaN values. The four columns contain the following statistics
calculated for each generation:
|
Column |
Description |
|
1 |
Maximum Fitness |
|
2 |
Minimum Fitness |
|
3 |
Fitness Average |
|
4 |
Fitness Standard Deviation |
IMSLS_LAST_GENERATION,
Imsls_f_population **last_generation
(Output)
The last generation produced by the genetic algorithm. Memory
allocated to this data structure can be released using imsls_f_ga_free_population.
Description
Genetic algorithms search for the optimum individual in a population. This is defined as the individual with the highest fitness. Function imsls_f_genetic_algorithm returns the fittest individual in the last generation. Mathematically, this is equivalent to finding the values of the phenotypes that maximize a user provided fitness function. Although there are no requirements that the fitness function be non-negative, in general, convergence to optimum fitness is faster when values of the fitness function are non-negative. Constraints can be applied by incorporating a penalty function within the fitness calculation. Phenotypes can consist of any combination of nominal, binary, integer and real values. Integer and real values must be encoded into a binary representation. This procedure provides for either Base-2 or Gray encoding. However, users can supply other encodings within the fitness function.
The function imsls_f_genetic_algorithm uses the population data structure and fitness with simulated genetic processes of reproduction to search for the optimum individual, i.e. settings of phenotype values. Genetic algorithms have been successfully applied to a wide variety of optimization and search problems, see Holland (1975) and Goldberg (1985).
There are many refinements to the basic genetic algorithm originally described by Holland (1975). His basic algorithm begins with an initial population of n individuals, a fitness function, and probabilities for crossover and mutation of p_xover and p_mutation respectively. The initial population is transformed from one generation to the next using the following steps:
1. Select n individuals from the current population to generate a mating pool.
2. Apply crossover with probability p_xover to pairs of the selected individuals within the mating pool to produce two offspring.
3. Apply mutation with probability p_mutation to the offspring to generate the next generation.
4. Check stopping criteria. If they are met, stop and report the fittest individual within the last generation.
By default Holland’s approach to these steps are used. However, many variations of these can be selected using optional arguments.
The initial population can be generated automatically using imsls_f_ga_random_population or it can be created by first creating individuals using imsls_f_ga_individual and then a population for those individuals using imsls_f_ga_population.
By default Holland’s roulette wheel with replacement is used for selecting the mating pool. The optional argument IMSLS_SELECTION_MODEL allows users to select alternate selection methods including remainder, tournament and stochastic universal selection. Default crossover and mutation probabilities are p_xover= 0.8 and p_mutation= 0.005. These defaults can be changed using the optional arguments IMSLS_CROSSOVER_PROB and IMSLS_MUTATION_PROB.
In the original algorithm only a single crossover point was randomly selected. The optional argument IMSLS_CROSSOVERS allows users to designate any number of crossover points.
Standard crossover proceeds by combining the genes from both parents in the order found in those parents. Inversion crossover inverts this order for one of the parents. Inversion crossover is selected using the optional argument IMSLS_INVERT_CROSSOVER.
For certain problems, such as the traveling salesman problem, standard crossover can produce infeasible individuals. One approach is to assign zero fitness to those solutions, but this can be very inefficient. Partially matched crossover is an approach that ensures individuals are feasible for a certain class of problems. If the problem is best represented using nominal phenotypes with values 0, 1, …, n_nominal-1 where all values must appear once and only once in the chromosome, then partially matched crossover preserves that condition. Partially matched crossover is selected using the optional argument IMSLS_PMX_CROSSOVER.
One issue with some applications of genetic algorithms is premature convergence or convergence to false local solutions. This can occur when dominant individuals within early generations take over the population prematurely reducing population diversity. One approach to this problem is fitness scaling. This implementation allows users to use either linear or sigma fitness scaling. By default, no scaling is used. However, the optional arguments IMSLS_LINEAR_SCALING and IMSLS_SIGMA_SCALING allow users to have fitness values automatically scaled before selection.
The genetic algorithm is stopped when any one of the stopping criteria is met. The algorithm is stopped when the number of generations exceeds max_generations or when the maximum fitness exceeds max_fitness. By default max_generations= 100; this can be changed using IMSLS_MAX_GENERATIONS. By default max_fitness is imsls_f_machine(7); this can be changed using IMSLS_MAX_FITNESS.
On some platforms, imsls_f_genetic_algorithm can evaluate the user-supplied function fitness in parallel. This is done only if the function imsls_omp_options is called to flag user-defined functions as thread-safe. A function is thread-safe if there are no dependencies between calls. Such dependencies are usually the result of writing to global or static variables.
Examples
Example 1
De Jong (1975) examined the performance of a genetic algorithm for finding the maximum of a multivariate function. This is an example of optimizing a variation of De Jong’s R2 function:
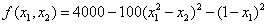
where
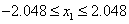 and
and
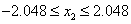 .
.
Since there were only two real phenotypes and the function is easily calculated, the phenotypes were encoded using discretization with 65,536 values over the interval [-2.048, 2.048]. By default, encoding and decoding is done within imsls_f_genetic_algorithm. This allows the fitness function to calculate individual fitness using the real phenotypes instead of the chromosome. Both the chromosome and its phenotype representation are available within the Imsls_f_individual data structure argument.
The default selection algorithm IMSLS_ROULETTE_WITH was used, but the number of crossover probability was set to 0.6. The genetic algorithm was more efficient using a lower crossover probability and Gray encoding instead of the defaults 0.7 and Base-2 encoding. Each generation consisted of 40 individuals.
#include <imsls.h>
#include <stdio.h>
int main(){
int i, j; /* index variables */
int n = 40; /* population size */
int n_generations = 0; /* final number of generations*/
int n_real = 2; /* number of real phenotypes */
int r_intervals[2] = {65536, 65536};
float r_bounds[4] = {-2.048, 2.048, -2.048, 2.048};
float* genStats; /* generation statistics */
static float deJongR2(Imsls_f_individual* individual);
Imsls_f_chromosome* chromosome; /* chromosome data structure */
Imsls_f_individual* best_individual;/* optimum */
Imsls_f_population* population; /* population data structure */
Imsls_f_population* last_generation;/* last generation */
char *dashes=
"**************************************************************";
/******************************************************************/
/* In this example the user function is thread safe. Let CNL */
/* know it is safe, which allows genetic algorithm to run in */
/* parallel, if that capability exists on the user computer. */
/******************************************************************/
imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
imsls_random_seed_set(12345);
chromosome = imsls_f_ga_chromosome(
IMSLS_REAL, n_real, r_intervals, r_bounds, 0);
population = imsls_f_ga_random_population(n, chromosome,
IMSLS_GRAY_ENCODING,
IMSLS_FITNESS_FCN, deJongR2, 0);
best_individual = imsls_f_genetic_algorithm(deJongR2, population,
IMSLS_PRINT_LEVEL, IMSLS_FINAL,
IMSLS_MAX_FITNESS, 3999.999,
IMSLS_CROSSOVER_PROB, 0.6,
IMSLS_GRAY_ENCODING,
IMSLS_MAX_GENERATIONS, 1000,
IMSLS_N_GENERATIONS, &n_generations,
IMSLS_GENERATION_STATS, &genStats,
IMSLS_LAST_GENERATION,&last_generation, 0);
printf(
"\n*****************GENERATION STATISTICS*****************\n");
printf("Generation Max. Fit. Avg. Fit. Min. Fit. CV\n");
printf("*******************************************************\n");
for(i=0; i<=n_generations; i++){
printf("Gen. %3d: %11.5f %10.2f %10.2f %9.2f \n",
i, genStats[4*i], genStats[4*i+2], genStats[4*i+1],
100*genStats[4*i+3]/genStats[4*i+2]);
}
printf("\nLAST GENERATION\n");
printf("%s\n",dashes);
printf("\nIndv Fitness ");
printf("Chromosome X1 X2\n");
for(i=0; i<last_generation->n; i++){
printf(" %2d %6.2f ", i, last_generation->fitness[i]);
for(j=0; j<last_generation->chromosome->c_length; j++)
printf("%d",
last_generation->individual[i]->chromosome->allele[j]);
printf("%7.3f %6.3f\n",
last_generation->individual[i]->realPhenotype[0],
last_generation->individual[i]->realPhenotype[1]);
}
printf("\nMaximum: %6.2f for Individual %d\n",
last_generation->maxFitness,
last_generation->indexFittest);
printf("Minimum: %6.2f for Individual %d\n",
last_generation->minFitness,
last_generation->indexWeakest);
printf("Average: %6.2f\n", last_generation->avgFitness);
printf("Std. Dev: %6.2f\n\n", last_generation->stdFitness);
printf("%s\n", dashes);
}
/*********************************************************************/
/* De Jong's R2 Function */
/*********************************************************************/
static float deJongR2(Imsls_f_individual* individual)
{
float f, x1, x2;
x1 = individual->realPhenotype[0];
x2 = individual->realPhenotype[1];
f = 100*(x1*x1-x2)*(x1*x1-x2) + (1.0-x1)*(1.0-x1);
f = 4000 - f;
return f;
}
Output
In this example, the print level is set to IMSLS_FINAL in order to print the optimum solution. The generation statistics are requested using the IMSLS_GENERATIONS_STATS option, and the last population is requested using the IMSLS_LAST_GENERATION option.
Although the maximum number of generations is set to 100 using the IMSLS_GENERATIONS option, the genetic algorithm halted after 26 generations when the maximum population fitness exceeded 3999.999.
OPTIMUM SOLUTION
Fitness: 3999.999512
Phenotypes:
Real: 2
Function Calculations: 1080
Population Size: 40
Number of Generations: 26
Real Phenotype(s):
1.023594 1.047844
Chromosome (Gray Encoded):
11100000000001011010000111000011
*****************GENERATION STATISTICS*****************
Generation Max. Fit. Avg. Fit. Min. Fit. CV
*******************************************************
Gen. 0: 3996.12915 3244.16 578.91 28.62
Gen. 1: 3996.25269 3725.90 2770.41 8.24
Gen. 2: 3999.22974 3699.14 1917.26 10.28
Gen. 3: 3999.22974 3683.41 2551.70 9.87
Gen. 4: 3999.73779 3778.83 2551.70 8.35
Gen. 5: 3999.73779 3823.50 3187.72 5.22
Gen. 6: 3999.73779 3796.59 3187.72 5.76
Gen. 7: 3999.73779 3850.94 3302.26 4.28
Gen. 8: 3999.73779 3860.17 3358.92 3.93
Gen. 9: 3999.73779 3886.33 3138.96 4.23
Gen. 10: 3999.74683 3896.13 3292.64 3.85
Gen. 11: 3999.74683 3900.24 3638.17 2.93
Gen. 12: 3999.74683 3899.95 3376.35 3.17
Gen. 13: 3999.74683 3900.57 3476.12 3.19
Gen. 14: 3999.74683 3897.88 3408.28 3.36
Gen. 15: 3999.74683 3908.28 2331.26 3.36
Gen. 16: 3999.99585 3897.28 3301.18 3.94
Gen. 17: 3999.99585 3910.99 3236.92 3.31
Gen. 18: 3999.99585 3953.46 3429.17 1.31
Gen. 19: 3999.99585 3944.98 3764.08 1.41
Gen. 20: 3999.99585 3945.62 3751.01 1.41
Gen. 21: 3999.99585 3934.07 3751.10 1.81
Gen. 22: 3999.99585 3947.08 3739.52 1.62
Gen. 23: 3999.99609 3943.99 3652.86 1.95
Gen. 24: 3999.99609 3942.42 3652.86 1.99
Gen. 25: 3999.99927 3970.69 3845.42 0.92
Gen. 26: 3999.99951 3970.61 3845.42 0.90
LAST GENERATION
***************************************************************
Indv Fitness Chromosome X1 X2
0 3916.58 11100000000011001100110001010011 1.023 0.134
1 3996.09 01010000000001011100110001010011 -0.512 0.134
2 3965.22 11010000000011101110111110011011 0.511 0.849
3 3993.47 01100101000001011010000001100011 -0.928 1.028
4 3941.02 11010000000001011010000001100011 0.512 1.028
5 3998.11 11110000000001011100110001110011 0.512 0.134
6 3951.04 01100100000101011100110001100011 -0.898 0.132
7 3919.76 01000000000001011110110001110011 -0.000 0.890
8 3965.35 11110000000001011110111110011011 0.512 0.849
9 3913.56 11010000000011101010111101110011 0.511 1.190
10 3948.39 11010000000011101110001110110011 0.511 0.978
11 3996.04 01010000000001011100110001100011 -0.512 0.132
12 3997.44 11100000100111001110111101101001 1.009 0.859
13 3992.45 11110000000001110100000001000011 0.512 -0.008
14 3958.07 01010000000101011110110001110011 -0.510 0.890
15 3951.33 01100100000001011100110001100011 -0.896 0.132
16 3948.39 11010000000011101110001110110011 0.511 0.978
17 4000.00 11100000000001011010000111010001 1.024 1.046
18 3999.96 11100000000001011010000001100011 1.024 1.028
19 3925.31 01010110010001011010000111010001 -0.440 1.046
20 3999.37 11010000000001011101111001101111 0.512 0.325
21 3845.42 01100101010110110101110001100011 -0.921 -0.380
22 3999.64 11010101000011101100111001000011 0.415 0.184
23 3992.37 01100000000011101110111101101001 -1.023 0.859
24 3990.55 01010000000001110100000001110011 -0.512 -0.006
25 3993.26 11110000000011101100000001000011 0.513 0.008
26 3964.15 11010000000011101110111101110011 0.511 0.858
27 3998.36 11010000000011101100110010011011 0.511 0.143
28 3950.63 01100101000011101100111001000011 -0.927 0.184
29 3996.08 01010000000001011100110001110011 -0.512 0.134
30 3997.89 01010110000011101100111001100111 -0.447 0.188
31 3998.11 11110000000001011100110001110011 0.512 0.134
32 3993.47 01100101000001011010000001100011 -0.928 1.028
33 3992.45 11110000000001110100000001000011 0.512 -0.008
34 3916.61 11100000000011011100110001010011 1.023 0.134
35 3929.38 01010110000001011010000001100011 -0.448 1.028
36 3997.89 01010110000011101100111001100011 -0.447 0.188
37 4000.00 11100000000001011010000111010001 1.024 1.046
38 4000.00 11100000000001011010000111000011 1.024 1.048
39 3991.28 01100100000001011010000001110001 -0.896 1.030
Maximum: 4000.00 for Individual 38
Minimum: 3845.42 for Individual 21
Average: 3970.61
Std. Dev: 35.71
Example 2
The traveling saleman problem creates a problem for traditional crossover. In this problem, the objective is to find the shortest route while traveling to each city once. In this example, there are eight cities, labeled using the letters a-h, with distances ranging from 17 to 113 miles.
Traditional crossover would create unfeasible routes; that is some routes after crossover would not visit every city once. Some would not be visited and others would be visited more than once.
Partially matched crossover (PMX) preserves the feasibility of a route. In the general sense, PMX assumes that the nominal phenotypes consists of a string of numbers from zero to n_nominal-1, with each number appearing once and only once in that string. Partially matched crossover uses two crossover points within the nominal portion of the chromosome and swaps the middle segment between the parents. The first and third segments are manipulated to ensure the resulting offspring is feasible.
#include <imsls.h>
#include <stdio.h>
#include <stdlib.h>
int main(){
int i, j, k; /* index variables */
int n = 50; /* population size */
int n_generations; /* number of generations */
int n_nominal = 8; /* number of nominal phenotypes*/
int n_categories[8] = {8, 8, 8, 8,
8, 8, 8, 8}; /* nominal category limits */
float x1; /* temporary storage */
float avg; /* average fitness */
float* genStats; /* generation statistics */
static float pmxFitness(Imsls_f_individual* individual);
Imsls_f_chromosome* chromosome; /* chromosome data structure */
Imsls_f_individual* best_individual;/* optimum */
Imsls_f_population* population; /* population data structure */
Imsls_f_population* last_generation;/* last generation */
char *cities[8] = {"a", "b", "c", "d", /* Cities Label a-h */
"e", "f", "g", "h"};
/*******************************************************************/
/* In this example the user function is thread safe. Let CNL */
/* know it is safe, which allows genetic algorithm to run in */
/* parallel, if that capability exists on the user computer. */
imsls_omp_options(
IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1,
0);
imsls_random_seed_set(12345);
chromosome = imsls_f_ga_chromosome(
IMSLS_NOMINAL, n_nominal, n_categories,
0);
population = imsls_f_ga_random_population(n, chromosome,
IMSLS_PMX_CROSSOVER,
IMSLS_FITNESS_FCN, pmxFitness,
0);
best_individual = imsls_f_genetic_algorithm(pmxFitness, population,
IMSLS_PRINT_LEVEL, IMSLS_FINAL,
IMSLS_PMX_CROSSOVER,
IMSLS_INVERT_CROSSOVER,
IMSLS_CROSSOVER_PROB, 0.8,
IMSLS_MAX_GENERATIONS, 10,
IMSLS_GENERATION_STATS, &genStats,
IMSLS_N_GENERATIONS, &n_generations,
IMSLS_LAST_GENERATION, &last_generation,
0);
printf("GENERATION STATISTICS\n");
printf("Total Number of Generations: %d\n\n", n_generations);
printf("Generation Max. Fit. Min. Fit. Avg. Fit. CV\n");
for(i=0; i<=n_generations; i++){
printf("Gen. %3d: %8.0f %8.0f %12.2f %8.2f\n",
i, genStats[4*i], genStats[4*i+1], genStats[4*i+2],
100*genStats[4*i+3]/genStats[4*i+2]);
}
printf("\n\n LAST GENERATION\n");
printf("*************************************\n");
printf("Individual Fitness Phenotype Values \n");
avg = last_generation->avgFitness;
for(i=0; i<last_generation->n; i++){
x1 = last_generation->fitness[i];
printf(" %2d %6.0f ", i, x1);
for(j=0; j<last_generation->chromosome->c_length; j++) {
k = last_generation->individual[i]->nominalPhenotype[j];
printf("%s ", cities[k]);
}
if(x1 == last_generation->maxFitness){
printf("***\n");
}else{
printf("\n");
}
}
printf("Average Fitness: %6.1f\n\n", avg);
printf("*************************************\n");
printf("OPTIMUM SOLUTION:\n\nFitness:%4.0f\n\nChromosome: ",
pmxFitness(best_individual));
for(i=0; i<best_individual->chromosome->c_length; i++)
printf("%3d", best_individual->chromosome->allele[i]);
printf("\n\nPhenotype Values: ");
for(i=0; i<n_nominal; i++) {
k = best_individual->nominalPhenotype[i];
printf("->%s", cities[k]);
}
printf("\n\n");
printf("freeing best individual\n");
imsls_f_ga_free_individual(best_individual);
printf("freeing last generation\n");
imsls_f_ga_free_population(last_generation);
printf("freeing chromosome\n");
free(chromosome);
printf("freeing population\n");
imsls_f_ga_free_population(population);
system("pause");
}
/***********************************************************************/
/* FITNESS FUNCTION */
/********************************************************************* */
static float pmxFitness(Imsls_f_individual* individual)
{
int i=0, k=0, i1, i2; /* Index variables */
int n_nominal = 8; /* number of nominal phenotypes */
float f = 0.0; /* fitness value */
/* cities: a b c d e f g h */
float distances[64] = { 0, 17, 27, 73, 61, 57, 51, 23, /* a */
17, 0, 37, 73, 72, 74, 66, 40, /* b */
27, 37, 0, 48, 35, 49, 65, 50, /* c */
73, 73, 48, 0, 47, 82, 113, 95, /* d */
61, 72, 35, 47, 0, 38, 80, 78, /* e */
57, 74, 49, 82, 38, 0, 48, 65, /* f */
51, 66, 65, 113, 80, 48, 0, 40, /* g */
23, 40, 50, 95, 78, 65, 40, 0};/* h */
n_nominal = individual->chromosome->n_nominal;
k = individual->chromosome->nominalIndex+1;
f = 0.0;
for(i=k; i<k+n_nominal-1; i++){
i1 = individual->nominalPhenotype[i-1];
i2 = individual->nominalPhenotype[i ];
f += distances[i1*n_nominal + i2];
}
return 516-f;
}
Output
This program produced the following output. Since the print level was set to IMSLS_FINAL, the optimum solution was printed. The generation statistics were requested using the IMSLS_GENERATIONS_STATS option, and the last population was requested using the IMSLS_LAST_GENERATION option.
The maximum number of generations was set to 10. The genetic algorithm found the optimum route after evaluating the fitness of 550 routes in 10 generations. Generation zero is the initial generation provided to the algorithm and is not counted towards the maximum generation count.
OPTIMUM SOLUTION
Fitness: 269.000000
Phenotypes:
Nominal: 8
Function Calculations: 550
Population Size: 50
Number of Generations: 10
Nominal Phenotype(s):
3 4 2 1 0 7 6 5
Chromosome (Base-2 Encoded):
3 4 2 1 0 7 6 5
GENERATION STATISTICS
Total Number of Generations: 10
Generation Max. Fit. Min. Fit. Avg. Fit. CV
Gen. 0: 194 29 113.64 33.55
Gen. 1: 251 24 119.10 35.08
Gen. 2: 251 37 131.16 35.99
Gen. 3: 251 38 128.96 33.68
Gen. 4: 251 29 135.08 33.25
Gen. 5: 255 38 136.18 33.44
Gen. 6: 255 28 142.38 33.23
Gen. 7: 255 56 150.56 29.31
Gen. 8: 269 55 155.06 28.88
Gen. 9: 269 56 148.62 26.68
Gen. 10: 269 48 146.32 29.59
LAST GENERATION
*************************************
Individual Fitness Phenotype Values
0 106 a c d g b h e f
1 269 d e c b a h g f ***
2 222 d e c h g f a b
3 154 e a g h b d c f
4 215 e d c a b f g h
5 215 e d c a b f g h
6 158 a h b c d f g e
7 113 c a d b f e h g
8 78 f a d b h c g e
9 125 e d h g b c f a
10 118 c b e g f h a d
11 209 d e c b h g a f
12 161 h b a d c f g e
13 167 g d b a h c e f
14 169 a f h g b c e d
15 137 f g a e d h b c
16 127 h d a b c f e g
17 90 b d h g c e a f
18 216 d h b a c e f g
19 167 g d e c f h a b
20 120 e h f c d a b g
21 86 f a h d b c g e
22 171 a b d f g h c e
23 156 d h g a c e f b
24 146 c e a d b h g f
25 116 f d g e c h a b
26 118 b c a h e f d g
27 95 d g a b f e h c
28 143 d h b a f c e g
29 157 b f c g h a e d
30 175 b e a h g f c d
31 146 c e a d b h g f
32 111 c b e h g f a d
33 140 b e a f g h c d
34 164 b c e d g h a f
35 166 f e b c a h g d
36 199 b a g h f c d e
37 171 e d f a b c g h
38 97 f a c d h b e g
39 222 d e c h g f a b
40 128 d h c g a b e f
41 99 e g d c b a f h
42 112 d h f c b a e g
43 107 h d a b e f c g
44 143 c h a b f d e g
45 144 g a c e d b f h
46 64 a e c g h d f b
47 103 b d f h g c a e
48 129 d a g b f e c h
49 172 f h b g a c d e
Average Fitness: 146.3
*************************************
OPTIMUM SOLUTION:
Fitness: 269
Chromosome: 3 4 2 1 0 7 6 5
Phenotype Values: ->d->e->c->b->a->h->g->f
freeing best individual
freeing last generation
freeing chromosome
freeing population
Example 3
This example uses the N-Queens problem to illustrate the use of a fitness function with parameters in implementing a genetic algorithm. The N-Queens problem is derived from chess. The genetic algorithm provides an efficient search for a valid solution. For this problem the chess board consists of N rows and N columns. The objective is to place N queens on this board with no conflicts. A conflict occurs when one queen can move and capture another. Since queens can move diagonally, vertically and horizontally this problem is challenging when N becomes large.
One solution for N = 4 is displayed in the following table. A valid solution must place every queen in a different row and column. The problem is to ensure the queens are not in conflict because of lying on the same diagonal.
|
Row/Col |
0 |
1 |
2 |
3 |
|
0 |
|
|
Q |
|
|
1 |
Q |
|
|
|
|
2 |
|
|
|
Q |
|
3 |
|
Q |
|
|
Similar to the traveling salesman problem, the N-Queens problem can be expressed using N nominal phenotypes with values 0, 1, …, N-1. The value of the i-th phenotype represents the row number for the queen in the i-th column. This ensures that any arrangement of the phenotype values represents a board with N queens, each placed in a different row and column.
The solution for N queens displayed above can be represented by the phenotype values {1, 3, 0, 2}. The search looks for arrangements that also do not place queens on the same diagonal. Two queens fall on the same diagonal if the absolute value of the difference between their row numbers equals the absolute value of the difference between their column numbers.
This example uses this representation with a fitness function equal to (N – C) where C equals the number of conflict among the queens. With this fitness, a solution to the N-Queens has a fitness of N.
#include <imsls.h>
#include <imsls.h>
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
typedef struct
{
int n_queens;
} inputArgs;
int main(){
int i, j, k; /* index variables */
int n = 500; /* population size */
int n_generations; /* number of generations */
int n_queens = 25; /* number of nominal phenotypes*/
int n_categories[25];
float maxFit; /* maximum fitness hurdle */
float* genStats; /* generation statistics */
static float queensFitness(
Imsls_f_individual* individual, inputArgs* input);
inputArgs* parameters;
Imsls_f_chromosome* chromosome; /* chromosome */
Imsls_f_individual* best_individual;/* optimum */
Imsls_f_population* population; /* population */
/**************************************************/
/* In this example the user function is thread */
/* safe. Let CNL know it is safe, which allows *
/* genetic algorithm to run in parallel, if that */
/* capability exists on the user computer. */
imsls_omp_options(IMSLS_SET_FUNCTIONS_THREAD_SAFE, 1, 0);
imsls_random_seed_set(12345);
maxFit = n_queens - 0.5;
for(i=0; i<n_queens; i++) n_categories[i] = n_queens;
chromosome = imsls_f_ga_chromosome(
IMSLS_NOMINAL, n_queens, n_categories, 0);
parameters = (inputArgs*) malloc(sizeof(inputArgs));
parameters->n_queens = n_queens;
population = imsls_f_ga_random_population(n,
chromosome,
IMSLS_PMX_CROSSOVER,
IMSLS_FITNESS_FCN_WITH_PARMS,
queensFitness, parameters, 0);
best_individual = imsls_f_genetic_algorithm(
NULL, population,
IMSLS_FITNESS_FCN_WITH_PARMS, queensFitness, parameters,
IMSLS_PRINT_LEVEL, IMSLS_FINAL,
IMSLS_PMX_CROSSOVER,
IMSLS_LINEAR_SCALING, 2.0,
IMSLS_CROSSOVER_PROB, 0.7,
IMSLS_MUTATION_PROB, 0.01,
IMSLS_MAX_GENERATIONS, 10000,
IMSLS_MAX_FITNESS, maxFit,
IMSLS_GENERATION_STATS, &genStats,
IMSLS_N_GENERATIONS, &n_generations, 0);
printf("GENERATION STATISTICS\n");
printf("Total Number of Generations: %d\n\n", n_generations);
printf("Generation Max. Fit. Min. Fit. Avg. Fit. CV\n");
printf("*************************************************\n");
for(i=0; i<=n_generations; i+=25){
printf("Gen. %3d: %8.0f %8.0f %12.2f %8.2f\n",
i, genStats[4*i], genStats[4*i+1], genStats[4*i+2],
100*genStats[4*i+3]/genStats[4*i+2]);
}
i = n_generations;
printf("Gen. %3d: %8.0f %8.0f %12.2f %8.2f\n",
i, genStats[4*i], genStats[4*i+1], genStats[4*i+2],
100*genStats[4*i+3]/genStats[4*i+2]);
printf("*************************************************\n");
printf("OPTIMUM SOLUTION:\n\nFitness:%4.0f\n\nChromosome: ",
queensFitness(best_individual, parameters));
for(i=0; i<best_individual->chromosome->c_length; i++)
printf("%3d", best_individual->chromosome->allele[i]);
if(n_queens<100){
printf("\n\nBoard Positions: \n\n");
for(i=0; i<n_queens; i++) printf("--");
printf("-\n");
for(i=0; i<n_queens; i++) {
for(j=0; j<n_queens; j++){
k = best_individual->nominalPhenotype[j];
if(i==k) printf("|Q");
else printf("| ");
}
printf("|\n");
for(k=0; k<n_queens; k++) printf("--");
printf("-\n");
}
printf("\n\n");
}
}
static float queensFitness(Imsls_f_individual* individual, inputArgs* input)
{
int i=0, j=0, k=0; /* Index variables */
int n_queens;
float f = 0.0; /* Fitness value */
n_queens = input->n_queens;
f = 0;
for(i=0; i<n_queens-1; i++){
for(j=i+1; j<n_queens; j++){
k = individual->chromosome->allele[i] -
individual->chromosome->allele[j] ;
k = abs(k);
if (abs(i-j) == k) f++;
}
}
f = n_queens - f;
return f;
}
Output
This program produced the following solution to the N-Queens problem with N=50 queens. Notice that some of the minimum fitness values are negative. This alters the random selection of the fittest parents, but if these values are few and small, then the effect is not enough to halt the genetic algorithm.
For 50 queens there are over 1064 ways of placing queens ensuring each is in its own row and column. An exhaustive search of these possible solutions to find a arrangement without diagonal conflicts would be time consuming. The genetic algorithm search found a solution in only 568 generations, requiring 284,500 function evaluations.
OPTIMUM SOLUTION
Fitness: 25.000000
Phenotypes:
Nominal: 25
Function Calculations: 284500
Population Size: 500
Number of Generations: 568
Nominal Phenotype(s):
23 12 16 9 13 2 18 1 21 10 6 19
3 20 0 7 15 4 8 17 22 14 5 11
24
Chromosome (Base-2 Encoded):
23 12 16 9 13 2 18 1 21 10 6 19 3 20 0 7 15 4
8 17 22 14 5 11 24
GENERATION STATISTICS
Total Number of Generations: 568
Generation Max. Fit. Min. Fit. Avg. Fit. CV
*************************************************
Gen. 0: 19 -10 8.11 52.98
Gen. 25: 21 -2 11.02 30.33
Gen. 50: 21 -4 11.49 29.48
Gen. 75: 21 -1 11.15 29.51
Gen. 100: 21 -3 11.42 33.10
Gen. 125: 21 -3 11.17 31.50
Gen. 150: 21 -4 10.64 34.01
Gen. 175: 21 -8 10.60 34.64
Gen. 200: 21 -4 11.16 32.47
Gen. 225: 21 -2 10.76 34.18
Gen. 250: 22 -1 11.08 32.50
Gen. 275: 22 -4 10.98 34.14
Gen. 300: 23 -3 10.97 33.84
Gen. 325: 23 -1 11.75 29.37
Gen. 350: 23 -10 11.08 33.76
Gen. 375: 23 -4 11.54 31.17
Gen. 400: 23 1 11.55 30.43
Gen. 425: 23 -8 12.76 26.36
Gen. 450: 23 -2 12.01 27.39
Gen. 475: 23 0 12.94 27.34
Gen. 500: 23 3 13.78 22.91
Gen. 525: 23 4 15.05 17.90
Gen. 550: 24 4 16.47 18.41
Gen. 568: 25 12 19.48 11.63
*************************************************
OPTIMUM SOLUTION:
Fitness: 25
Chromosome: 23 12 16 9 13 2 18 1 21 10 6 19 3 20
0 7 15 4 8 17 22 14 5 11 24
Board Positions:
---------------------------------------------------
| | | | | | | | | | | | | | |Q| | | | | | | | | | |
---------------------------------------------------
| | | | | | | |Q| | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | |Q| | | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | |Q| | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | |Q| | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | | | | | |Q| | |
---------------------------------------------------
| | | | | | | | | | |Q| | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | |Q| | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | |Q| | | | | | |
---------------------------------------------------
| | | |Q| | | | | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | |Q| | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | | | | | | |Q| |
---------------------------------------------------
| |Q| | | | | | | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | |Q| | | | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | | | | |Q| | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | |Q| | | | | | | | |
---------------------------------------------------
| | |Q| | | | | | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | | |Q| | | | | |
---------------------------------------------------
| | | | | | |Q| | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | |Q| | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | |Q| | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | |Q| | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | | | |Q| | | | |
---------------------------------------------------
|Q| | | | | | | | | | | | | | | | | | | | | | | | |
---------------------------------------------------
| | | | | | | | | | | | | | | | | | | | | | | | |Q|
----------------------------------------------------

